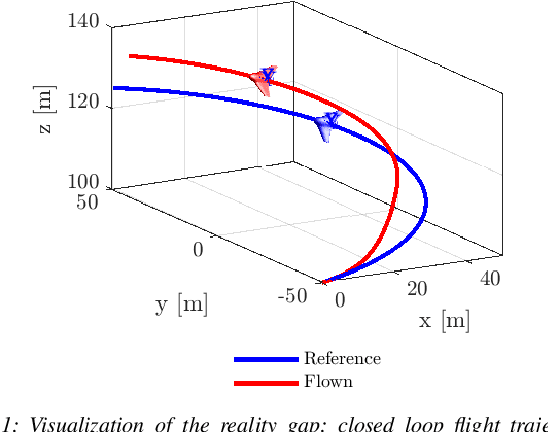
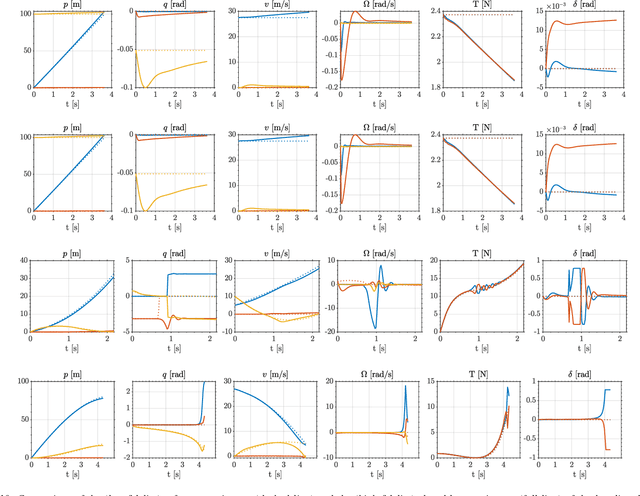
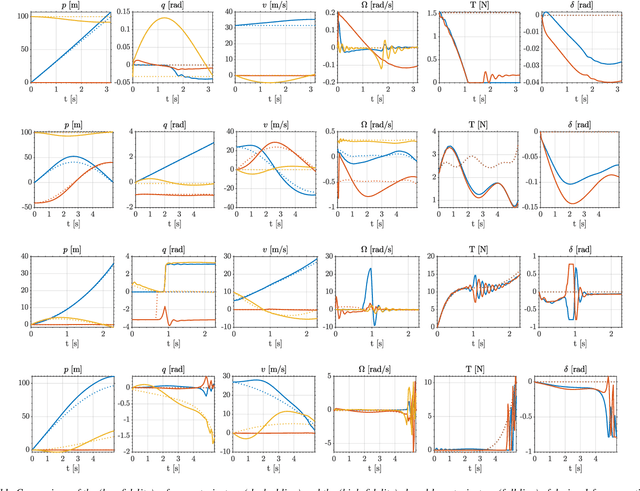
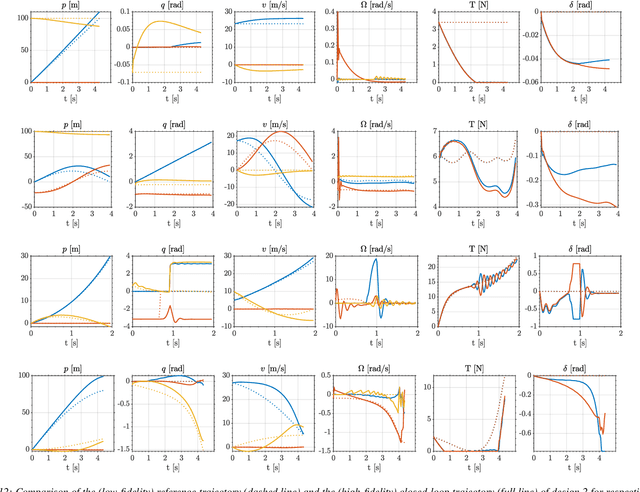
Introducing DAIMYO: a first-time-right dynamic design architecture and its application to tail-sitter UAS development

In recent years, there has been a notable evolution in various multidisciplinary design methodologies for dynamic systems. Among these approaches, a noteworthy concept is that of concurrent conceptual and control design or co-design. This approach involves the tuning of feedforward and/or feedback control strategies in conjunction with the conceptual design of the dynamic system. The primary aim is to discover integrated solutions that surpass those attainable through a disjointed or decoupled approach. This concurrent design paradigm exhibits particular promise in the context of hybrid unmanned aerial systems (UASs), such as tail-sitters, where the objectives of versatility (driven by control considerations) and efficiency (influenced by conceptual design) often present conflicting demands. Nevertheless, a persistent challenge lies in the potential disparity between the theoretical models that underpin the design process and the real-world operational environment, the so-called reality gap. Such disparities can lead to suboptimal performance when the designed system is deployed in reality. To address this issue, this paper introduces DAIMYO, a novel design architecture that incorporates a high-fidelity environment, which emulates real-world conditions, into the procedure in pursuit of a `first-time-right' design. The outcome of this innovative approach is a design procedure that yields versatile and efficient UAS designs capable of withstanding the challenges posed by the reality gap.

Deterministic Trajectory Optimization through Probabilistic Optimal Control

This article proposes two new algorithms tailored to discrete-time deterministic finite-horizon nonlinear optimal control problems or so-called trajectory optimization problems. Both algorithms are inspired by a novel theoretical paradigm known as probabilistic optimal control, that reformulates optimal control as an equivalent probabilistic inference problem. This perspective allows to address the problem using the Expectation-Maximization algorithm. We show that the application of this algorithm results in a fixed point iteration of probabilistic policies that converge to the deterministic optimal policy. Two strategies for policy evaluation are discussed, using state-of-the-art uncertainty quantification methods resulting into two distinct algorithms. The algorithms are structurally closest related to the differential dynamic programming algorithm and related methods that use sigma-point methods to avoid direct gradient evaluations. The main advantage of our work is an improved balance between exploration and exploitation over the iterations, leading to improved numerical stability and accelerated convergence. These properties are demonstrated on different nonlinear systems.

Variational Inference for SDEs Driven by Fractional Noise

We present a novel variational framework for performing inference in (neural) stochastic differential equations (SDEs) driven by Markov-approximate fractional Brownian motion (fBM). SDEs offer a versatile tool for modeling real-world continuous-time dynamic systems with inherent noise and randomness. Combining SDEs with the powerful inference capabilities of variational methods, enables the learning of representative function distributions through stochastic gradient descent. However, conventional SDEs typically assume the underlying noise to follow a Brownian motion (BM), which hinders their ability to capture long-term dependencies. In contrast, fractional Brownian motion (fBM) extends BM to encompass non-Markovian dynamics, but existing methods for inferring fBM parameters are either computationally demanding or statistically inefficient. In this paper, building upon the Markov approximation of fBM, we derive the evidence lower bound essential for efficient variational inference of posterior path measures, drawing from the well-established field of stochastic analysis. Additionally, we provide a closed-form expression to determine optimal approximation coefficients. Furthermore, we propose the use of neural networks to learn the drift, diffusion and control terms within our variational posterior, leading to the variational training of neural-SDEs. In this framework, we also optimize the Hurst index, governing the nature of our fractional noise. Beyond validation on synthetic data, we contribute a novel architecture for variational latent video prediction,-an approach that, to the best of our knowledge, enables the first variational neural-SDE application to video perception.

A Supervisory Learning Control Framework for Autonomous & Real-time Task Planning for an Underactuated Cooperative Robotic task

We introduce a framework for cooperative manipulation, applied on an underactuated manipulation problem. Two stationary robotic manipulators are required to cooperate in order to reposition an object within their shared work space. Control of multi-agent systems for manipulation tasks cannot rely on individual control strategies with little to no communication between the agents that serve the common objective through swarming. Instead a coordination strategy is required that queries subtasks to the individual agents. We formulate the problem in a Task And Motion Planning (TAMP) setting, while considering a decomposition strategy that allows us to treat the task and motion planning problems separately. We solve the supervisory planning problem offline using deep Reinforcement Learning techniques resulting into a supervisory policy capable of coordinating the two manipulators into a successful execution of the pick-and-place task. Additionally, a benefit of solving the task planning problem offline is the possibility of real-time (re)planning, demonstrating robustness in the event of subtask execution failure or on-the-fly task changes. The framework achieved zero-shot deployment on the real setup with a success rate that is higher than 90%.

KeyCLD: Learning Constrained Lagrangian Dynamics in Keypoint Coordinates from Images

We present KeyCLD, a framework to learn Lagrangian dynamics from images. Learned keypoints represent semantic landmarks in images and can directly represent state dynamics. Interpreting this state as Cartesian coordinates coupled with explicit holonomic constraints, allows expressing the dynamics with a constrained Lagrangian. Our method explicitly models kinetic and potential energy, thus allowing energy based control. We are the first to demonstrate learning of Lagrangian dynamics from images on the dm_control pendulum, cartpole and acrobot environments. This is a step forward towards learning Lagrangian dynamics from real-world images, since previous work in literature was only applied to minimalistic images with monochromatic shapes on empty backgrounds. Please refer to our project page for code and additional results: https://rdaems.github.io/keycld/

Entropy Regularised Deterministic Optimal Control: From Path Integral Solution to Sample-Based Trajectory Optimisation

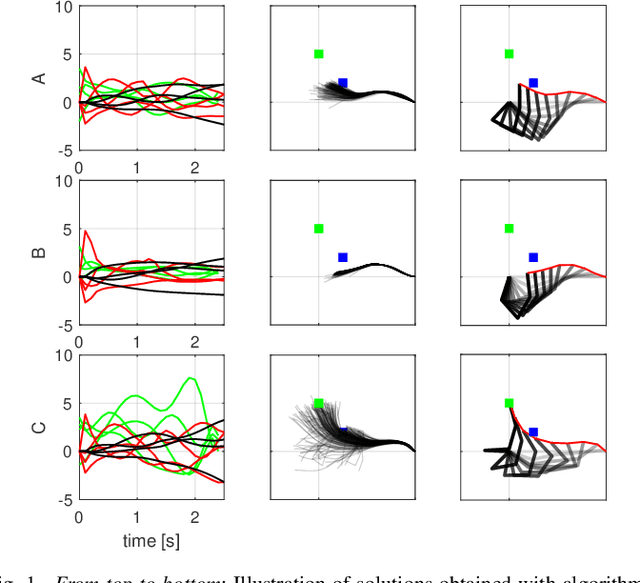
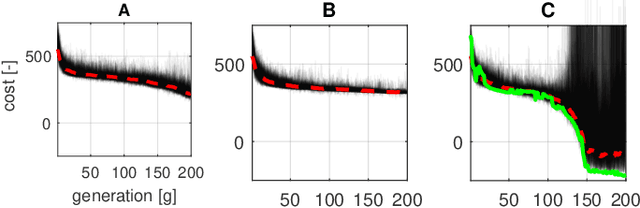
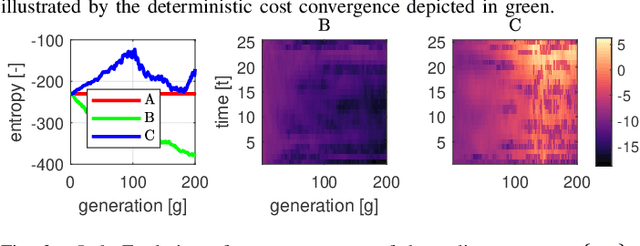
Sample-based trajectory optimisers are a promising tool for the control of robotics with non-differentiable dynamics and cost functions. Contemporary approaches derive from a restricted subclass of stochastic optimal control where the optimal policy can be expressed in terms of an expectation over stochastic paths. By estimating the expectation with Monte Carlo sampling and reinterpreting the process as exploration noise, a stochastic search algorithm is obtained tailored to (deterministic) trajectory optimisation. For the purpose of future algorithmic development, it is essential to properly understand the underlying theoretical foundations that allow for a principled derivation of such methods. In this paper we make a connection between entropy regularisation in optimisation and deterministic optimal control. We then show that the optimal policy is given by a belief function rather than a deterministic function. The policy belief is governed by a Bayesian-type update where the likelihood can be expressed in terms of a conditional expectation over paths induced by a prior policy. Our theoretical investigation firmly roots sample based trajectory optimisation in the larger family of control as inference. It allows us to justify a number of heuristics that are common in the literature and motivate a number of new improvements that benefit convergence.

Adaptive control of a mechatronic system using constrained residual reinforcement learning

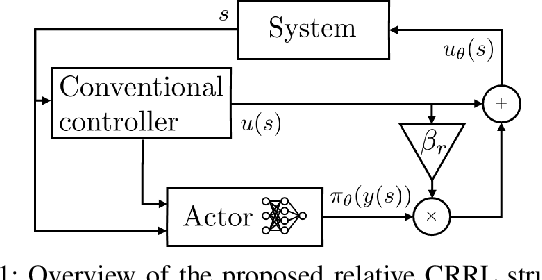
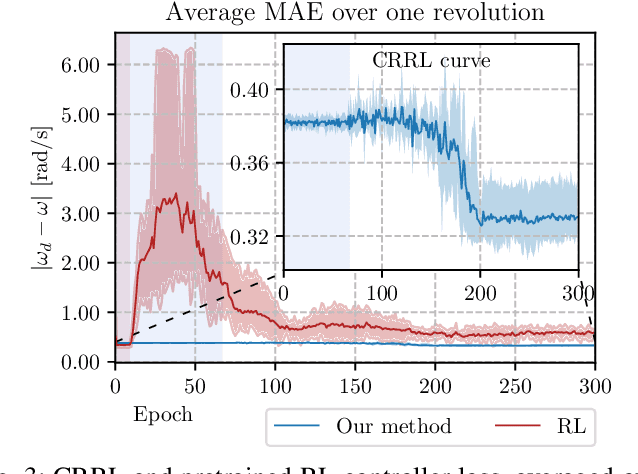
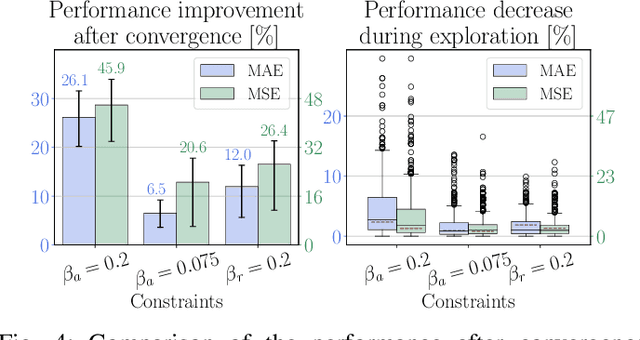
We propose a simple, practical and intuitive approach to improve the performance of a conventional controller in uncertain environments using deep reinforcement learning while maintaining safe operation. Our approach is motivated by the observation that conventional controllers in industrial motion control value robustness over adaptivity to deal with different operating conditions and are suboptimal as a consequence. Reinforcement learning on the other hand can optimize a control signal directly from input-output data and thus adapt to operational conditions, but lacks safety guarantees, impeding its use in industrial environments. To realize adaptive control using reinforcement learning in such conditions, we follow a residual learning methodology, where a reinforcement learning algorithm learns corrective adaptations to a base controller's output to increase optimality. We investigate how constraining the residual agent's actions enables to leverage the base controller's robustness to guarantee safe operation. We detail the algorithmic design and propose to constrain the residual actions relative to the base controller to increase the method's robustness. Building on Lyapunov stability theory, we prove stability for a broad class of mechatronic closed-loop systems. We validate our method experimentally on a slider-crank setup and investigate how the constraints affect the safety during learning and optimality after convergence.