Entropy Regularised Deterministic Optimal Control: From Path Integral Solution to Sample-Based Trajectory Optimisation
Paper and Code
Oct 06, 2021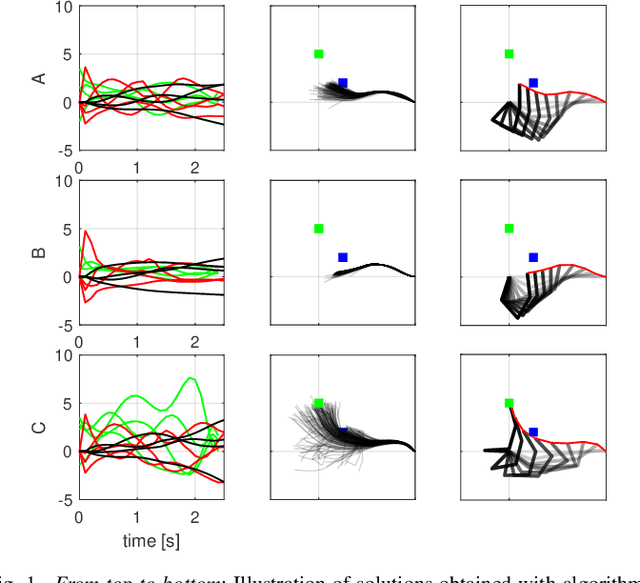
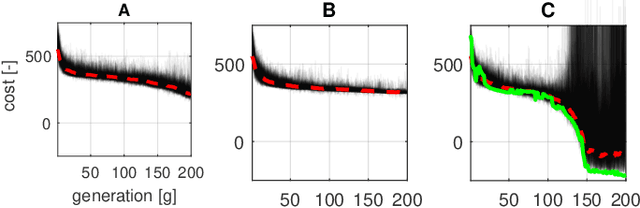
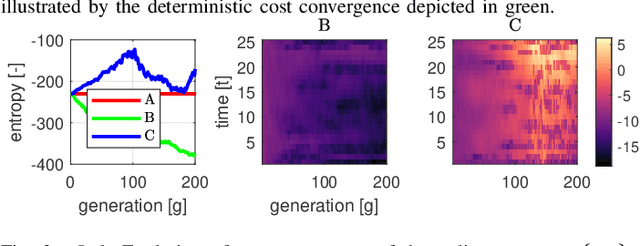
Sample-based trajectory optimisers are a promising tool for the control of robotics with non-differentiable dynamics and cost functions. Contemporary approaches derive from a restricted subclass of stochastic optimal control where the optimal policy can be expressed in terms of an expectation over stochastic paths. By estimating the expectation with Monte Carlo sampling and reinterpreting the process as exploration noise, a stochastic search algorithm is obtained tailored to (deterministic) trajectory optimisation. For the purpose of future algorithmic development, it is essential to properly understand the underlying theoretical foundations that allow for a principled derivation of such methods. In this paper we make a connection between entropy regularisation in optimisation and deterministic optimal control. We then show that the optimal policy is given by a belief function rather than a deterministic function. The policy belief is governed by a Bayesian-type update where the likelihood can be expressed in terms of a conditional expectation over paths induced by a prior policy. Our theoretical investigation firmly roots sample based trajectory optimisation in the larger family of control as inference. It allows us to justify a number of heuristics that are common in the literature and motivate a number of new improvements that benefit convergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge