Efficient Training of Neural SDEs Using Stochastic Optimal Control

We present a hierarchical, control theory inspired method for variational inference (VI) for neural stochastic differential equations (SDEs). While VI for neural SDEs is a promising avenue for uncertainty-aware reasoning in time-series, it is computationally challenging due to the iterative nature of maximizing the ELBO. In this work, we propose to decompose the control term into linear and residual non-linear components and derive an optimal control term for linear SDEs, using stochastic optimal control. Modeling the non-linear component by a neural network, we show how to efficiently train neural SDEs without sacrificing their expressive power. Since the linear part of the control term is optimal and does not need to be learned, the training is initialized at a lower cost and we observe faster convergence.

Inferring Parameter Distributions in Heterogeneous Motile Particle Ensembles: A Likelihood Approach for Second Order Langevin Models

The inherent complexity of biological agents often leads to motility behavior that appears to have random components. Robust stochastic inference methods are therefore required to understand and predict the motion patterns from time discrete trajectory data provided by experiments. In many cases second order Langevin models are needed to adequately capture the motility. Additionally, population heterogeneity needs to be taken into account when analyzing data from several individual organisms. In this work, we describe a maximum likelihood approach to infer dynamical, stochastic models and, simultaneously, estimate the heterogeneity in a population of motile active particles from discretely sampled, stochastic trajectories. To this end we propose a new method to approximate the likelihood for non-linear second order Langevin models. We show that this maximum likelihood ansatz outperforms alternative approaches especially for short trajectories. Additionally, we demonstrate how a measure of uncertainty for the heterogeneity estimate can be derived. We thereby pave the way for the systematic, data-driven inference of dynamical models for actively driven entities based on trajectory data, deciphering temporal fluctuations and inter-particle variability.

Bridging discrete and continuous state spaces: Exploring the Ehrenfest process in time-continuous diffusion models

Generative modeling via stochastic processes has led to remarkable empirical results as well as to recent advances in their theoretical understanding. In principle, both space and time of the processes can be discrete or continuous. In this work, we study time-continuous Markov jump processes on discrete state spaces and investigate their correspondence to state-continuous diffusion processes given by SDEs. In particular, we revisit the $\textit{Ehrenfest process}$, which converges to an Ornstein-Uhlenbeck process in the infinite state space limit. Likewise, we can show that the time-reversal of the Ehrenfest process converges to the time-reversed Ornstein-Uhlenbeck process. This observation bridges discrete and continuous state spaces and allows to carry over methods from one to the respective other setting. Additionally, we suggest an algorithm for training the time-reversal of Markov jump processes which relies on conditional expectations and can thus be directly related to denoising score matching. We demonstrate our methods in multiple convincing numerical experiments.

A Convergence Analysis of Approximate Message Passing with Non-Separable Functions and Applications to Multi-Class Classification

Motivated by the recent application of approximate message passing (AMP) to the analysis of convex optimizations in multi-class classifications [Loureiro, et. al., 2021], we present a convergence analysis of AMP dynamics with non-separable multivariate nonlinearities. As an application, we present a complete (and independent) analysis of the motivated convex optimization problem.

Variational Inference for SDEs Driven by Fractional Noise

We present a novel variational framework for performing inference in (neural) stochastic differential equations (SDEs) driven by Markov-approximate fractional Brownian motion (fBM). SDEs offer a versatile tool for modeling real-world continuous-time dynamic systems with inherent noise and randomness. Combining SDEs with the powerful inference capabilities of variational methods, enables the learning of representative function distributions through stochastic gradient descent. However, conventional SDEs typically assume the underlying noise to follow a Brownian motion (BM), which hinders their ability to capture long-term dependencies. In contrast, fractional Brownian motion (fBM) extends BM to encompass non-Markovian dynamics, but existing methods for inferring fBM parameters are either computationally demanding or statistically inefficient. In this paper, building upon the Markov approximation of fBM, we derive the evidence lower bound essential for efficient variational inference of posterior path measures, drawing from the well-established field of stochastic analysis. Additionally, we provide a closed-form expression to determine optimal approximation coefficients. Furthermore, we propose the use of neural networks to learn the drift, diffusion and control terms within our variational posterior, leading to the variational training of neural-SDEs. In this framework, we also optimize the Hurst index, governing the nature of our fractional noise. Beyond validation on synthetic data, we contribute a novel architecture for variational latent video prediction,-an approach that, to the best of our knowledge, enables the first variational neural-SDE application to video perception.

Analysis of Random Sequential Message Passing Algorithms for Approximate Inference

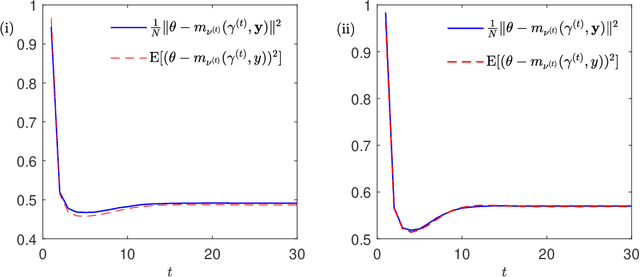
We analyze the dynamics of a random sequential message passing algorithm for approximate inference with large Gaussian latent variable models in a student-teacher scenario. To model nontrivial dependencies between the latent variables, we assume random covariance matrices drawn from rotation invariant ensembles. Moreover, we consider a model mismatching setting, where the teacher model and the one used by the student may be different. By means of dynamical functional approach, we obtain exact dynamical mean-field equations characterizing the dynamics of the inference algorithm. We also derive a range of model parameters for which the sequential algorithm does not converge. The boundary of this parameter range coincides with the de Almeida Thouless (AT) stability condition of the replica symmetric ansatz for the static probabilistic model.

Adaptive Inducing Points Selection For Gaussian Processes

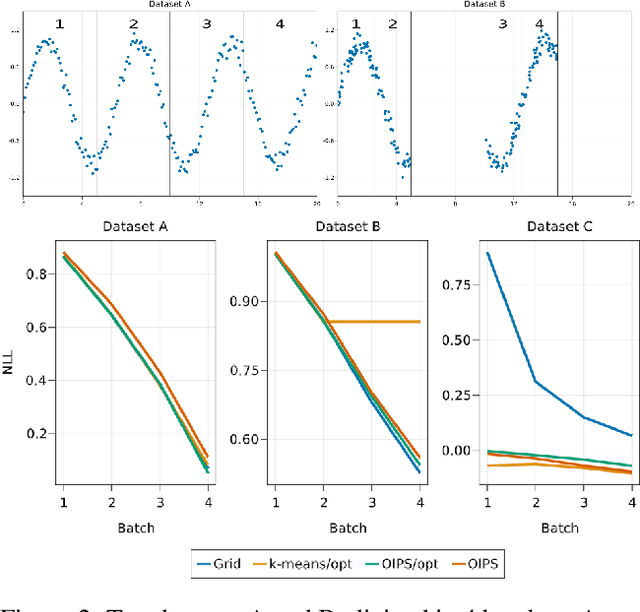
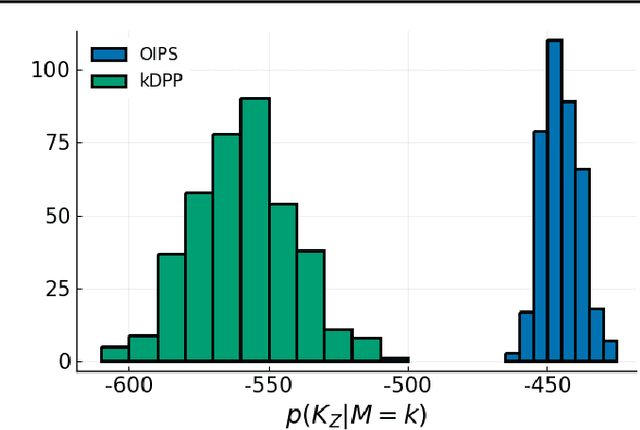
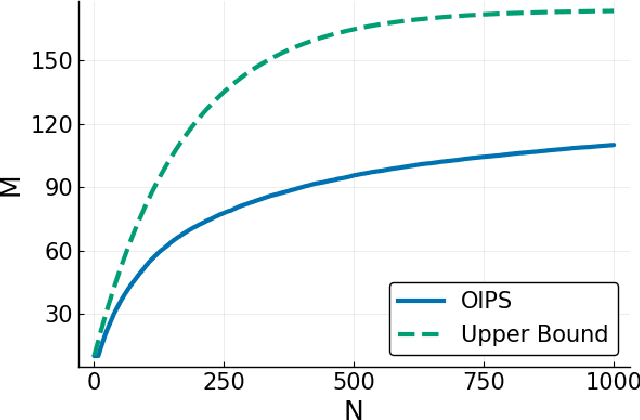
Gaussian Processes (\textbf{GPs}) are flexible non-parametric models with strong probabilistic interpretation. While being a standard choice for performing inference on time series, GPs have few techniques to work in a streaming setting. \cite{bui2017streaming} developed an efficient variational approach to train online GPs by using sparsity techniques: The whole set of observations is approximated by a smaller set of inducing points (\textbf{IPs}) and moved around with new data. Both the number and the locations of the IPs will affect greatly the performance of the algorithm. In addition to optimizing their locations, we propose to adaptively add new points, based on the properties of the GP and the structure of the data.

Nonlinear Hawkes Process with Gaussian Process Self Effects

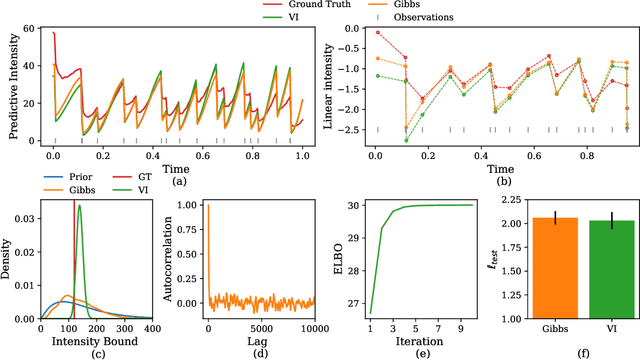
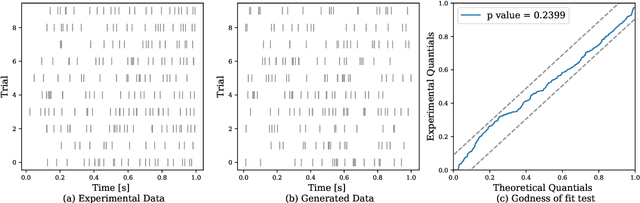
Traditionally, Hawkes processes are used to model time--continuous point processes with history dependence. Here we propose an extended model where the self--effects are of both excitatory and inhibitory type and follow a Gaussian Process. Whereas previous work either relies on a less flexible parameterization of the model, or requires a large amount of data, our formulation allows for both a flexible model and learning when data are scarce. We continue the line of work of Bayesian inference for Hawkes processes, and our approach dispenses with the necessity of estimating a branching structure for the posterior, as we perform inference on an aggregated sum of Gaussian Processes. Efficient approximate Bayesian inference is achieved via data augmentation, and we describe a mean--field variational inference approach to learn the model parameters. To demonstrate the flexibility of the model we apply our methodology on data from three different domains and compare it to previously reported results.

Exact solution to the random sequential dynamics of a message passing algorithm

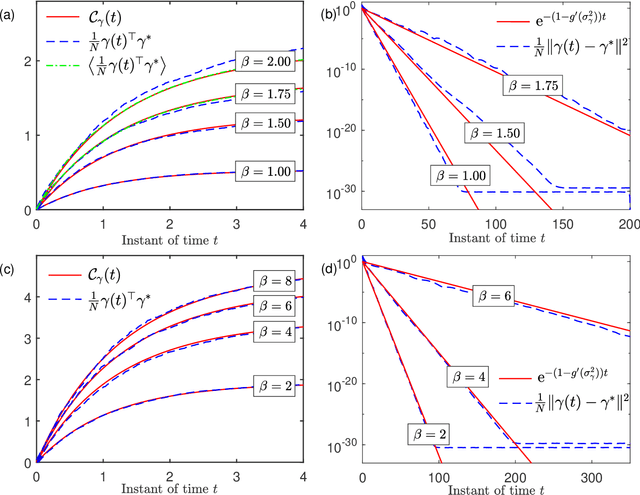
We analyze the random sequential dynamics of a message passing algorithm for Ising models with random interactions in the large system limit. We derive exact results for the two-time correlation functions and the speed of convergence. The {\em de Almedia-Thouless} stability criterion of the static problem is found to be necessary and sufficient for the global convergence of the random sequential dynamics.

A Dynamical Mean-Field Theory for Learning in Restricted Boltzmann Machines

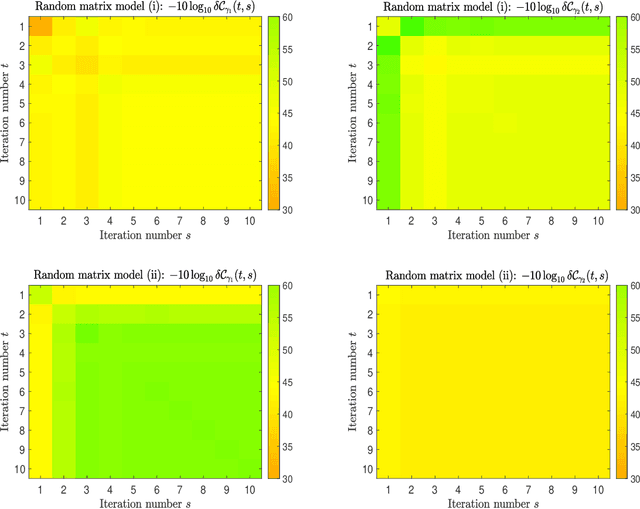
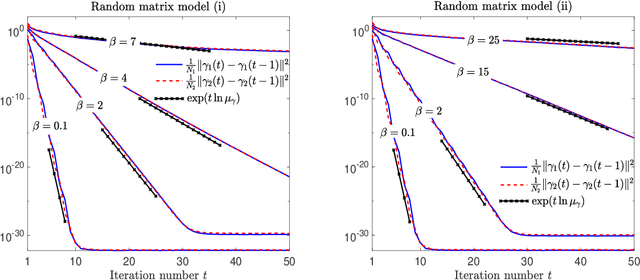
We define a message-passing algorithm for computing magnetizations in Restricted Boltzmann machines, which are Ising models on bipartite graphs introduced as neural network models for probability distributions over spin configurations. To model nontrivial statistical dependencies between the spins' couplings, we assume that the rectangular coupling matrix is drawn from an arbitrary bi-rotation invariant random matrix ensemble. Using the dynamical functional method of statistical mechanics we exactly analyze the dynamics of the algorithm in the large system limit. We prove the global convergence of the algorithm under a stability criterion and compute asymptotic convergence rates showing excellent agreement with numerical simulations.