A Dynamical Mean-Field Theory for Learning in Restricted Boltzmann Machines
Paper and Code
May 04, 2020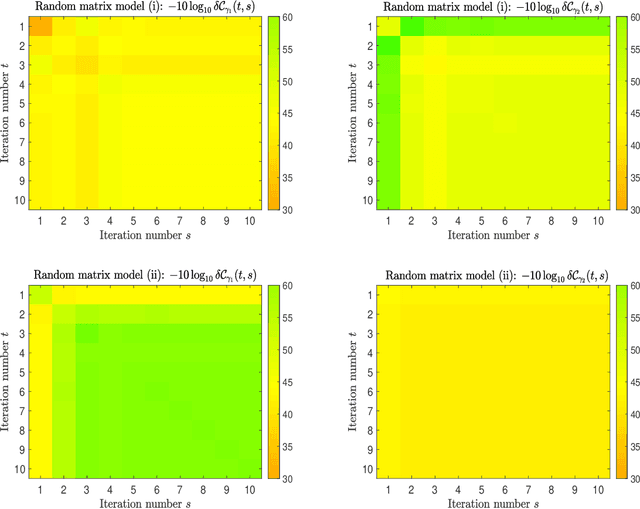
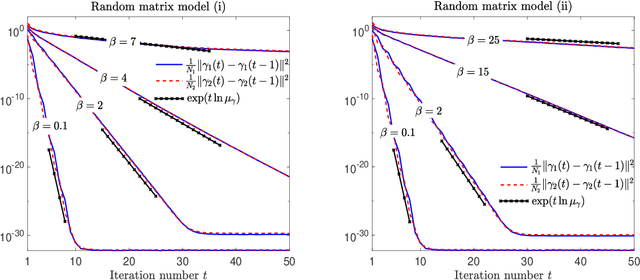
We define a message-passing algorithm for computing magnetizations in Restricted Boltzmann machines, which are Ising models on bipartite graphs introduced as neural network models for probability distributions over spin configurations. To model nontrivial statistical dependencies between the spins' couplings, we assume that the rectangular coupling matrix is drawn from an arbitrary bi-rotation invariant random matrix ensemble. Using the dynamical functional method of statistical mechanics we exactly analyze the dynamics of the algorithm in the large system limit. We prove the global convergence of the algorithm under a stability criterion and compute asymptotic convergence rates showing excellent agreement with numerical simulations.
* 29 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge