A Convergence Analysis of Approximate Message Passing with Non-Separable Functions and Applications to Multi-Class Classification

Motivated by the recent application of approximate message passing (AMP) to the analysis of convex optimizations in multi-class classifications [Loureiro, et. al., 2021], we present a convergence analysis of AMP dynamics with non-separable multivariate nonlinearities. As an application, we present a complete (and independent) analysis of the motivated convex optimization problem.

Analysis of Random Sequential Message Passing Algorithms for Approximate Inference

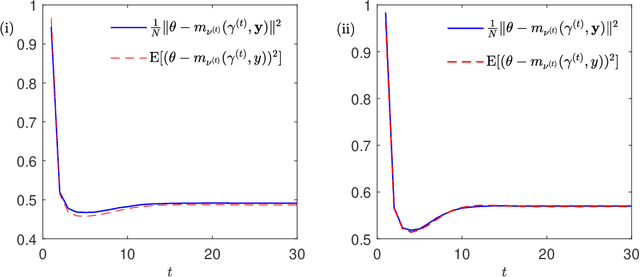
We analyze the dynamics of a random sequential message passing algorithm for approximate inference with large Gaussian latent variable models in a student-teacher scenario. To model nontrivial dependencies between the latent variables, we assume random covariance matrices drawn from rotation invariant ensembles. Moreover, we consider a model mismatching setting, where the teacher model and the one used by the student may be different. By means of dynamical functional approach, we obtain exact dynamical mean-field equations characterizing the dynamics of the inference algorithm. We also derive a range of model parameters for which the sequential algorithm does not converge. The boundary of this parameter range coincides with the de Almeida Thouless (AT) stability condition of the replica symmetric ansatz for the static probabilistic model.

Exact solution to the random sequential dynamics of a message passing algorithm

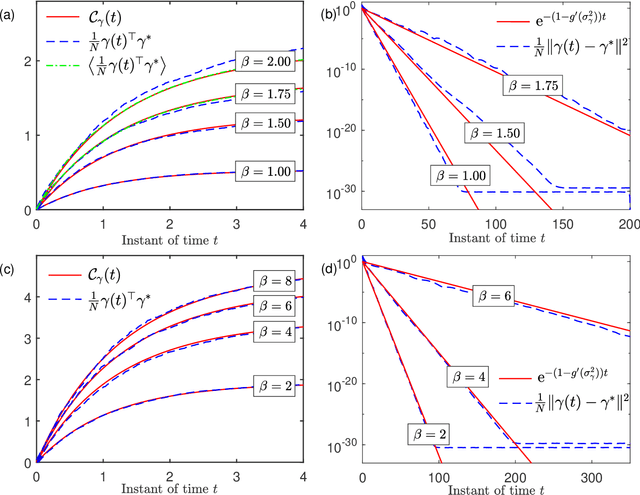
We analyze the random sequential dynamics of a message passing algorithm for Ising models with random interactions in the large system limit. We derive exact results for the two-time correlation functions and the speed of convergence. The {\em de Almedia-Thouless} stability criterion of the static problem is found to be necessary and sufficient for the global convergence of the random sequential dynamics.

A Dynamical Mean-Field Theory for Learning in Restricted Boltzmann Machines

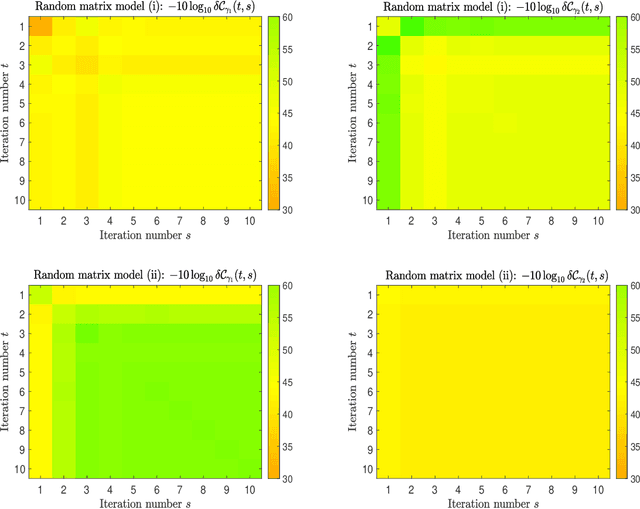
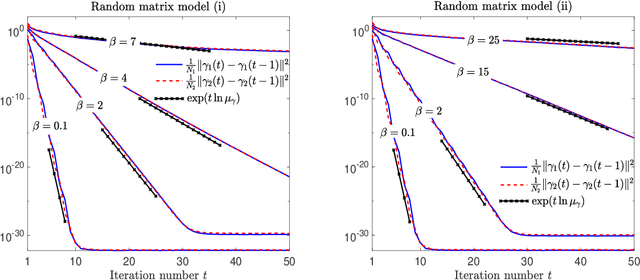
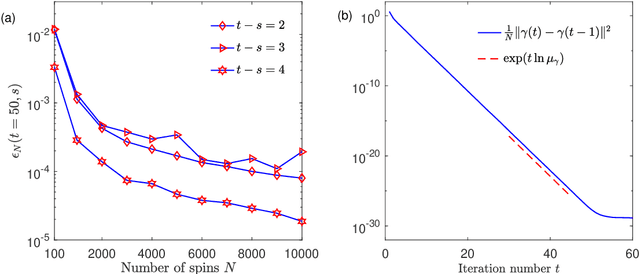
We define a message-passing algorithm for computing magnetizations in Restricted Boltzmann machines, which are Ising models on bipartite graphs introduced as neural network models for probability distributions over spin configurations. To model nontrivial statistical dependencies between the spins' couplings, we assume that the rectangular coupling matrix is drawn from an arbitrary bi-rotation invariant random matrix ensemble. Using the dynamical functional method of statistical mechanics we exactly analyze the dynamics of the algorithm in the large system limit. We prove the global convergence of the algorithm under a stability criterion and compute asymptotic convergence rates showing excellent agreement with numerical simulations.

Understanding the dynamics of message passing algorithms: a free probability heuristics

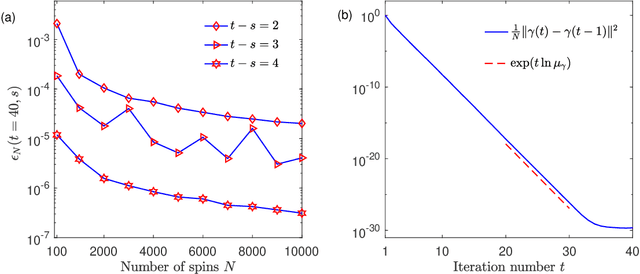
We use freeness assumptions of random matrix theory to analyze the dynamical behavior of inference algorithms for probabilistic models with dense coupling matrices in the limit of large systems. For a toy Ising model, we are able to recover previous results such as the property of vanishing effective memories and the analytical convergence rate of the algorithm.

Analysis of Bayesian Inference Algorithms by the Dynamical Functional Approach

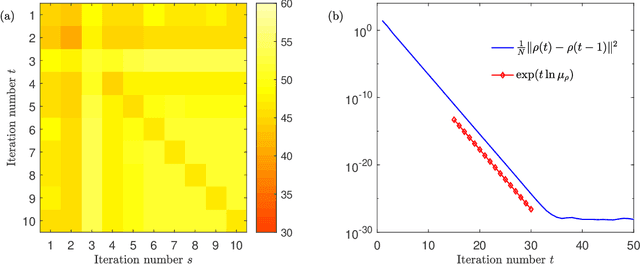
We analyze the dynamics of an algorithm for approximate inference with large Gaussian latent variable models in a student-teacher scenario. To model nontrivial dependencies between the latent variables, we assume random covariance matrices drawn from rotation invariant ensembles. For the case of perfect data-model matching, the knowledge of static order parameters derived from the replica method allows us to obtain efficient algorithmic updates in terms of matrix-vector multiplications with a fixed matrix. Using the dynamical functional approach, we obtain an exact effective stochastic process in the thermodynamic limit for a single node. From this, we obtain closed-form expressions for the rate of the convergence. Analytical results are excellent agreement with simulations of single instances of large models.

Convergent Dynamics for Solving the TAP Equations of Ising Models with Arbitrary Rotation Invariant Coupling Matrices

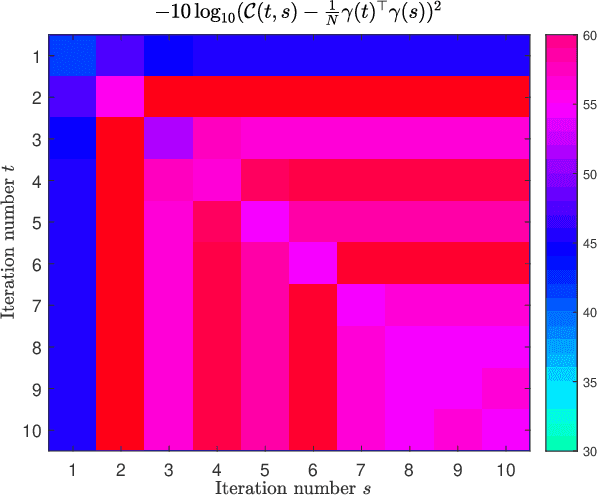
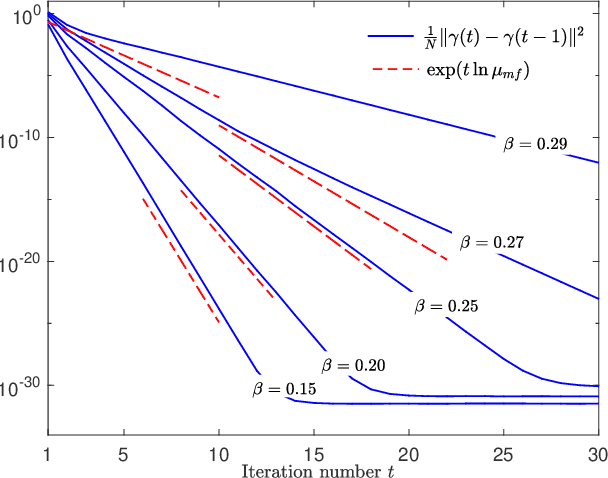
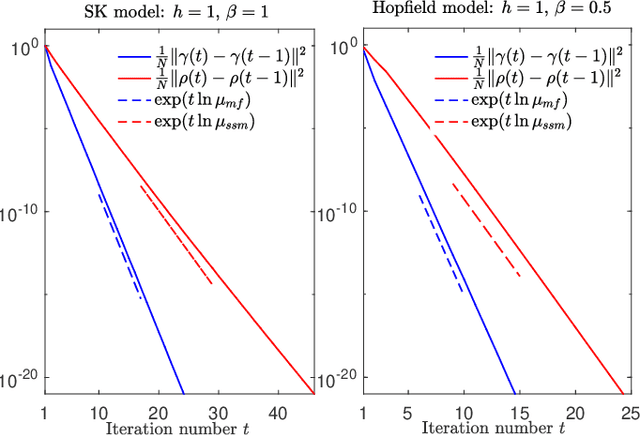
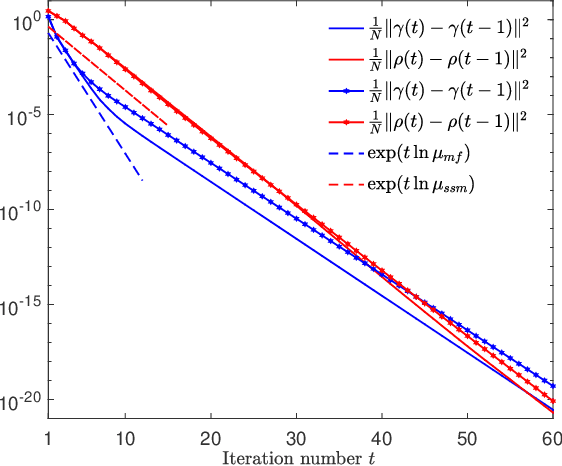
We propose an iterative algorithm for solving the Thouless-Anderson-Palmer (TAP) equations of Ising models with arbitrary rotation invariant (random) coupling matrices. In the large-system limit, as the number of iterations tends to infinity we prove by means of the dynamical functional method that the proposed algorithm converges when the so-called de Almeida Thouless (AT) criterion is fulfilled. Moreover, we obtain an analytical expression for the rate of the convergence.

Expectation Propagation for Approximate Inference: Free Probability Framework

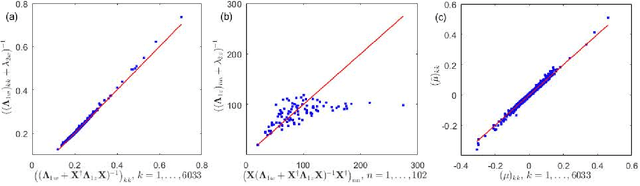
We study asymptotic properties of expectation propagation (EP) -- a method for approximate inference originally developed in the field of machine learning. Applied to generalized linear models, EP iteratively computes a multivariate Gaussian approximation to the exact posterior distribution. The computational complexity of the repeated update of covariance matrices severely limits the application of EP to large problem sizes. In this study, we present a rigorous analysis by means of free probability theory that allows us to overcome this computational bottleneck if specific data matrices in the problem fulfill certain properties of asymptotic freeness. We demonstrate the relevance of our approach on the gene selection problem of a microarray dataset.

Self-Averaging Expectation Propagation

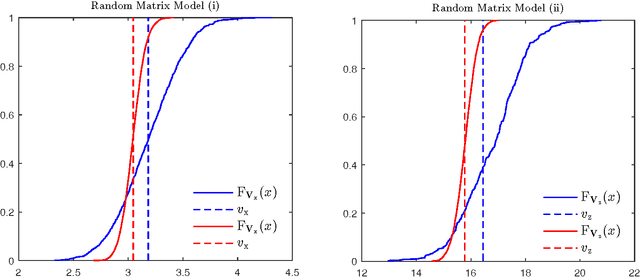
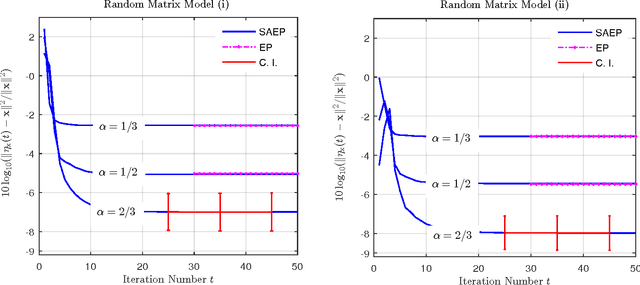
We investigate the problem of approximate Bayesian inference for a general class of observation models by means of the expectation propagation (EP) framework for large systems under some statistical assumptions. Our approach tries to overcome the numerical bottleneck of EP caused by the inversion of large matrices. Assuming that the measurement matrices are realizations of specific types of ensembles we use the concept of freeness from random matrix theory to show that the EP cavity variances exhibit an asymptotic self-averaging property. They can be pre-computed using specific generating functions, i.e. the R- and/or S-transforms in free probability, which do not require matrix inversions. Our approach extends the framework of (generalized) approximate message passing -- assumes zero-mean iid entries of the measurement matrix -- to a general class of random matrix ensembles. The generalization is via a simple formulation of the R- and/or S-transforms of the limiting eigenvalue distribution of the Gramian of the measurement matrix. We demonstrate the performance of our approach on a signal recovery problem of nonlinear compressed sensing and compare it with that of EP.