Analysis of Bayesian Inference Algorithms by the Dynamical Functional Approach
Paper and Code
Jan 14, 2020
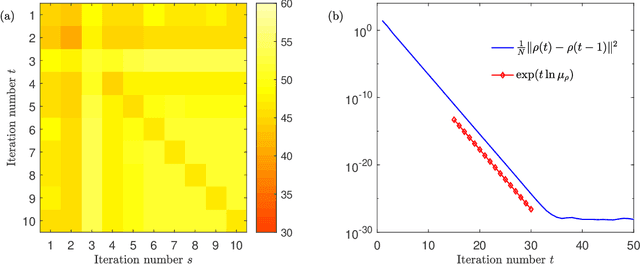
We analyze the dynamics of an algorithm for approximate inference with large Gaussian latent variable models in a student-teacher scenario. To model nontrivial dependencies between the latent variables, we assume random covariance matrices drawn from rotation invariant ensembles. For the case of perfect data-model matching, the knowledge of static order parameters derived from the replica method allows us to obtain efficient algorithmic updates in terms of matrix-vector multiplications with a fixed matrix. Using the dynamical functional approach, we obtain an exact effective stochastic process in the thermodynamic limit for a single node. From this, we obtain closed-form expressions for the rate of the convergence. Analytical results are excellent agreement with simulations of single instances of large models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge