Self-Averaging Expectation Propagation
Paper and Code
Aug 23, 2016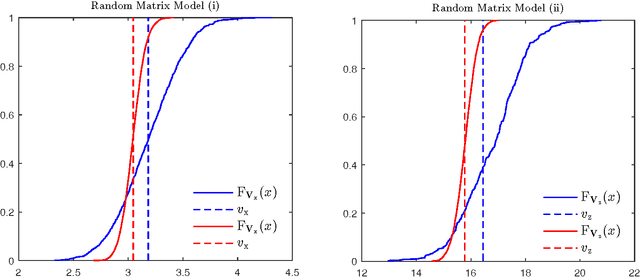
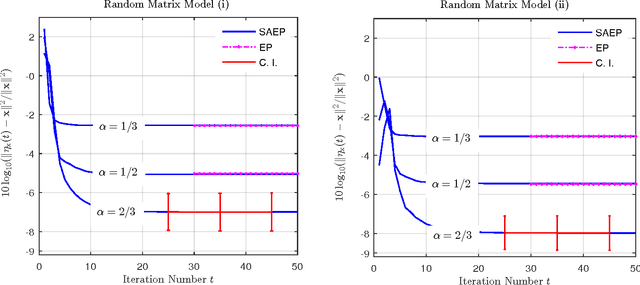
We investigate the problem of approximate Bayesian inference for a general class of observation models by means of the expectation propagation (EP) framework for large systems under some statistical assumptions. Our approach tries to overcome the numerical bottleneck of EP caused by the inversion of large matrices. Assuming that the measurement matrices are realizations of specific types of ensembles we use the concept of freeness from random matrix theory to show that the EP cavity variances exhibit an asymptotic self-averaging property. They can be pre-computed using specific generating functions, i.e. the R- and/or S-transforms in free probability, which do not require matrix inversions. Our approach extends the framework of (generalized) approximate message passing -- assumes zero-mean iid entries of the measurement matrix -- to a general class of random matrix ensembles. The generalization is via a simple formulation of the R- and/or S-transforms of the limiting eigenvalue distribution of the Gramian of the measurement matrix. We demonstrate the performance of our approach on a signal recovery problem of nonlinear compressed sensing and compare it with that of EP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge