Super-Resolution Estimation of UWB Channels including the Diffuse Component -- An SBL-Inspired Approach

In this paper, we present an iterative algorithm that detects and estimates the specular components and estimates the diffuse component of single-input-multiple-output (SIMO) ultra-wide-band (UWB) multipath channels. Specifically, the algorithm super-resolves the specular components in the delay-angle-of-arrival domain and estimates the parameters of a parametric model of the delay-angle power spectrum characterizing the diffuse component. Channel noise is also estimated. In essence, the algorithm solves the problem of estimating spectral lines (the specular components) in colored noise (generated by the diffuse component and channel noise). Its design is inspired by the sparse Bayesian learning (SBL) framework. As a result the iteration process contains a threshold condition that determines whether a candidate specular component shall be retained or pruned. By relying to results from extreme-value analysis the threshold of this condition is suitably adapted to ensure a prescribed probability of detecting spurious specular components. Studies using synthetic and real channel measurement data demonstrate the virtues of the algorithm: it is able to still detect and accurately estimate specular components, even when their separation in delay and angle is down to half the Rayleigh resolution limit (RRL) of the equipment; it is robust in the sense that it tends to return no more specular components than the actual ones. Finally, the algorithm is shown to outperform a state-of-the-art super-resolution channel estimator.

Self-Averaging Expectation Propagation

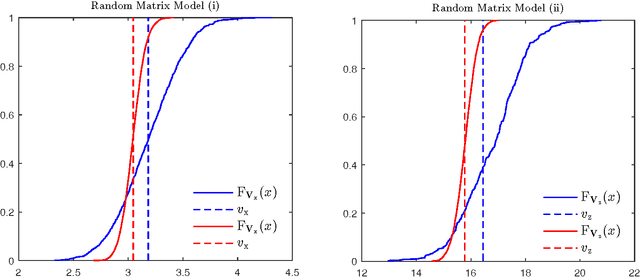
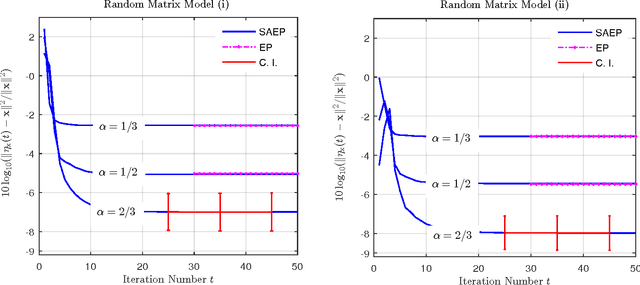
We investigate the problem of approximate Bayesian inference for a general class of observation models by means of the expectation propagation (EP) framework for large systems under some statistical assumptions. Our approach tries to overcome the numerical bottleneck of EP caused by the inversion of large matrices. Assuming that the measurement matrices are realizations of specific types of ensembles we use the concept of freeness from random matrix theory to show that the EP cavity variances exhibit an asymptotic self-averaging property. They can be pre-computed using specific generating functions, i.e. the R- and/or S-transforms in free probability, which do not require matrix inversions. Our approach extends the framework of (generalized) approximate message passing -- assumes zero-mean iid entries of the measurement matrix -- to a general class of random matrix ensembles. The generalization is via a simple formulation of the R- and/or S-transforms of the limiting eigenvalue distribution of the Gramian of the measurement matrix. We demonstrate the performance of our approach on a signal recovery problem of nonlinear compressed sensing and compare it with that of EP.

Receiver Architectures for MIMO-OFDM Based on a Combined VMP-SP Algorithm

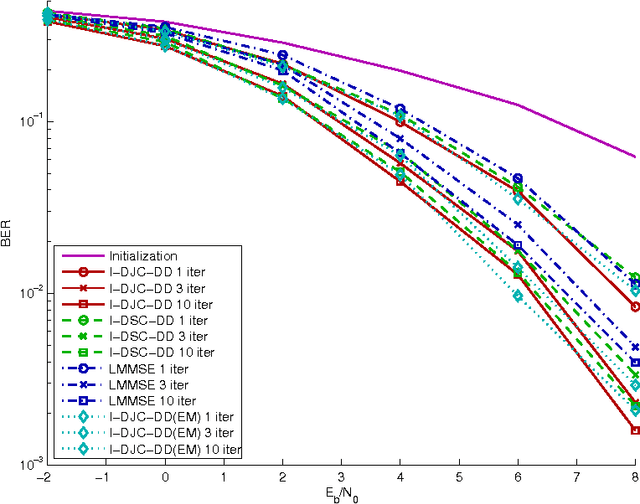
Iterative information processing, either based on heuristics or analytical frameworks, has been shown to be a very powerful tool for the design of efficient, yet feasible, wireless receiver architectures. Within this context, algorithms performing message-passing on a probabilistic graph, such as the sum-product (SP) and variational message passing (VMP) algorithms, have become increasingly popular. In this contribution, we apply a combined VMP-SP message-passing technique to the design of receivers for MIMO-ODFM systems. The message-passing equations of the combined scheme can be obtained from the equations of the stationary points of a constrained region-based free energy approximation. When applied to a MIMO-OFDM probabilistic model, we obtain a generic receiver architecture performing iterative channel weight and noise precision estimation, equalization and data decoding. We show that this generic scheme can be particularized to a variety of different receiver structures, ranging from high-performance iterative structures to low complexity receivers. This allows for a flexible design of the signal processing specially tailored for the requirements of each specific application. The numerical assessment of our solutions, based on Monte Carlo simulations, corroborates the high performance of the proposed algorithms and their superiority to heuristic approaches.