Generating Rectifiable Measures through Neural Networks

We derive universal approximation results for the class of (countably) $m$-rectifiable measures. Specifically, we prove that $m$-rectifiable measures can be approximated as push-forwards of the one-dimensional Lebesgue measure on $[0,1]$ using ReLU neural networks with arbitrarily small approximation error in terms of Wasserstein distance. What is more, the weights in the networks under consideration are quantized and bounded and the number of ReLU neural networks required to achieve an approximation error of $\varepsilon$ is no larger than $2^{b(\varepsilon)}$ with $b(\varepsilon)=\mathcal{O}(\varepsilon^{-m}\log^2(\varepsilon))$. This result improves Lemma IX.4 in Perekrestenko et al. as it shows that the rate at which $b(\varepsilon)$ tends to infinity as $\varepsilon$ tends to zero equals the rectifiability parameter $m$, which can be much smaller than the ambient dimension. We extend this result to countably $m$-rectifiable measures and show that this rate still equals the rectifiability parameter $m$ provided that, among other technical assumptions, the measure decays exponentially on the individual components of the countably $m$-rectifiable support set.

Message-Passing Algorithms for Channel Estimation and Decoding Using Approximate Inference

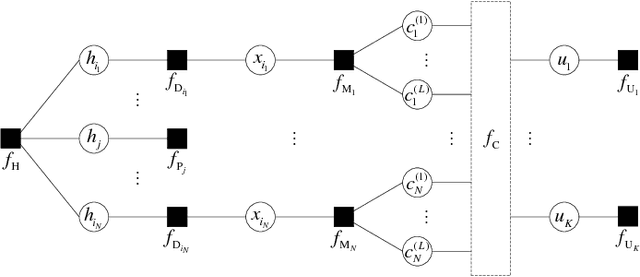
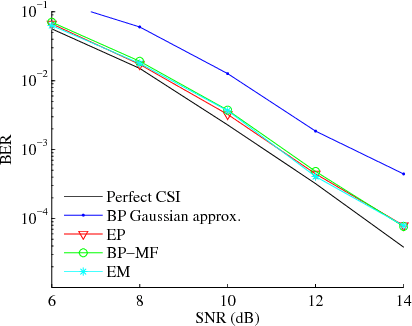
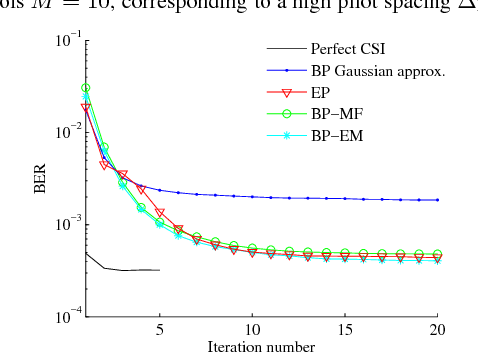
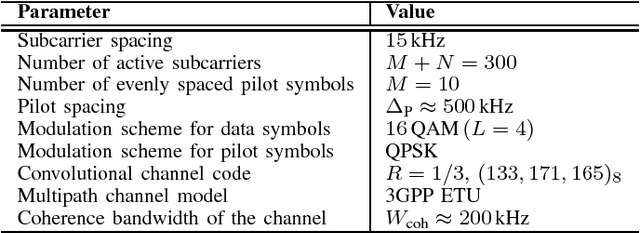
We design iterative receiver schemes for a generic wireless communication system by treating channel estimation and information decoding as an inference problem in graphical models. We introduce a recently proposed inference framework that combines belief propagation (BP) and the mean field (MF) approximation and includes these algorithms as special cases. We also show that the expectation propagation and expectation maximization algorithms can be embedded in the BP-MF framework with slight modifications. By applying the considered inference algorithms to our probabilistic model, we derive four different message-passing receiver schemes. Our numerical evaluation demonstrates that the receiver based on the BP-MF framework and its variant based on BP-EM yield the best compromise between performance, computational complexity and numerical stability among all candidate algorithms.

Merging Belief Propagation and the Mean Field Approximation: A Free Energy Approach

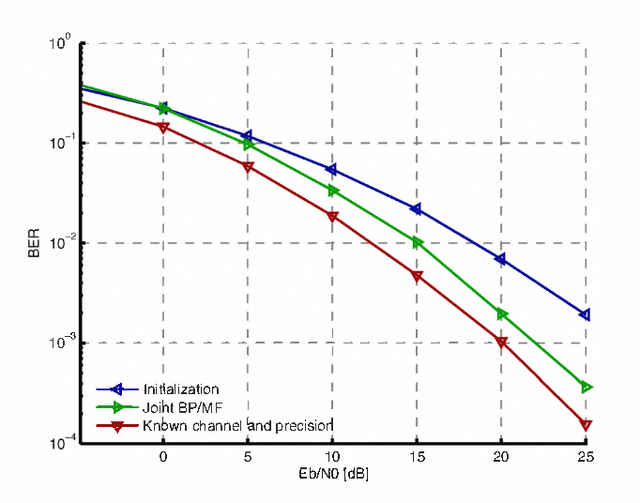
We present a joint message passing approach that combines belief propagation and the mean field approximation. Our analysis is based on the region-based free energy approximation method proposed by Yedidia et al. We show that the message passing fixed-point equations obtained with this combination correspond to stationary points of a constrained region-based free energy approximation. Moreover, we present a convergent implementation of these message passing fixedpoint equations provided that the underlying factor graph fulfills certain technical conditions. In addition, we show how to include hard constraints in the part of the factor graph corresponding to belief propagation. Finally, we demonstrate an application of our method to iterative channel estimation and decoding in an orthogonal frequency division multiplexing (OFDM) system.

Receiver Architectures for MIMO-OFDM Based on a Combined VMP-SP Algorithm

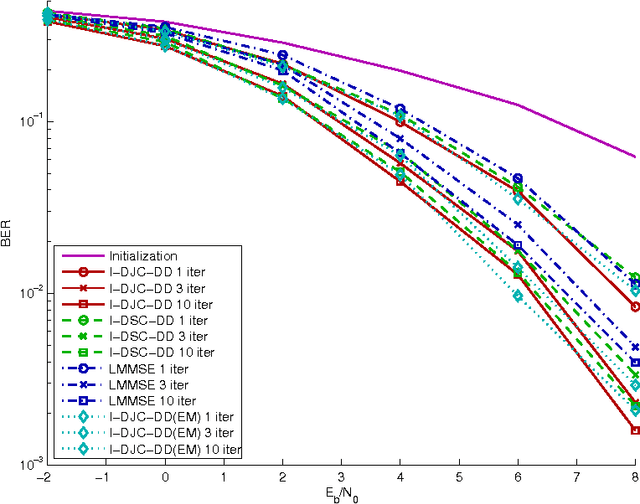
Iterative information processing, either based on heuristics or analytical frameworks, has been shown to be a very powerful tool for the design of efficient, yet feasible, wireless receiver architectures. Within this context, algorithms performing message-passing on a probabilistic graph, such as the sum-product (SP) and variational message passing (VMP) algorithms, have become increasingly popular. In this contribution, we apply a combined VMP-SP message-passing technique to the design of receivers for MIMO-ODFM systems. The message-passing equations of the combined scheme can be obtained from the equations of the stationary points of a constrained region-based free energy approximation. When applied to a MIMO-OFDM probabilistic model, we obtain a generic receiver architecture performing iterative channel weight and noise precision estimation, equalization and data decoding. We show that this generic scheme can be particularized to a variety of different receiver structures, ranging from high-performance iterative structures to low complexity receivers. This allows for a flexible design of the signal processing specially tailored for the requirements of each specific application. The numerical assessment of our solutions, based on Monte Carlo simulations, corroborates the high performance of the proposed algorithms and their superiority to heuristic approaches.