Variational Bayesian Inference of Line Spectra

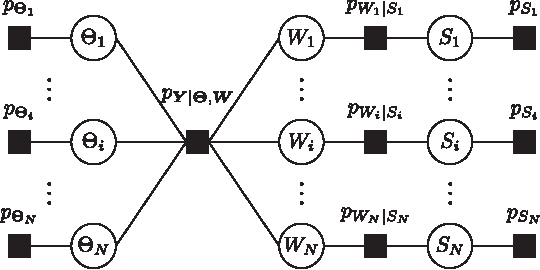
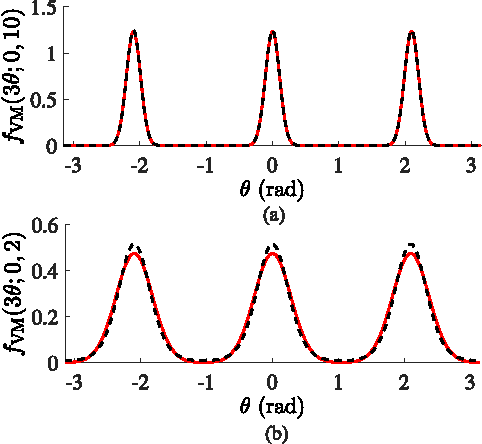
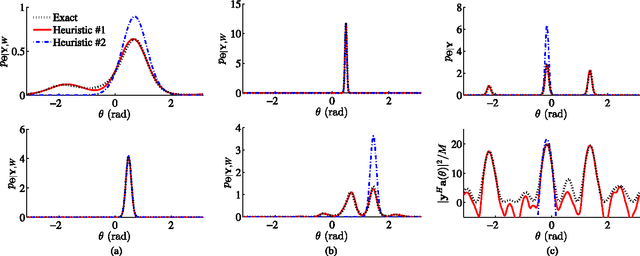
In this paper, we address the fundamental problem of line spectral estimation in a Bayesian framework. We target model order and parameter estimation via variational inference in a probabilistic model in which the frequencies are continuous-valued, i.e., not restricted to a grid; and the coefficients are governed by a Bernoulli-Gaussian prior model turning model order selection into binary sequence detection. Unlike earlier works which retain only point estimates of the frequencies, we undertake a more complete Bayesian treatment by estimating the posterior probability density functions (pdfs) of the frequencies and computing expectations over them. Thus, we additionally capture and operate with the uncertainty of the frequency estimates. Aiming to maximize the model evidence, variational optimization provides analytic approximations of the posterior pdfs and also gives estimates of the additional parameters. We propose an accurate representation of the pdfs of the frequencies by mixtures of von Mises pdfs, which yields closed-form expectations. We define the algorithm VALSE in which the estimates of the pdfs and parameters are iteratively updated. VALSE is a gridless, convergent method, does not require parameter tuning, can easily include prior knowledge about the frequencies and provides approximate posterior pdfs based on which the uncertainty in line spectral estimation can be quantified. Simulation results show that accounting for the uncertainty of frequency estimates, rather than computing just point estimates, significantly improves the performance. The performance of VALSE is superior to that of state-of-the-art methods and closely approaches the Cram\'er-Rao bound computed for the true model order.

Sparse Estimation using Bayesian Hierarchical Prior Modeling for Real and Complex Linear Models

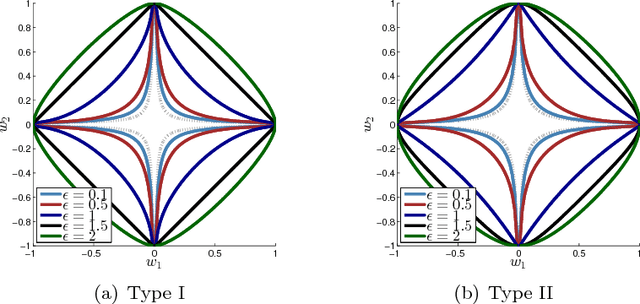
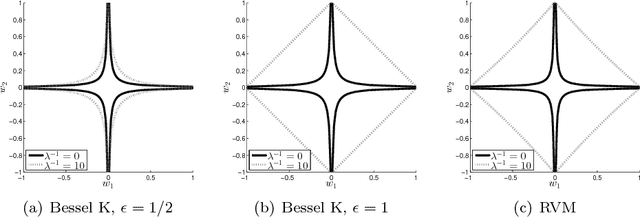
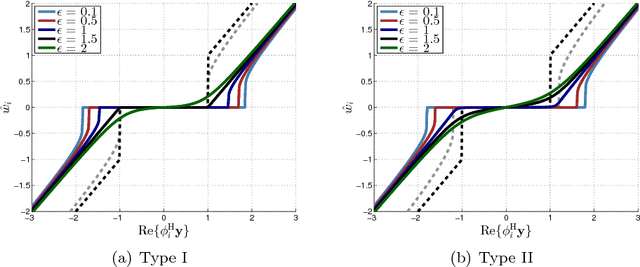
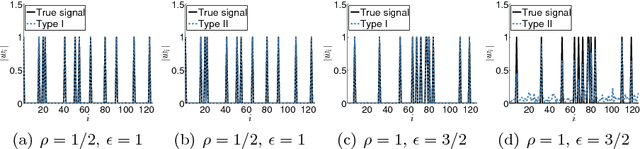
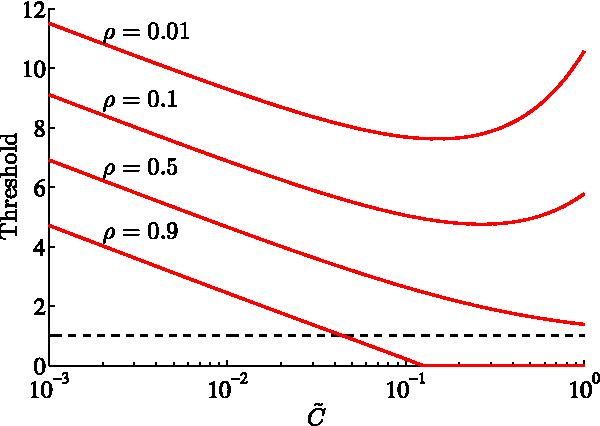
In sparse Bayesian learning (SBL), Gaussian scale mixtures (GSMs) have been used to model sparsity-inducing priors that realize a class of concave penalty functions for the regression task in real-valued signal models. Motivated by the relative scarcity of formal tools for SBL in complex-valued models, this paper proposes a GSM model - the Bessel K model - that induces concave penalty functions for the estimation of complex sparse signals. The properties of the Bessel K model are analyzed when it is applied to Type I and Type II estimation. This analysis reveals that, by tuning the parameters of the mixing pdf different penalty functions are invoked depending on the estimation type used, the value of the noise variance, and whether real or complex signals are estimated. Using the Bessel K model, we derive a sparse estimator based on a modification of the expectation-maximization algorithm formulated for Type II estimation. The estimator includes as a special instance the algorithms proposed by Tipping and Faul [1] and by Babacan et al. [2]. Numerical results show the superiority of the proposed estimator over these state-of-the-art estimators in terms of convergence speed, sparseness, reconstruction error, and robustness in low and medium signal-to-noise ratio regimes.

Message-Passing Algorithms for Channel Estimation and Decoding Using Approximate Inference

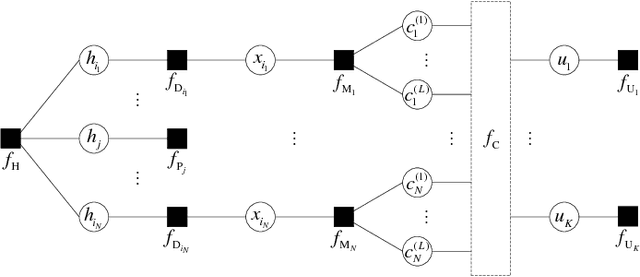
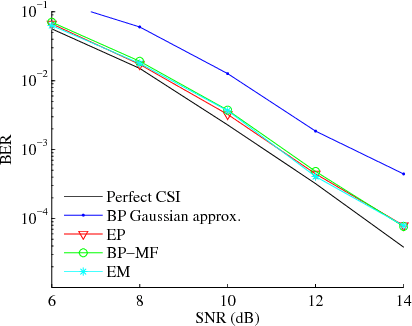
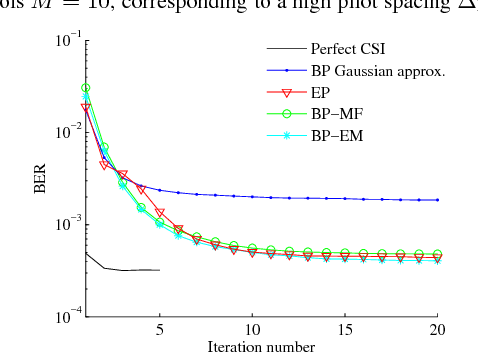
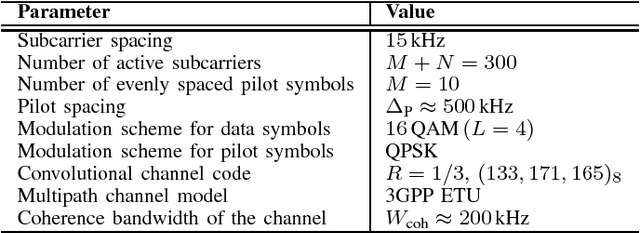
We design iterative receiver schemes for a generic wireless communication system by treating channel estimation and information decoding as an inference problem in graphical models. We introduce a recently proposed inference framework that combines belief propagation (BP) and the mean field (MF) approximation and includes these algorithms as special cases. We also show that the expectation propagation and expectation maximization algorithms can be embedded in the BP-MF framework with slight modifications. By applying the considered inference algorithms to our probabilistic model, we derive four different message-passing receiver schemes. Our numerical evaluation demonstrates that the receiver based on the BP-MF framework and its variant based on BP-EM yield the best compromise between performance, computational complexity and numerical stability among all candidate algorithms.

Distributed Iterative Processing for Interference Channels with Receiver Cooperation

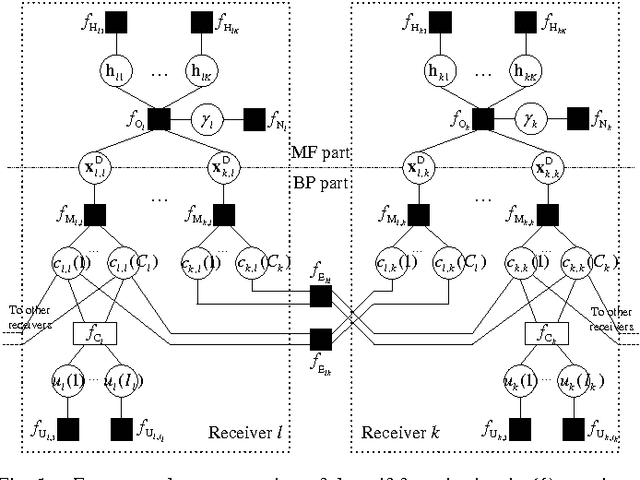
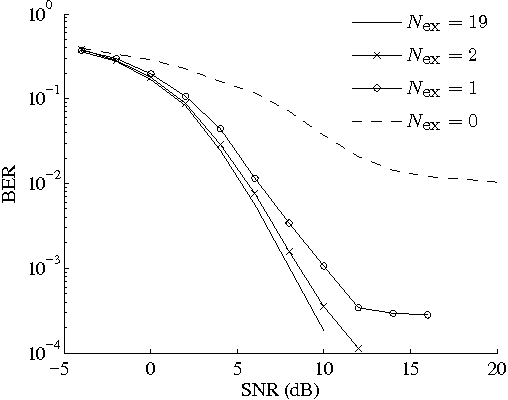
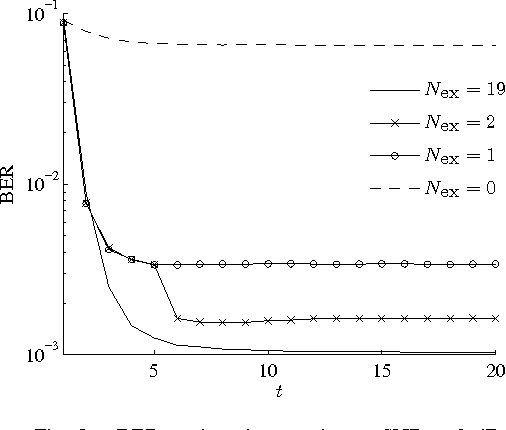
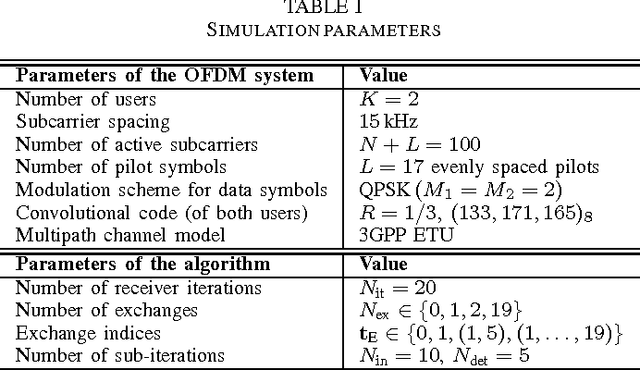
We propose a framework for the derivation and evaluation of distributed iterative algorithms for receiver cooperation in interference-limited wireless systems. Our approach views the processing within and collaboration between receivers as the solution to an inference problem in the probabilistic model of the whole system. The probabilistic model is formulated to explicitly incorporate the receivers' ability to share information of a predefined type. We employ a recently proposed unified message-passing tool to infer the variables of interest in the factor graph representation of the probabilistic model. The exchange of information between receivers arises in the form of passing messages along some specific edges of the factor graph; the rate of updating and passing these messages determines the communication overhead associated with cooperation. Simulation results illustrate the high performance of the proposed algorithm even with a low number of message exchanges between receivers.

Application of Bayesian Hierarchical Prior Modeling to Sparse Channel Estimation

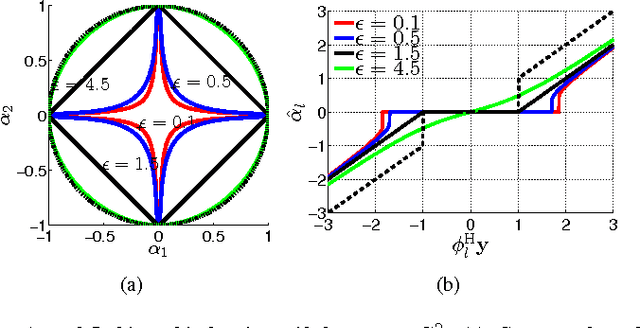
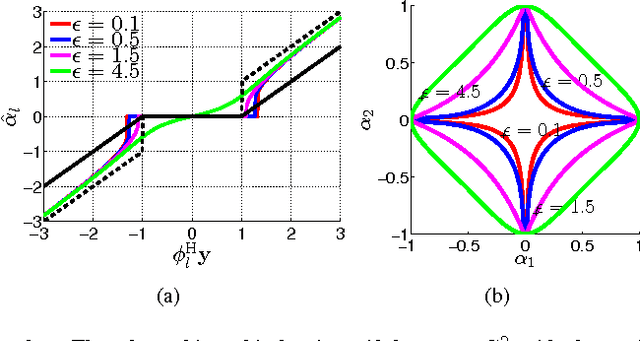
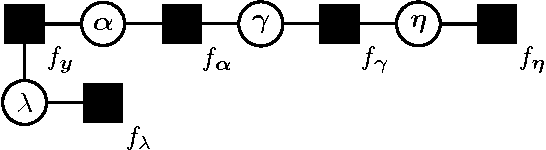
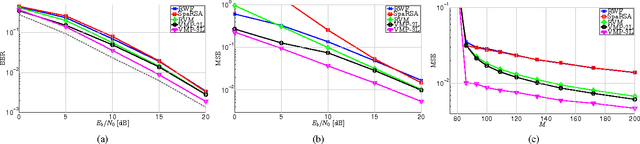
Existing methods for sparse channel estimation typically provide an estimate computed as the solution maximizing an objective function defined as the sum of the log-likelihood function and a penalization term proportional to the l1-norm of the parameter of interest. However, other penalization terms have proven to have strong sparsity-inducing properties. In this work, we design pilot-assisted channel estimators for OFDM wireless receivers within the framework of sparse Bayesian learning by defining hierarchical Bayesian prior models that lead to sparsity-inducing penalization terms. The estimators result as an application of the variational message-passing algorithm on the factor graph representing the signal model extended with the hierarchical prior models. Numerical results demonstrate the superior performance of our channel estimators as compared to traditional and state-of-the-art sparse methods.