Sparse Estimation using Bayesian Hierarchical Prior Modeling for Real and Complex Linear Models

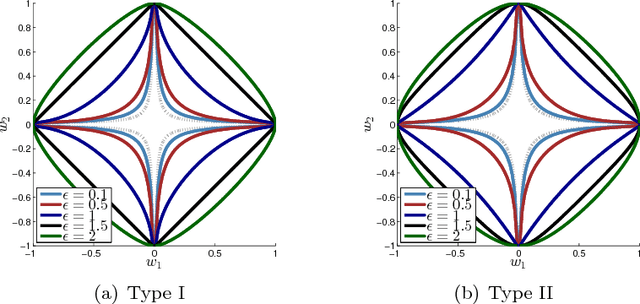
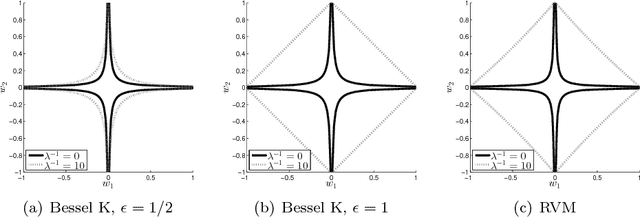
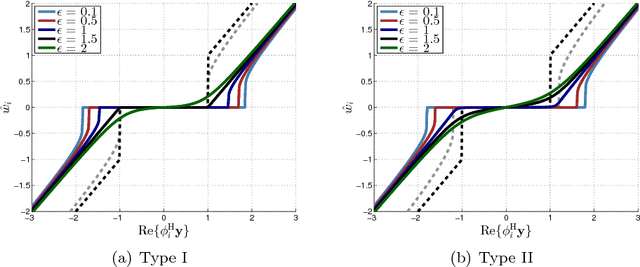
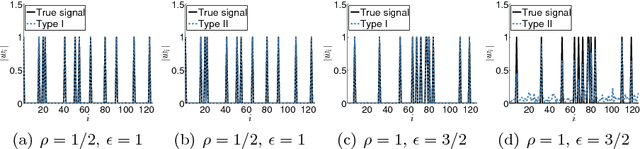
In sparse Bayesian learning (SBL), Gaussian scale mixtures (GSMs) have been used to model sparsity-inducing priors that realize a class of concave penalty functions for the regression task in real-valued signal models. Motivated by the relative scarcity of formal tools for SBL in complex-valued models, this paper proposes a GSM model - the Bessel K model - that induces concave penalty functions for the estimation of complex sparse signals. The properties of the Bessel K model are analyzed when it is applied to Type I and Type II estimation. This analysis reveals that, by tuning the parameters of the mixing pdf different penalty functions are invoked depending on the estimation type used, the value of the noise variance, and whether real or complex signals are estimated. Using the Bessel K model, we derive a sparse estimator based on a modification of the expectation-maximization algorithm formulated for Type II estimation. The estimator includes as a special instance the algorithms proposed by Tipping and Faul [1] and by Babacan et al. [2]. Numerical results show the superiority of the proposed estimator over these state-of-the-art estimators in terms of convergence speed, sparseness, reconstruction error, and robustness in low and medium signal-to-noise ratio regimes.

A Fast Iterative Bayesian Inference Algorithm for Sparse Channel Estimation

In this paper, we present a Bayesian channel estimation algorithm for multicarrier receivers based on pilot symbol observations. The inherent sparse nature of wireless multipath channels is exploited by modeling the prior distribution of multipath components' gains with a hierarchical representation of the Bessel K probability density function; a highly efficient, fast iterative Bayesian inference method is then applied to the proposed model. The resulting estimator outperforms other state-of-the-art Bayesian and non-Bayesian estimators, either by yielding lower mean squared estimation error or by attaining the same accuracy with improved convergence rate, as shown in our numerical evaluation.

Application of Bayesian Hierarchical Prior Modeling to Sparse Channel Estimation

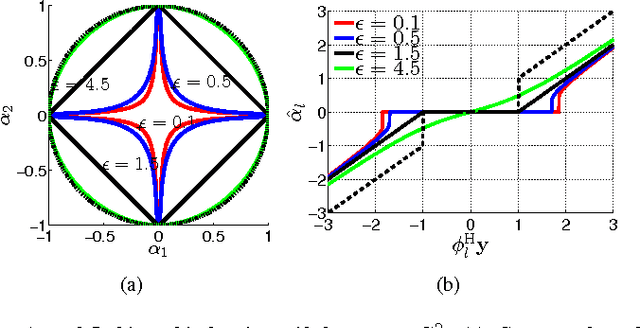
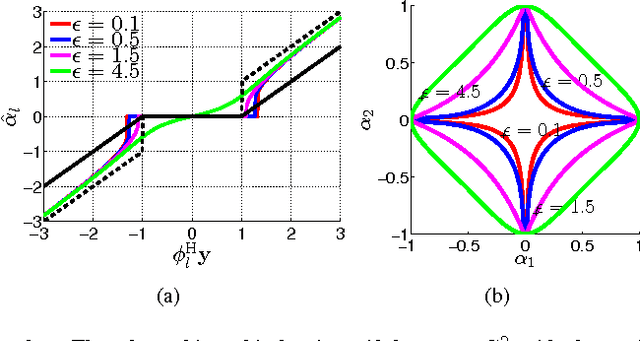
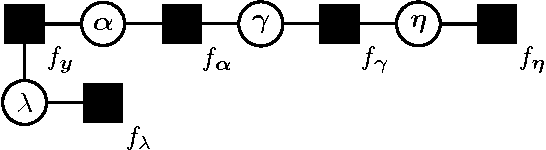
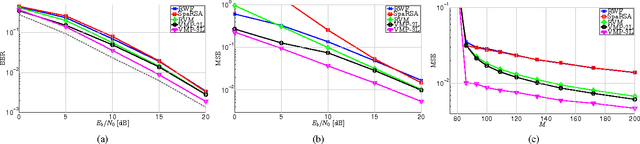
Existing methods for sparse channel estimation typically provide an estimate computed as the solution maximizing an objective function defined as the sum of the log-likelihood function and a penalization term proportional to the l1-norm of the parameter of interest. However, other penalization terms have proven to have strong sparsity-inducing properties. In this work, we design pilot-assisted channel estimators for OFDM wireless receivers within the framework of sparse Bayesian learning by defining hierarchical Bayesian prior models that lead to sparsity-inducing penalization terms. The estimators result as an application of the variational message-passing algorithm on the factor graph representing the signal model extended with the hierarchical prior models. Numerical results demonstrate the superior performance of our channel estimators as compared to traditional and state-of-the-art sparse methods.