Performance Analysis of RIS-Assisted Large-Scale Wireless Networks Using Stochastic Geometry

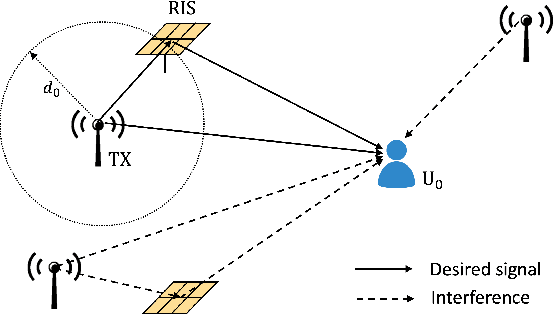
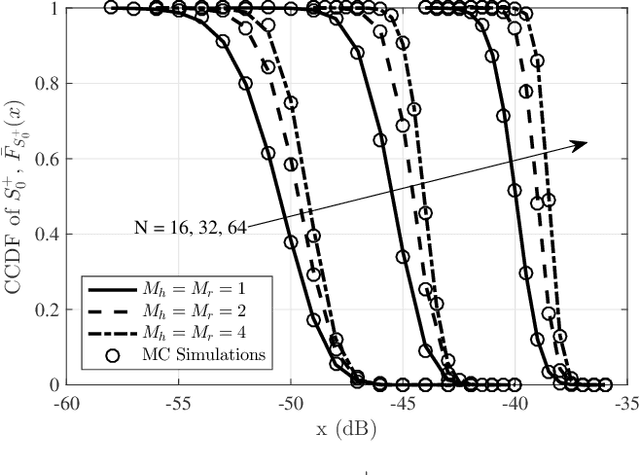
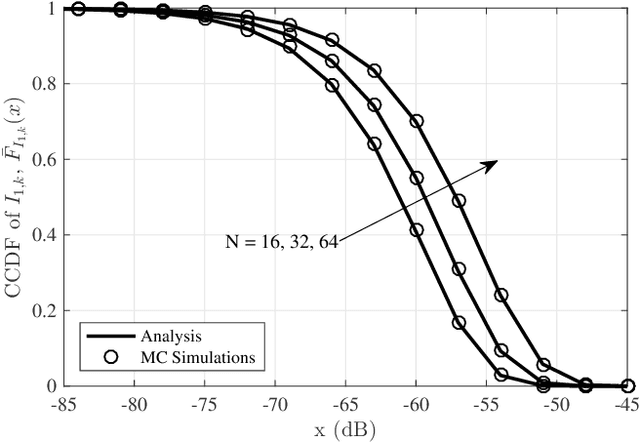
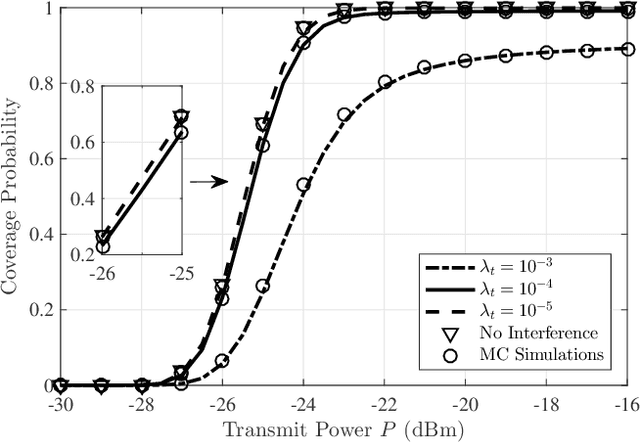
In this paper, we investigate the performance of a reconfigurable intelligent surface (RIS) assisted large-scale network by characterizing the coverage probability and the average achievable rate using stochastic geometry. Considering the spatial correlation between transmitters (TXs) and RISs, their locations are jointly modelled by a Gauss-Poisson process (GPP). Two association strategies, i.e., nearest association and fixed association, are both discussed. For the RIS-aided transmission, the signal power distribution with a direct link is approximated by a gamma random variable using a moment matching method, and the Laplace transform of the aggregate interference power is derived in closed form. Based on these expressions, we analyze the channel hardening effect in the RIS-assisted transmission, the coverage probability, and the average achievable rate of the typical user. We derive the coverage probability expressions for the fixed association strategy and the nearest association strategy in an interference-limited scenario in closed form. Numerical results are provided to validate the analysis and illustrate the effectiveness of RIS-assisted transmission with passive beamforming in improving the system performance. Furthermore, it is also unveiled that the system performance is independent of the density of TXs with the nearest association strategy in the interference-limited scenario.

Performance Analysis of IOS-Assisted NOMA System with Channel Correlation and Phase Errors

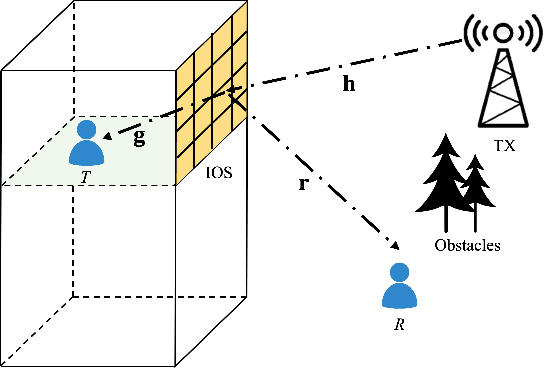
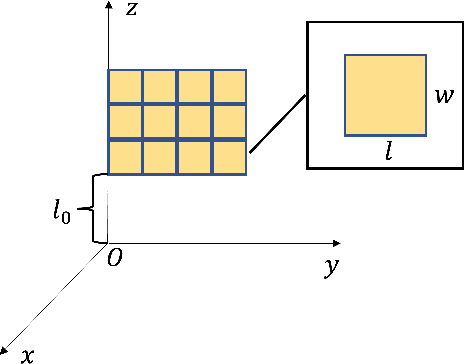
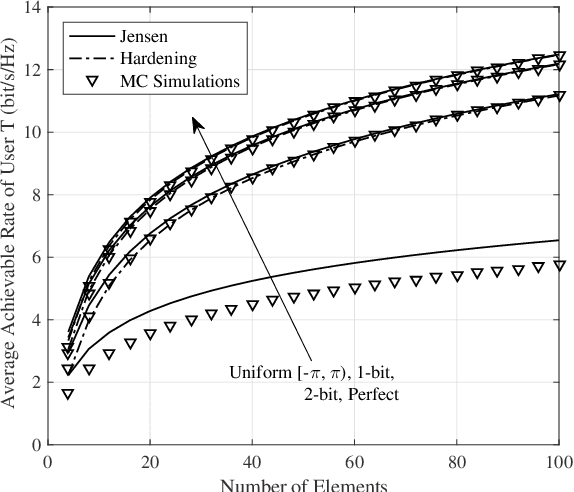
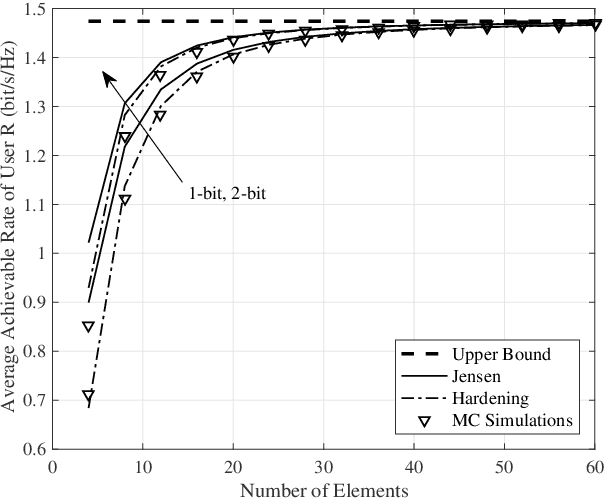
In this paper, we investigate the performance of an intelligent omni-surface (IOS) assisted downlink non-orthogonal multiple access (NOMA) network with phase quantization errors and channel estimation errors, where the channels related to the IOS are spatially correlated. First, upper bounds on the average achievable rates of the two users are derived. Then, channel hardening is shown to occur in the proposed system, based on which we derive approximations of the average achievable rates of the two users. The analytical results illustrate that the proposed upper bound and approximation on the average achievable rate of the strong user are asymptotically equivalent in the number of elements. Furthermore, it is proved that the average achievable rates with correlated and uncorrelated channels are asymptotically equivalent for a large number of elements. Simulation results corroborate the theoretical analysis and show that the channel hardening effect appears even for a few elements. The impact of channel correlation on the system performance in terms of average achievable rates is negligible for a large number of elements.

Model-Based Detector for SSDs in the Presence of Inter-cell Interference

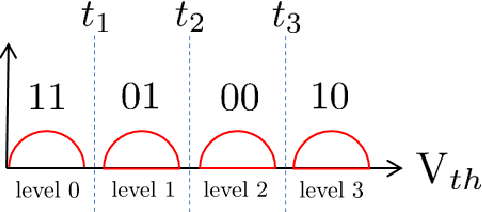
In this paper, we consider the problem of reducing the bit error rate of flash-based solid state drives (SSDs) when cells are subject to inter-cell interference (ICI). By observing that the outputs of adjacent victim cells can be correlated due to common aggressors, we propose a novel channel model to accurately represent the true flash channel. This model, equivalent to a finite-state Markov channel model, allows the use of the sum-product algorithm to calculate more accurate posterior distributions of individual cell inputs given the joint outputs of victim cells. These posteriors can be easily mapped to the log-likelihood ratios that are passed as inputs to the soft LDPC decoder. When the output is available with high precision, our simulation showed that a significant reduction in the bit-error rate can be obtained, reaching $99.99\%$ reduction compared to current methods, when the diagonal coupling is very strong. In the realistic case of low-precision output, our scheme provides less impressive improvements due to information loss in the process of quantization. To improve the performance of the new detector in the quantized case, we propose a new iterative scheme that alternates multiple times between the detector and the decoder. Our simulations showed that the iterative scheme can significantly improve the bit error rate even in the quantized case.

Variational Bayesian Inference of Line Spectra

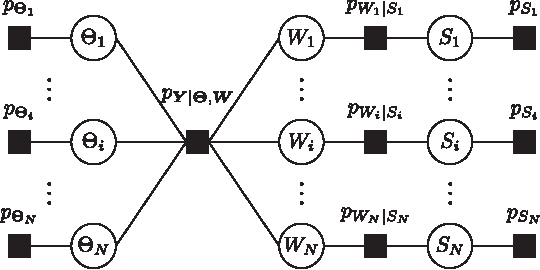
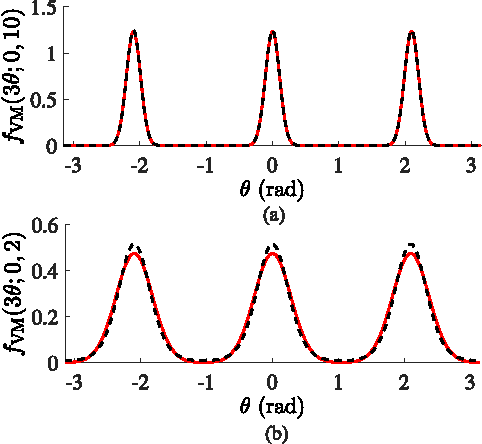
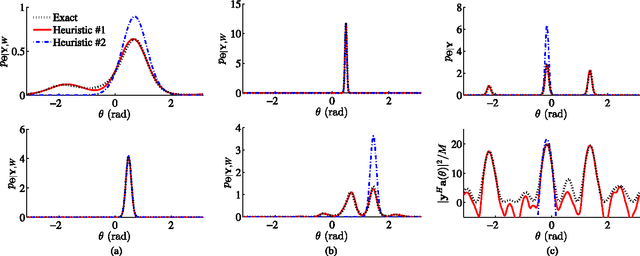
In this paper, we address the fundamental problem of line spectral estimation in a Bayesian framework. We target model order and parameter estimation via variational inference in a probabilistic model in which the frequencies are continuous-valued, i.e., not restricted to a grid; and the coefficients are governed by a Bernoulli-Gaussian prior model turning model order selection into binary sequence detection. Unlike earlier works which retain only point estimates of the frequencies, we undertake a more complete Bayesian treatment by estimating the posterior probability density functions (pdfs) of the frequencies and computing expectations over them. Thus, we additionally capture and operate with the uncertainty of the frequency estimates. Aiming to maximize the model evidence, variational optimization provides analytic approximations of the posterior pdfs and also gives estimates of the additional parameters. We propose an accurate representation of the pdfs of the frequencies by mixtures of von Mises pdfs, which yields closed-form expectations. We define the algorithm VALSE in which the estimates of the pdfs and parameters are iteratively updated. VALSE is a gridless, convergent method, does not require parameter tuning, can easily include prior knowledge about the frequencies and provides approximate posterior pdfs based on which the uncertainty in line spectral estimation can be quantified. Simulation results show that accounting for the uncertainty of frequency estimates, rather than computing just point estimates, significantly improves the performance. The performance of VALSE is superior to that of state-of-the-art methods and closely approaches the Cram\'er-Rao bound computed for the true model order.

Sparse Estimation using Bayesian Hierarchical Prior Modeling for Real and Complex Linear Models

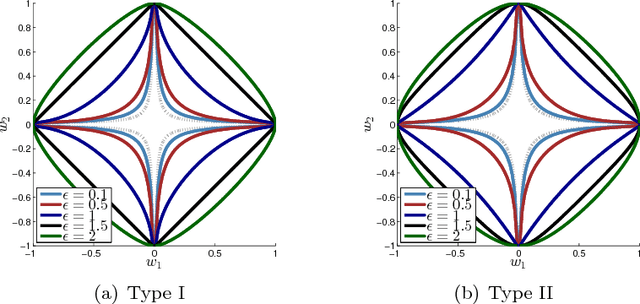
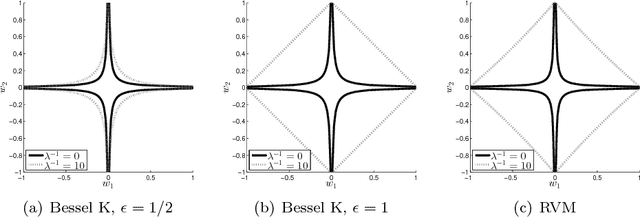
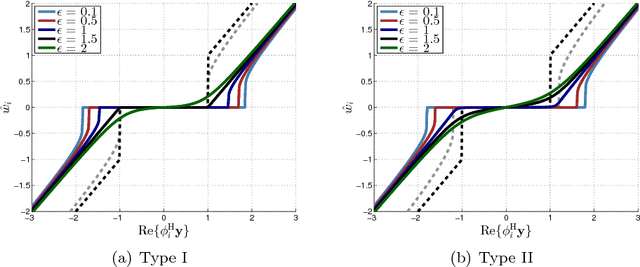
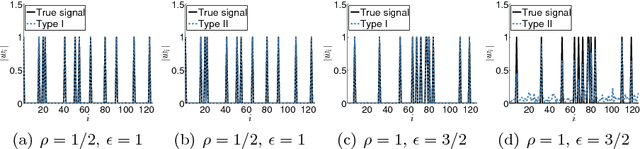
In sparse Bayesian learning (SBL), Gaussian scale mixtures (GSMs) have been used to model sparsity-inducing priors that realize a class of concave penalty functions for the regression task in real-valued signal models. Motivated by the relative scarcity of formal tools for SBL in complex-valued models, this paper proposes a GSM model - the Bessel K model - that induces concave penalty functions for the estimation of complex sparse signals. The properties of the Bessel K model are analyzed when it is applied to Type I and Type II estimation. This analysis reveals that, by tuning the parameters of the mixing pdf different penalty functions are invoked depending on the estimation type used, the value of the noise variance, and whether real or complex signals are estimated. Using the Bessel K model, we derive a sparse estimator based on a modification of the expectation-maximization algorithm formulated for Type II estimation. The estimator includes as a special instance the algorithms proposed by Tipping and Faul [1] and by Babacan et al. [2]. Numerical results show the superiority of the proposed estimator over these state-of-the-art estimators in terms of convergence speed, sparseness, reconstruction error, and robustness in low and medium signal-to-noise ratio regimes.

Message-Passing Algorithms for Channel Estimation and Decoding Using Approximate Inference

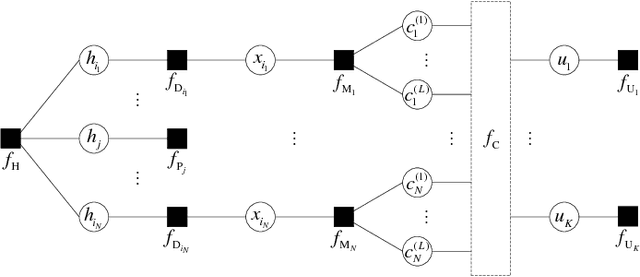
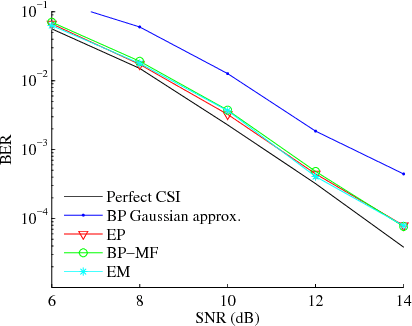
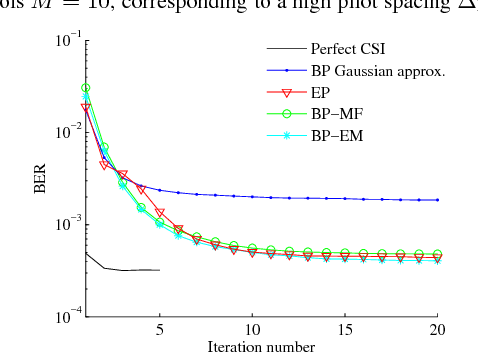
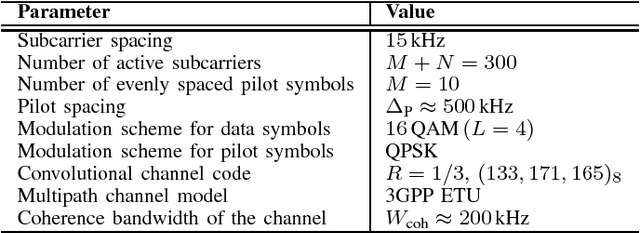
We design iterative receiver schemes for a generic wireless communication system by treating channel estimation and information decoding as an inference problem in graphical models. We introduce a recently proposed inference framework that combines belief propagation (BP) and the mean field (MF) approximation and includes these algorithms as special cases. We also show that the expectation propagation and expectation maximization algorithms can be embedded in the BP-MF framework with slight modifications. By applying the considered inference algorithms to our probabilistic model, we derive four different message-passing receiver schemes. Our numerical evaluation demonstrates that the receiver based on the BP-MF framework and its variant based on BP-EM yield the best compromise between performance, computational complexity and numerical stability among all candidate algorithms.

Merging Belief Propagation and the Mean Field Approximation: A Free Energy Approach

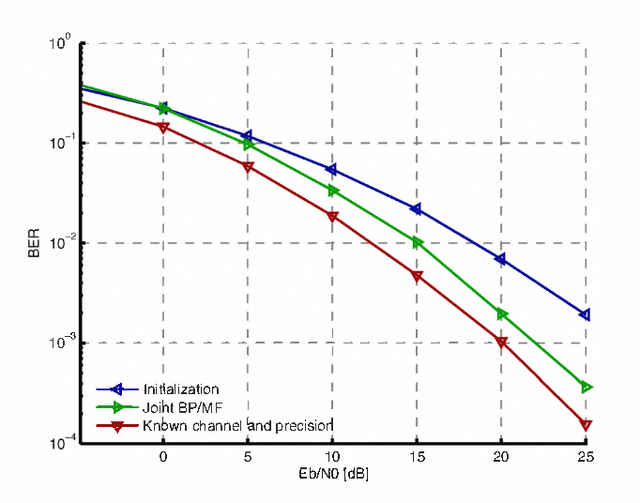
We present a joint message passing approach that combines belief propagation and the mean field approximation. Our analysis is based on the region-based free energy approximation method proposed by Yedidia et al. We show that the message passing fixed-point equations obtained with this combination correspond to stationary points of a constrained region-based free energy approximation. Moreover, we present a convergent implementation of these message passing fixedpoint equations provided that the underlying factor graph fulfills certain technical conditions. In addition, we show how to include hard constraints in the part of the factor graph corresponding to belief propagation. Finally, we demonstrate an application of our method to iterative channel estimation and decoding in an orthogonal frequency division multiplexing (OFDM) system.

Distributed Iterative Processing for Interference Channels with Receiver Cooperation

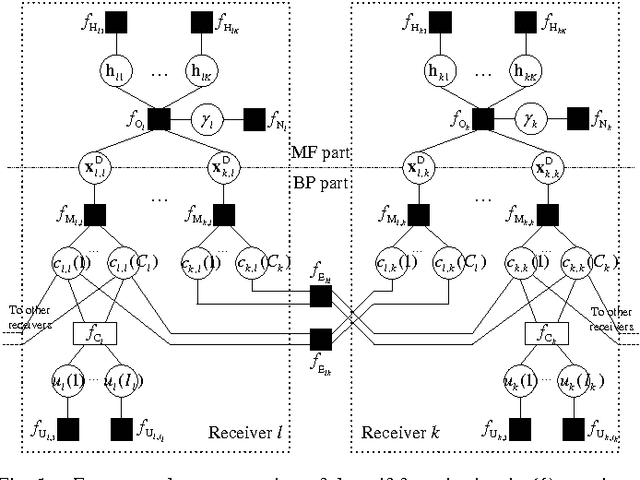
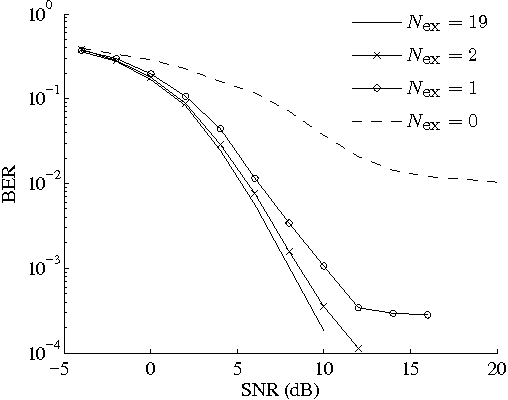
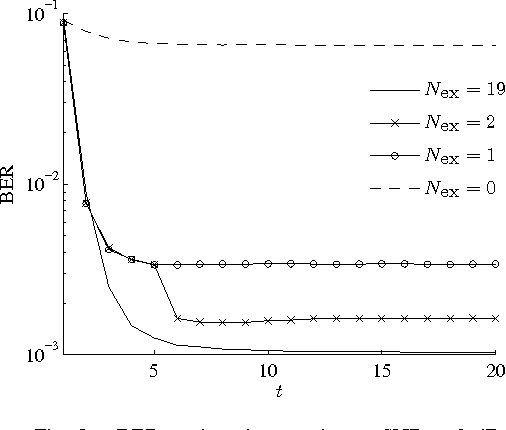
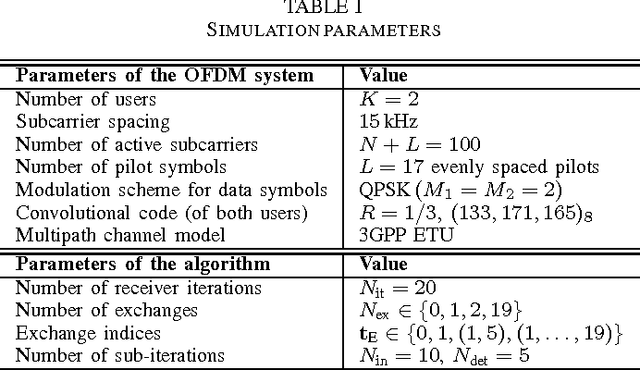
We propose a framework for the derivation and evaluation of distributed iterative algorithms for receiver cooperation in interference-limited wireless systems. Our approach views the processing within and collaboration between receivers as the solution to an inference problem in the probabilistic model of the whole system. The probabilistic model is formulated to explicitly incorporate the receivers' ability to share information of a predefined type. We employ a recently proposed unified message-passing tool to infer the variables of interest in the factor graph representation of the probabilistic model. The exchange of information between receivers arises in the form of passing messages along some specific edges of the factor graph; the rate of updating and passing these messages determines the communication overhead associated with cooperation. Simulation results illustrate the high performance of the proposed algorithm even with a low number of message exchanges between receivers.