Generating Rectifiable Measures through Neural Networks

We derive universal approximation results for the class of (countably) $m$-rectifiable measures. Specifically, we prove that $m$-rectifiable measures can be approximated as push-forwards of the one-dimensional Lebesgue measure on $[0,1]$ using ReLU neural networks with arbitrarily small approximation error in terms of Wasserstein distance. What is more, the weights in the networks under consideration are quantized and bounded and the number of ReLU neural networks required to achieve an approximation error of $\varepsilon$ is no larger than $2^{b(\varepsilon)}$ with $b(\varepsilon)=\mathcal{O}(\varepsilon^{-m}\log^2(\varepsilon))$. This result improves Lemma IX.4 in Perekrestenko et al. as it shows that the rate at which $b(\varepsilon)$ tends to infinity as $\varepsilon$ tends to zero equals the rectifiability parameter $m$, which can be much smaller than the ambient dimension. We extend this result to countably $m$-rectifiable measures and show that this rate still equals the rectifiability parameter $m$ provided that, among other technical assumptions, the measure decays exponentially on the individual components of the countably $m$-rectifiable support set.

Covering Numbers for Deep ReLU Networks with Applications to Function Approximation and Nonparametric Regression

Covering numbers of families of (deep) ReLU networks have been used to characterize their approximation-theoretic performance, upper-bound the prediction error they incur in nonparametric regression, and quantify their classification capacity. These results are based on covering number upper bounds obtained through the explicit construction of coverings. Lower bounds on covering numbers do not seem to be available in the literature. The present paper fills this gap by deriving tight (up to a multiplicative constant) lower and upper bounds on the covering numbers of fully-connected networks with bounded weights, sparse networks with bounded weights, and fully-connected networks with quantized weights. Thanks to the tightness of the bounds, a fundamental understanding of the impact of sparsity, quantization, bounded vs. unbounded weights, and network output truncation can be developed. Furthermore, the bounds allow to characterize the fundamental limits of neural network transformation, including network compression, and lead to sharp upper bounds on the prediction error in nonparametric regression through deep networks. Specifically, we can remove a $\log^6(n)$-factor in the best-known sample complexity rate in the estimation of Lipschitz functions through deep networks thereby establishing optimality. Finally, we identify a systematic relation between optimal nonparametric regression and optimal approximation through deep networks, unifying numerous results in the literature and uncovering general underlying principles.

Metric-Entropy Limits on Nonlinear Dynamical System Learning

This paper is concerned with the fundamental limits of nonlinear dynamical system learning from input-output traces. Specifically, we show that recurrent neural networks (RNNs) are capable of learning nonlinear systems that satisfy a Lipschitz property and forget past inputs fast enough in a metric-entropy optimal manner. As the sets of sequence-to-sequence maps realized by the dynamical systems we consider are significantly more massive than function classes generally considered in deep neural network approximation theory, a refined metric-entropy characterization is needed, namely in terms of order, type, and generalized dimension. We compute these quantities for the classes of exponentially-decaying and polynomially-decaying Lipschitz fading-memory systems and show that RNNs can achieve them.

Three Quantization Regimes for ReLU Networks

We establish the fundamental limits in the approximation of Lipschitz functions by deep ReLU neural networks with finite-precision weights. Specifically, three regimes, namely under-, over-, and proper quantization, in terms of minimax approximation error behavior as a function of network weight precision, are identified. This is accomplished by deriving nonasymptotic tight lower and upper bounds on the minimax approximation error. Notably, in the proper-quantization regime, neural networks exhibit memory-optimality in the approximation of Lipschitz functions. Deep networks have an inherent advantage over shallow networks in achieving memory-optimality. We also develop the notion of depth-precision tradeoff, showing that networks with high-precision weights can be converted into functionally equivalent deeper networks with low-precision weights, while preserving memory-optimality. This idea is reminiscent of sigma-delta analog-to-digital conversion, where oversampling rate is traded for resolution in the quantization of signal samples. We improve upon the best-known ReLU network approximation results for Lipschitz functions and describe a refinement of the bit extraction technique which could be of independent general interest.

Cellular automata, many-valued logic, and deep neural networks

We develop a theory characterizing the fundamental capability of deep neural networks to learn, from evolution traces, the logical rules governing the behavior of cellular automata (CA). This is accomplished by first establishing a novel connection between CA and Lukasiewicz propositional logic. While binary CA have been known for decades to essentially perform operations in Boolean logic, no such relationship exists for general CA. We demonstrate that many-valued (MV) logic, specifically Lukasiewicz propositional logic, constitutes a suitable language for characterizing general CA as logical machines. This is done by interpolating CA transition functions to continuous piecewise linear functions, which, by virtue of the McNaughton theorem, yield formulae in MV logic characterizing the CA. Recognizing that deep rectified linear unit (ReLU) networks realize continuous piecewise linear functions, it follows that these formulae are naturally extracted from CA evolution traces by deep ReLU networks. A corresponding algorithm together with a software implementation is provided. Finally, we show that the dynamical behavior of CA can be realized by recurrent neural networks.

Extracting Formulae in Many-Valued Logic from Deep Neural Networks

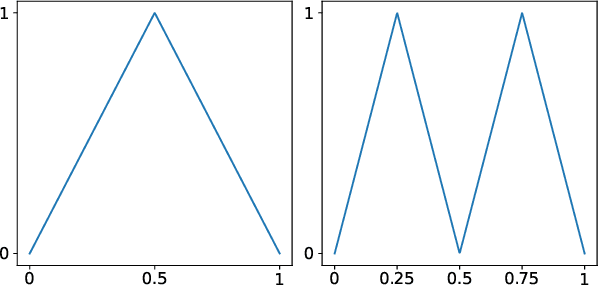
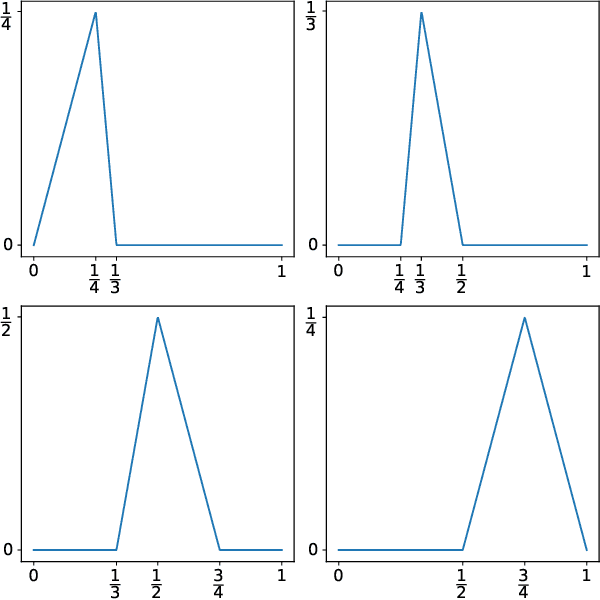
We propose a new perspective on deep ReLU networks, namely as circuit counterparts of Lukasiewicz infinite-valued logic -- a many-valued (MV) generalization of Boolean logic. An algorithm for extracting formulae in MV logic from deep ReLU networks is presented. As the algorithm applies to networks with general, in particular also real-valued, weights, it can be used to extract logical formulae from deep ReLU networks trained on data.

High-Dimensional Distribution Generation Through Deep Neural Networks

We show that every $d$-dimensional probability distribution of bounded support can be generated through deep ReLU networks out of a $1$-dimensional uniform input distribution. What is more, this is possible without incurring a cost - in terms of approximation error measured in Wasserstein-distance - relative to generating the $d$-dimensional target distribution from $d$ independent random variables. This is enabled by a vast generalization of the space-filling approach discovered in (Bailey & Telgarsky, 2018). The construction we propose elicits the importance of network depth in driving the Wasserstein distance between the target distribution and its neural network approximation to zero. Finally, we find that, for histogram target distributions, the number of bits needed to encode the corresponding generative network equals the fundamental limit for encoding probability distributions as dictated by quantization theory.

Metric Entropy Limits on Recurrent Neural Network Learning of Linear Dynamical Systems

One of the most influential results in neural network theory is the universal approximation theorem [1, 2, 3] which states that continuous functions can be approximated to within arbitrary accuracy by single-hidden-layer feedforward neural networks. The purpose of this paper is to establish a result in this spirit for the approximation of general discrete-time linear dynamical systems - including time-varying systems - by recurrent neural networks (RNNs). For the subclass of linear time-invariant (LTI) systems, we devise a quantitative version of this statement. Specifically, measuring the complexity of the considered class of LTI systems through metric entropy according to [4], we show that RNNs can optimally learn - or identify in system-theory parlance - stable LTI systems. For LTI systems whose input-output relation is characterized through a difference equation, this means that RNNs can learn the difference equation from input-output traces in a metric-entropy optimal manner.

Constructive Universal High-Dimensional Distribution Generation through Deep ReLU Networks

We present an explicit deep neural network construction that transforms uniformly distributed one-dimensional noise into an arbitrarily close approximation of any two-dimensional Lipschitz-continuous target distribution. The key ingredient of our design is a generalization of the "space-filling" property of sawtooth functions discovered in (Bailey & Telgarsky, 2018). We elicit the importance of depth - in our neural network construction - in driving the Wasserstein distance between the target distribution and the approximation realized by the network to zero. An extension to output distributions of arbitrary dimension is outlined. Finally, we show that the proposed construction does not incur a cost - in terms of error measured in Wasserstein-distance - relative to generating $d$-dimensional target distributions from $d$ independent random variables.

Affine Symmetries and Neural Network Identifiability

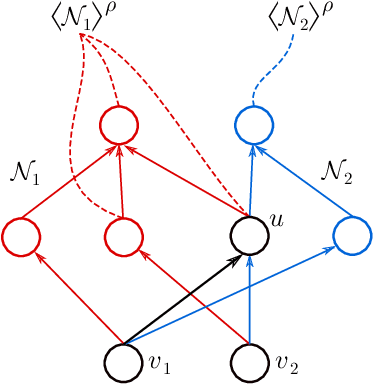
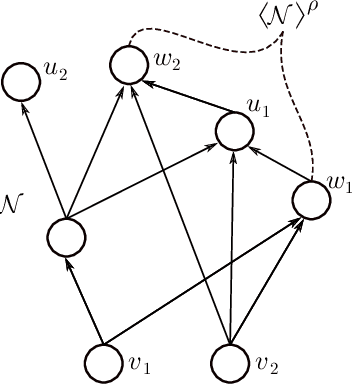
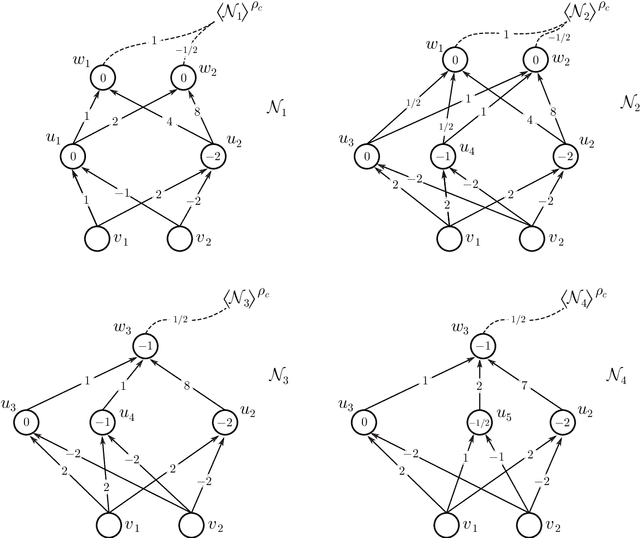
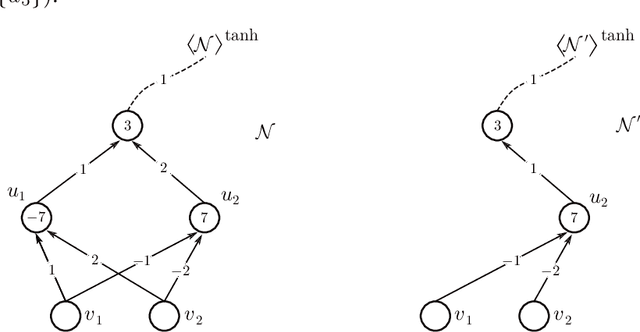
We address the following question of neural network identifiability: Suppose we are given a function $f:\mathbb{R}^m\to\mathbb{R}^n$ and a nonlinearity $\rho$. Can we specify the architecture, weights, and biases of all feed-forward neural networks with respect to $\rho$ giving rise to $f$? Existing literature on the subject suggests that the answer should be yes, provided we are only concerned with finding networks that satisfy certain "genericity conditions". Moreover, the identified networks are mutually related by symmetries of the nonlinearity. For instance, the $\tanh$ function is odd, and so flipping the signs of the incoming and outgoing weights of a neuron does not change the output map of the network. The results known hitherto, however, apply either to single-layer networks, or to networks satisfying specific structural assumptions (such as full connectivity), as well as to specific nonlinearities. In an effort to answer the identifiability question in greater generality, we consider arbitrary nonlinearities with potentially complicated affine symmetries, and we show that the symmetries can be used to find a rich set of networks giving rise to the same function $f$. The set obtained in this manner is, in fact, exhaustive (i.e., it contains all networks giving rise to $f$) unless there exists a network $\mathcal{A}$ "with no internal symmetries" giving rise to the identically zero function. This result can thus be interpreted as an analog of the rank-nullity theorem for linear operators. We furthermore exhibit a class of "$\tanh$-type" nonlinearities (including the tanh function itself) for which such a network $\mathcal{A}$ does not exist, thereby solving the identifiability question for these nonlinearities in full generality. Finally, we show that this class contains nonlinearities with arbitrarily complicated symmetries.