Covering Numbers for Deep ReLU Networks with Applications to Function Approximation and Nonparametric Regression

Covering numbers of families of (deep) ReLU networks have been used to characterize their approximation-theoretic performance, upper-bound the prediction error they incur in nonparametric regression, and quantify their classification capacity. These results are based on covering number upper bounds obtained through the explicit construction of coverings. Lower bounds on covering numbers do not seem to be available in the literature. The present paper fills this gap by deriving tight (up to a multiplicative constant) lower and upper bounds on the covering numbers of fully-connected networks with bounded weights, sparse networks with bounded weights, and fully-connected networks with quantized weights. Thanks to the tightness of the bounds, a fundamental understanding of the impact of sparsity, quantization, bounded vs. unbounded weights, and network output truncation can be developed. Furthermore, the bounds allow to characterize the fundamental limits of neural network transformation, including network compression, and lead to sharp upper bounds on the prediction error in nonparametric regression through deep networks. Specifically, we can remove a $\log^6(n)$-factor in the best-known sample complexity rate in the estimation of Lipschitz functions through deep networks thereby establishing optimality. Finally, we identify a systematic relation between optimal nonparametric regression and optimal approximation through deep networks, unifying numerous results in the literature and uncovering general underlying principles.

Three Quantization Regimes for ReLU Networks

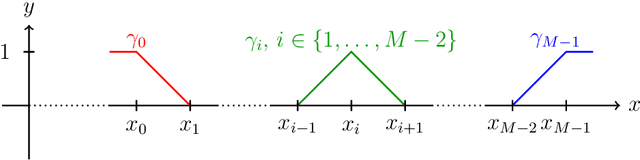
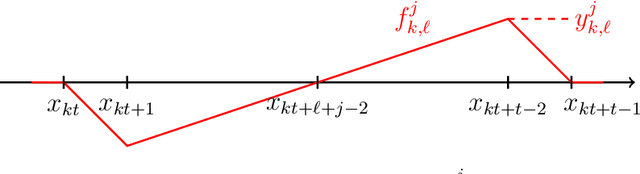
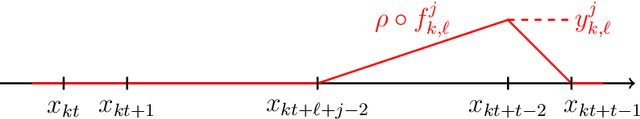
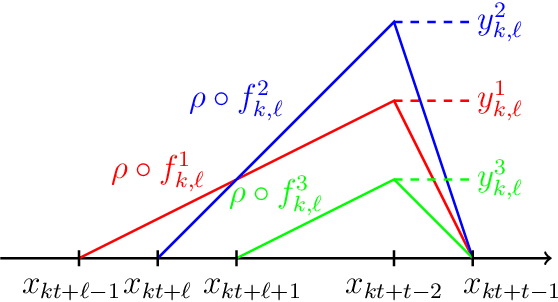
We establish the fundamental limits in the approximation of Lipschitz functions by deep ReLU neural networks with finite-precision weights. Specifically, three regimes, namely under-, over-, and proper quantization, in terms of minimax approximation error behavior as a function of network weight precision, are identified. This is accomplished by deriving nonasymptotic tight lower and upper bounds on the minimax approximation error. Notably, in the proper-quantization regime, neural networks exhibit memory-optimality in the approximation of Lipschitz functions. Deep networks have an inherent advantage over shallow networks in achieving memory-optimality. We also develop the notion of depth-precision tradeoff, showing that networks with high-precision weights can be converted into functionally equivalent deeper networks with low-precision weights, while preserving memory-optimality. This idea is reminiscent of sigma-delta analog-to-digital conversion, where oversampling rate is traded for resolution in the quantization of signal samples. We improve upon the best-known ReLU network approximation results for Lipschitz functions and describe a refinement of the bit extraction technique which could be of independent general interest.