Three Quantization Regimes for ReLU Networks
Paper and Code
May 03, 2024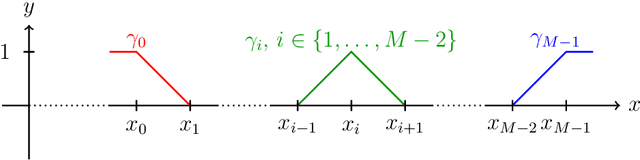
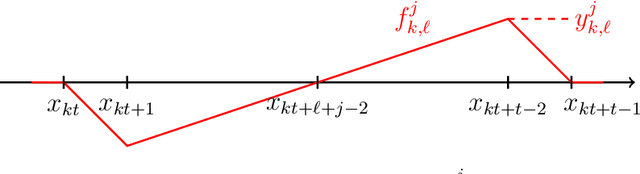
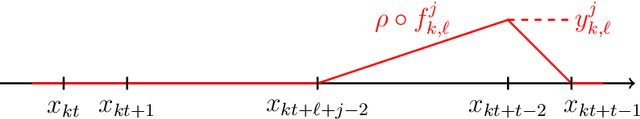
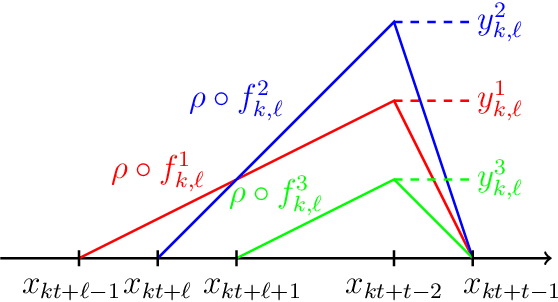
We establish the fundamental limits in the approximation of Lipschitz functions by deep ReLU neural networks with finite-precision weights. Specifically, three regimes, namely under-, over-, and proper quantization, in terms of minimax approximation error behavior as a function of network weight precision, are identified. This is accomplished by deriving nonasymptotic tight lower and upper bounds on the minimax approximation error. Notably, in the proper-quantization regime, neural networks exhibit memory-optimality in the approximation of Lipschitz functions. Deep networks have an inherent advantage over shallow networks in achieving memory-optimality. We also develop the notion of depth-precision tradeoff, showing that networks with high-precision weights can be converted into functionally equivalent deeper networks with low-precision weights, while preserving memory-optimality. This idea is reminiscent of sigma-delta analog-to-digital conversion, where oversampling rate is traded for resolution in the quantization of signal samples. We improve upon the best-known ReLU network approximation results for Lipschitz functions and describe a refinement of the bit extraction technique which could be of independent general interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge