The mathematics of adversarial attacks in AI -- Why deep learning is unstable despite the existence of stable neural networks

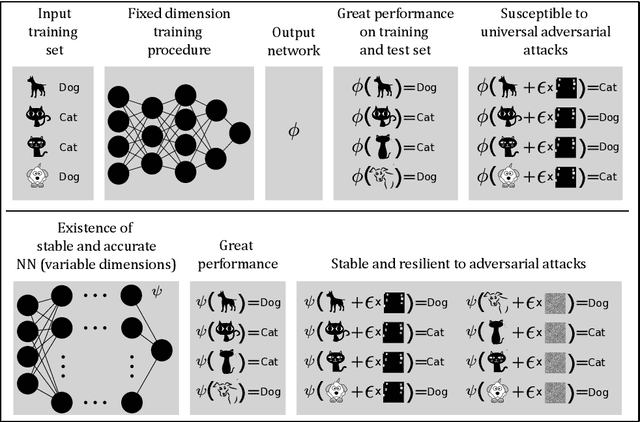
The unprecedented success of deep learning (DL) makes it unchallenged when it comes to classification problems. However, it is well established that the current DL methodology produces universally unstable neural networks (NNs). The instability problem has caused an enormous research effort -- with a vast literature on so-called adversarial attacks -- yet there has been no solution to the problem. Our paper addresses why there has been no solution to the problem, as we prove the following mathematical paradox: any training procedure based on training neural networks for classification problems with a fixed architecture will yield neural networks that are either inaccurate or unstable (if accurate) -- despite the provable existence of both accurate and stable neural networks for the same classification problems. The key is that the stable and accurate neural networks must have variable dimensions depending on the input, in particular, variable dimensions is a necessary condition for stability. Our result points towards the paradox that accurate and stable neural networks exist, however, modern algorithms do not compute them. This yields the question: if the existence of neural networks with desirable properties can be proven, can one also find algorithms that compute them? There are cases in mathematics where provable existence implies computability, but will this be the case for neural networks? The contrary is true, as we demonstrate how neural networks can provably exist as approximate minimisers to standard optimisation problems with standard cost functions, however, no randomised algorithm can compute them with probability better than 1/2.

Affine Symmetries and Neural Network Identifiability

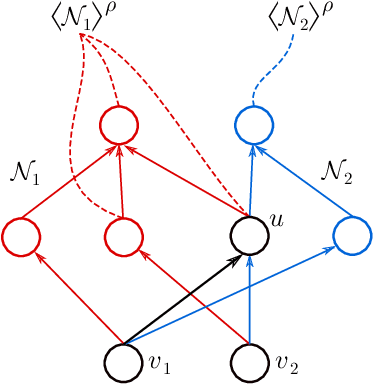
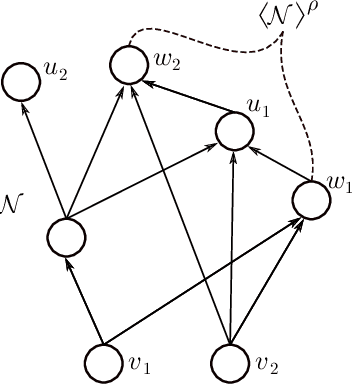
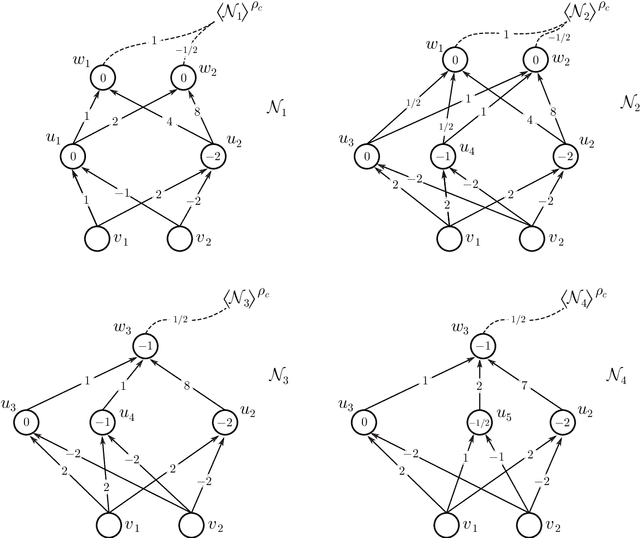
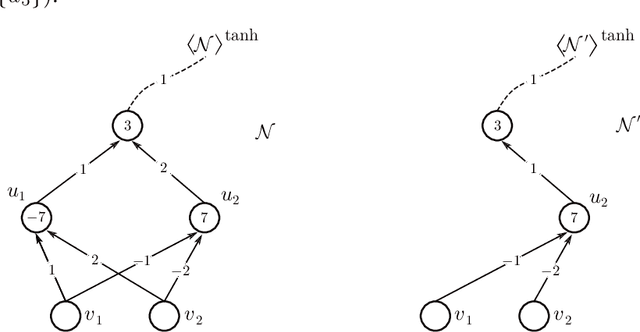
We address the following question of neural network identifiability: Suppose we are given a function $f:\mathbb{R}^m\to\mathbb{R}^n$ and a nonlinearity $\rho$. Can we specify the architecture, weights, and biases of all feed-forward neural networks with respect to $\rho$ giving rise to $f$? Existing literature on the subject suggests that the answer should be yes, provided we are only concerned with finding networks that satisfy certain "genericity conditions". Moreover, the identified networks are mutually related by symmetries of the nonlinearity. For instance, the $\tanh$ function is odd, and so flipping the signs of the incoming and outgoing weights of a neuron does not change the output map of the network. The results known hitherto, however, apply either to single-layer networks, or to networks satisfying specific structural assumptions (such as full connectivity), as well as to specific nonlinearities. In an effort to answer the identifiability question in greater generality, we consider arbitrary nonlinearities with potentially complicated affine symmetries, and we show that the symmetries can be used to find a rich set of networks giving rise to the same function $f$. The set obtained in this manner is, in fact, exhaustive (i.e., it contains all networks giving rise to $f$) unless there exists a network $\mathcal{A}$ "with no internal symmetries" giving rise to the identically zero function. This result can thus be interpreted as an analog of the rank-nullity theorem for linear operators. We furthermore exhibit a class of "$\tanh$-type" nonlinearities (including the tanh function itself) for which such a network $\mathcal{A}$ does not exist, thereby solving the identifiability question for these nonlinearities in full generality. Finally, we show that this class contains nonlinearities with arbitrarily complicated symmetries.

Neural network identifiability for a family of sigmoidal nonlinearities

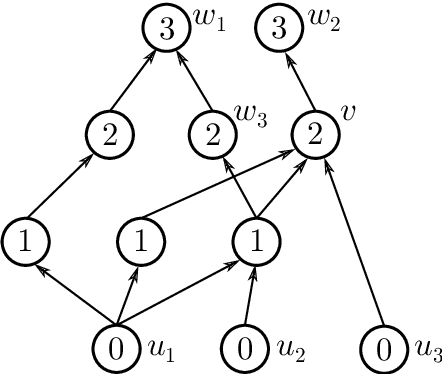
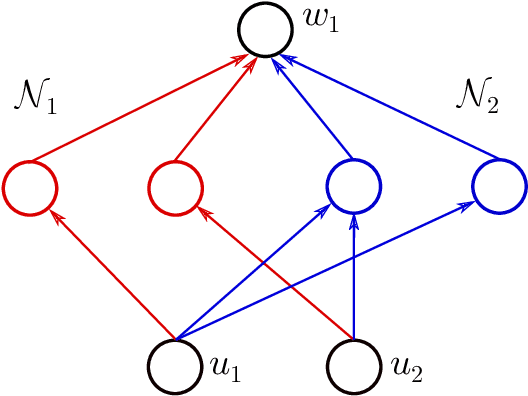
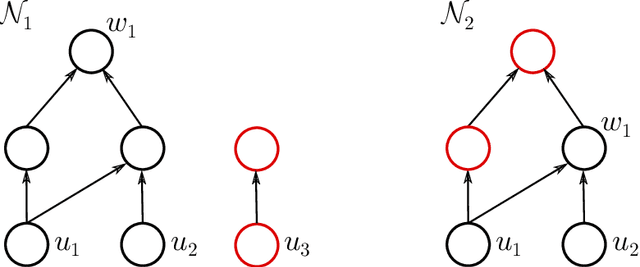
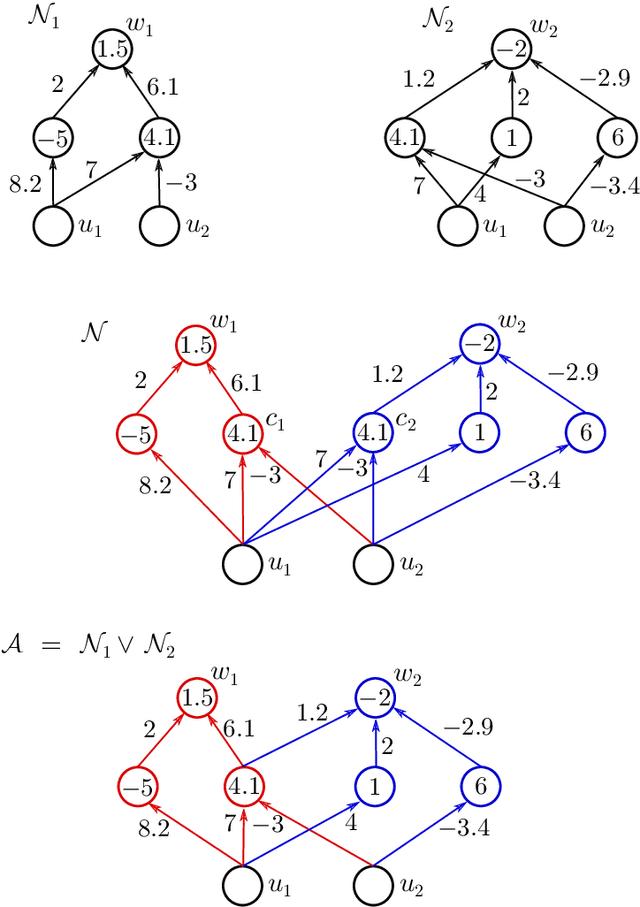
This paper addresses the following question of neural network identifiability: Does the input-output map realized by a feed-forward neural network with respect to a given nonlinearity uniquely specify the network architecture, weights, and biases? Existing literature on the subject Sussman 1992, Albertini, Sontag et al. 1993, Fefferman 1994 suggests that the answer should be yes, up to certain symmetries induced by the nonlinearity, and provided the networks under consideration satisfy certain "genericity conditions". The results in Sussman 1992 and Albertini, Sontag et al. 1993 apply to networks with a single hidden layer and in Fefferman 1994 the networks need to be fully connected. In an effort to answer the identifiability question in greater generality, we derive necessary genericity conditions for the identifiability of neural networks of arbitrary depth and connectivity with an arbitrary nonlinearity. Moreover, we construct a family of nonlinearities for which these genericity conditions are minimal, i.e., both necessary and sufficient. This family is large enough to approximate many commonly encountered nonlinearities to arbitrary precision in the uniform norm.