Affine Symmetries and Neural Network Identifiability

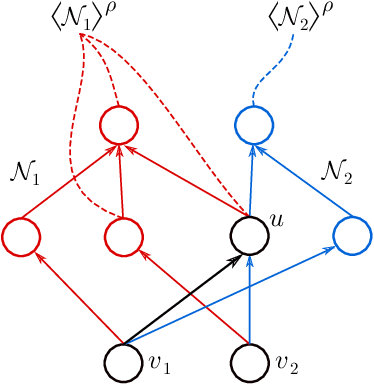
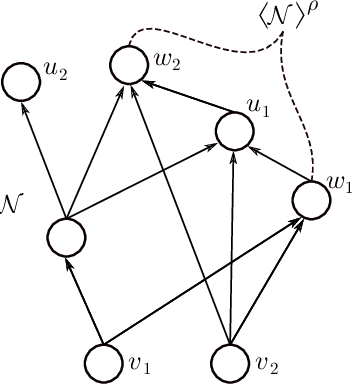
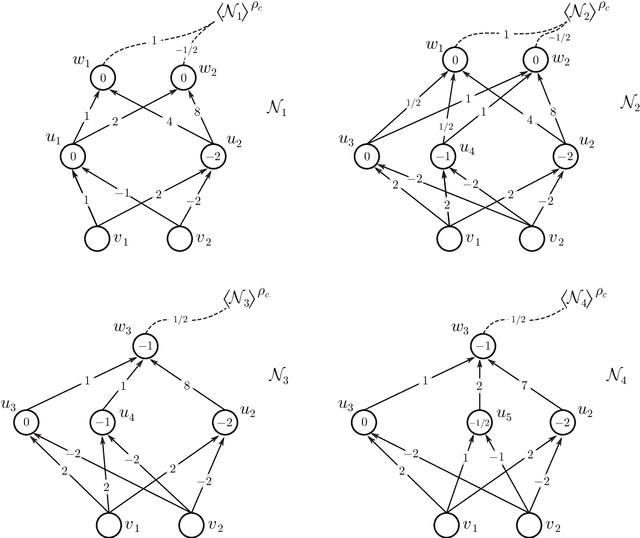
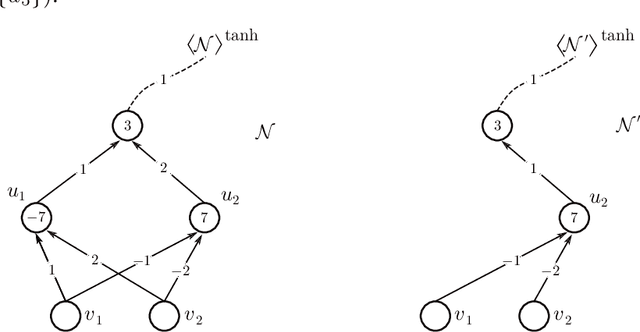
We address the following question of neural network identifiability: Suppose we are given a function $f:\mathbb{R}^m\to\mathbb{R}^n$ and a nonlinearity $\rho$. Can we specify the architecture, weights, and biases of all feed-forward neural networks with respect to $\rho$ giving rise to $f$? Existing literature on the subject suggests that the answer should be yes, provided we are only concerned with finding networks that satisfy certain "genericity conditions". Moreover, the identified networks are mutually related by symmetries of the nonlinearity. For instance, the $\tanh$ function is odd, and so flipping the signs of the incoming and outgoing weights of a neuron does not change the output map of the network. The results known hitherto, however, apply either to single-layer networks, or to networks satisfying specific structural assumptions (such as full connectivity), as well as to specific nonlinearities. In an effort to answer the identifiability question in greater generality, we consider arbitrary nonlinearities with potentially complicated affine symmetries, and we show that the symmetries can be used to find a rich set of networks giving rise to the same function $f$. The set obtained in this manner is, in fact, exhaustive (i.e., it contains all networks giving rise to $f$) unless there exists a network $\mathcal{A}$ "with no internal symmetries" giving rise to the identically zero function. This result can thus be interpreted as an analog of the rank-nullity theorem for linear operators. We furthermore exhibit a class of "$\tanh$-type" nonlinearities (including the tanh function itself) for which such a network $\mathcal{A}$ does not exist, thereby solving the identifiability question for these nonlinearities in full generality. Finally, we show that this class contains nonlinearities with arbitrarily complicated symmetries.