On the consistent reasoning paradox of intelligence and optimal trust in AI: The power of 'I don't know'

We introduce the Consistent Reasoning Paradox (CRP). Consistent reasoning, which lies at the core of human intelligence, is the ability to handle tasks that are equivalent, yet described by different sentences ('Tell me the time!' and 'What is the time?'). The CRP asserts that consistent reasoning implies fallibility -- in particular, human-like intelligence in AI necessarily comes with human-like fallibility. Specifically, it states that there are problems, e.g. in basic arithmetic, where any AI that always answers and strives to mimic human intelligence by reasoning consistently will hallucinate (produce wrong, yet plausible answers) infinitely often. The paradox is that there exists a non-consistently reasoning AI (which therefore cannot be on the level of human intelligence) that will be correct on the same set of problems. The CRP also shows that detecting these hallucinations, even in a probabilistic sense, is strictly harder than solving the original problems, and that there are problems that an AI may answer correctly, but it cannot provide a correct logical explanation for how it arrived at the answer. Therefore, the CRP implies that any trustworthy AI (i.e., an AI that never answers incorrectly) that also reasons consistently must be able to say 'I don't know'. Moreover, this can only be done by implicitly computing a new concept that we introduce, termed the 'I don't know' function -- something currently lacking in modern AI. In view of these insights, the CRP also provides a glimpse into the behaviour of Artificial General Intelligence (AGI). An AGI cannot be 'almost sure', nor can it always explain itself, and therefore to be trustworthy it must be able to say 'I don't know'.

Stealth edits for provably fixing or attacking large language models

We reveal new methods and the theoretical foundations of techniques for editing large language models. We also show how the new theory can be used to assess the editability of models and to expose their susceptibility to previously unknown malicious attacks. Our theoretical approach shows that a single metric (a specific measure of the intrinsic dimensionality of the model's features) is fundamental to predicting the success of popular editing approaches, and reveals new bridges between disparate families of editing methods. We collectively refer to these approaches as stealth editing methods, because they aim to directly and inexpensively update a model's weights to correct the model's responses to known hallucinating prompts without otherwise affecting the model's behaviour, without requiring retraining. By carefully applying the insight gleaned from our theoretical investigation, we are able to introduce a new network block -- named a jet-pack block -- which is optimised for highly selective model editing, uses only standard network operations, and can be inserted into existing networks. The intrinsic dimensionality metric also determines the vulnerability of a language model to a stealth attack: a small change to a model's weights which changes its response to a single attacker-chosen prompt. Stealth attacks do not require access to or knowledge of the model's training data, therefore representing a potent yet previously unrecognised threat to redistributed foundation models. They are computationally simple enough to be implemented in malware in many cases. Extensive experimental results illustrate and support the method and its theoretical underpinnings. Demos and source code for editing language models are available at https://github.com/qinghua-zhou/stealth-edits.

When can you trust feature selection? -- I: A condition-based analysis of LASSO and generalised hardness of approximation

The arrival of AI techniques in computations, with the potential for hallucinations and non-robustness, has made trustworthiness of algorithms a focal point. However, trustworthiness of the many classical approaches are not well understood. This is the case for feature selection, a classical problem in the sciences, statistics, machine learning etc. Here, the LASSO optimisation problem is standard. Despite its widespread use, it has not been established when the output of algorithms attempting to compute support sets of minimisers of LASSO in order to do feature selection can be trusted. In this paper we establish how no (randomised) algorithm that works on all inputs can determine the correct support sets (with probability $> 1/2$) of minimisers of LASSO when reading approximate input, regardless of precision and computing power. However, we define a LASSO condition number and design an efficient algorithm for computing these support sets provided the input data is well-posed (has finite condition number) in time polynomial in the dimensions and logarithm of the condition number. For ill-posed inputs the algorithm runs forever, hence, it will never produce a wrong answer. Furthermore, the algorithm computes an upper bound for the condition number when this is finite. Finally, for any algorithm defined on an open set containing a point with infinite condition number, there is an input for which the algorithm will either run forever or produce a wrong answer. Our impossibility results stem from generalised hardness of approximation -- within the Solvability Complexity Index (SCI) hierarchy framework -- that generalises the classical phenomenon of hardness of approximation.

The Boundaries of Verifiable Accuracy, Robustness, and Generalisation in Deep Learning

In this work, we assess the theoretical limitations of determining guaranteed stability and accuracy of neural networks in classification tasks. We consider classical distribution-agnostic framework and algorithms minimising empirical risks and potentially subjected to some weights regularisation. We show that there is a large family of tasks for which computing and verifying ideal stable and accurate neural networks in the above settings is extremely challenging, if at all possible, even when such ideal solutions exist within the given class of neural architectures.

How adversarial attacks can disrupt seemingly stable accurate classifiers

Adversarial attacks dramatically change the output of an otherwise accurate learning system using a seemingly inconsequential modification to a piece of input data. Paradoxically, empirical evidence indicates that even systems which are robust to large random perturbations of the input data remain susceptible to small, easily constructed, adversarial perturbations of their inputs. Here, we show that this may be seen as a fundamental feature of classifiers working with high dimensional input data. We introduce a simple generic and generalisable framework for which key behaviours observed in practical systems arise with high probability -- notably the simultaneous susceptibility of the (otherwise accurate) model to easily constructed adversarial attacks, and robustness to random perturbations of the input data. We confirm that the same phenomena are directly observed in practical neural networks trained on standard image classification problems, where even large additive random noise fails to trigger the adversarial instability of the network. A surprising takeaway is that even small margins separating a classifier's decision surface from training and testing data can hide adversarial susceptibility from being detected using randomly sampled perturbations. Counterintuitively, using additive noise during training or testing is therefore inefficient for eradicating or detecting adversarial examples, and more demanding adversarial training is required.

The mathematics of adversarial attacks in AI -- Why deep learning is unstable despite the existence of stable neural networks

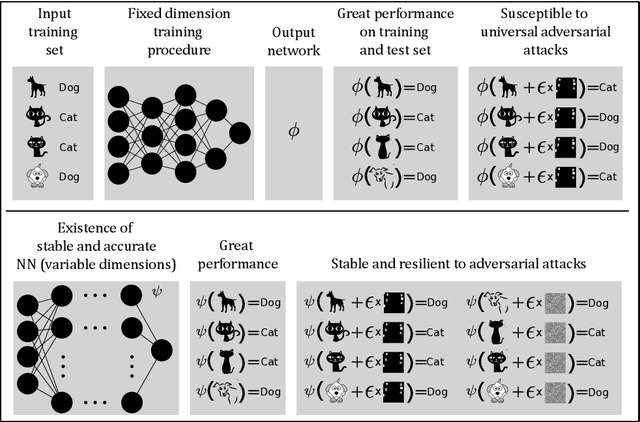
The unprecedented success of deep learning (DL) makes it unchallenged when it comes to classification problems. However, it is well established that the current DL methodology produces universally unstable neural networks (NNs). The instability problem has caused an enormous research effort -- with a vast literature on so-called adversarial attacks -- yet there has been no solution to the problem. Our paper addresses why there has been no solution to the problem, as we prove the following mathematical paradox: any training procedure based on training neural networks for classification problems with a fixed architecture will yield neural networks that are either inaccurate or unstable (if accurate) -- despite the provable existence of both accurate and stable neural networks for the same classification problems. The key is that the stable and accurate neural networks must have variable dimensions depending on the input, in particular, variable dimensions is a necessary condition for stability. Our result points towards the paradox that accurate and stable neural networks exist, however, modern algorithms do not compute them. This yields the question: if the existence of neural networks with desirable properties can be proven, can one also find algorithms that compute them? There are cases in mathematics where provable existence implies computability, but will this be the case for neural networks? The contrary is true, as we demonstrate how neural networks can provably exist as approximate minimisers to standard optimisation problems with standard cost functions, however, no randomised algorithm can compute them with probability better than 1/2.