Qinghua Zhou
Staining and locking computer vision models without retraining
Jul 29, 2025Abstract:We introduce new methods of staining and locking computer vision models, to protect their owners' intellectual property. Staining, also known as watermarking, embeds secret behaviour into a model which can later be used to identify it, while locking aims to make a model unusable unless a secret trigger is inserted into input images. Unlike existing methods, our algorithms can be used to stain and lock pre-trained models without requiring fine-tuning or retraining, and come with provable, computable guarantees bounding their worst-case false positive rates. The stain and lock are implemented by directly modifying a small number of the model's weights and have minimal impact on the (unlocked) model's performance. Locked models are unlocked by inserting a small `trigger patch' into the corner of the input image. We present experimental results showing the efficacy of our methods and demonstrating their practical performance on a variety of computer vision models.
StepProof: Step-by-step verification of natural language mathematical proofs
Jun 12, 2025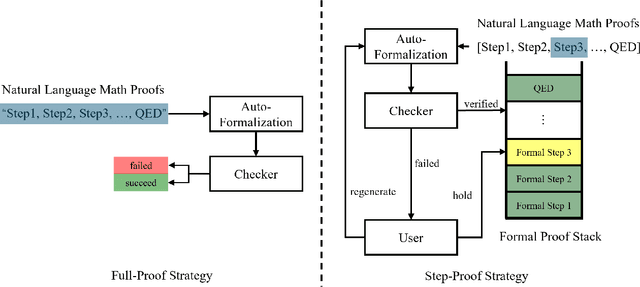

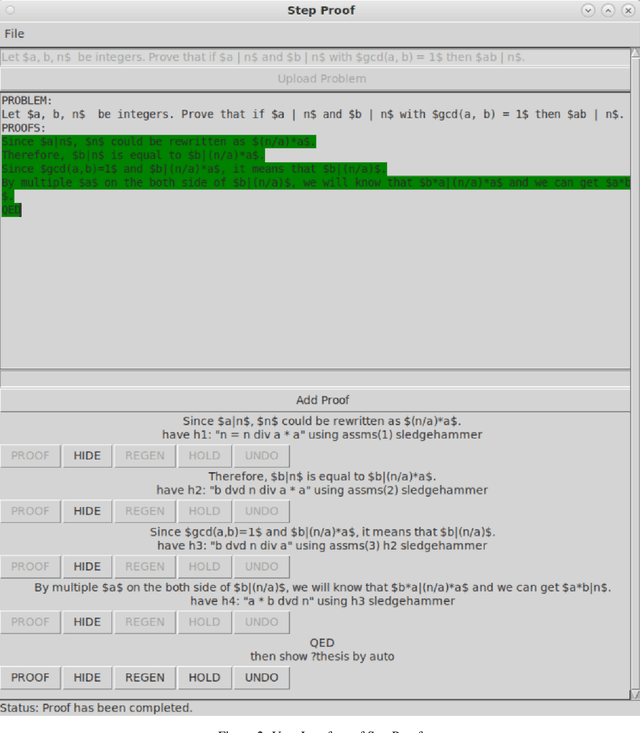

Abstract:Interactive theorem provers (ITPs) are powerful tools for the formal verification of mathematical proofs down to the axiom level. However, their lack of a natural language interface remains a significant limitation. Recent advancements in large language models (LLMs) have enhanced the understanding of natural language inputs, paving the way for autoformalization - the process of translating natural language proofs into formal proofs that can be verified. Despite these advancements, existing autoformalization approaches are limited to verifying complete proofs and lack the capability for finer, sentence-level verification. To address this gap, we propose StepProof, a novel autoformalization method designed for granular, step-by-step verification. StepProof breaks down complete proofs into multiple verifiable subproofs, enabling sentence-level verification. Experimental results demonstrate that StepProof significantly improves proof success rates and efficiency compared to traditional methods. Additionally, we found that minor manual adjustments to the natural language proofs, tailoring them for step-level verification, further enhanced StepProof's performance in autoformalization.
MSCCL++: Rethinking GPU Communication Abstractions for Cutting-edge AI Applications
Apr 11, 2025

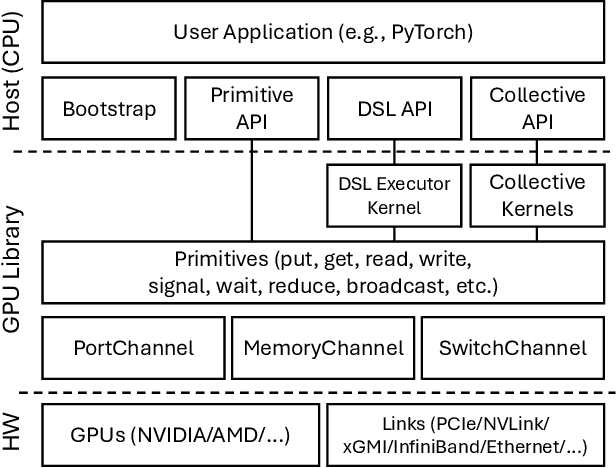
Abstract:Modern cutting-edge AI applications are being developed over fast-evolving, heterogeneous, nascent hardware devices. This requires frequent reworking of the AI software stack to adopt bottom-up changes from new hardware, which takes time for general-purpose software libraries. Consequently, real applications often develop custom software stacks optimized for their specific workloads and hardware. Custom stacks help quick development and optimization, but incur a lot of redundant efforts across applications in writing non-portable code. This paper discusses an alternative communication library interface for AI applications that offers both portability and performance by reducing redundant efforts while maintaining flexibility for customization. We present MSCCL++, a novel abstraction of GPU communication based on separation of concerns: (1) a primitive interface provides a minimal hardware abstraction as a common ground for software and hardware developers to write custom communication, and (2) higher-level portable interfaces and specialized implementations enable optimization for different hardware environments. This approach makes the primitive interface reusable across applications while enabling highly flexible optimization. Compared to state-of-the-art baselines (NCCL, RCCL, and MSCCL), MSCCL++ achieves speedups of up to 3.8$\times$ for collective communication and up to 15\% for real-world AI inference workloads. MSCCL++ is in production of multiple AI services provided by Microsoft Azure, and is also adopted by RCCL, the GPU collective communication library maintained by AMD. MSCCL++ is open-source and available at https://github.com/microsoft/mscclpp.
Accelerating Large Language Model Training with Hybrid GPU-based Compression
Sep 04, 2024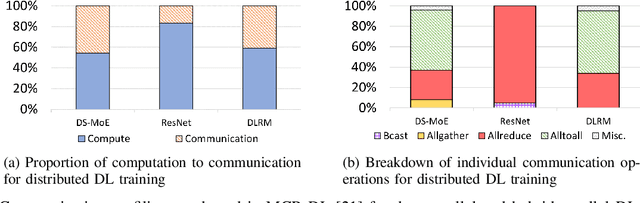
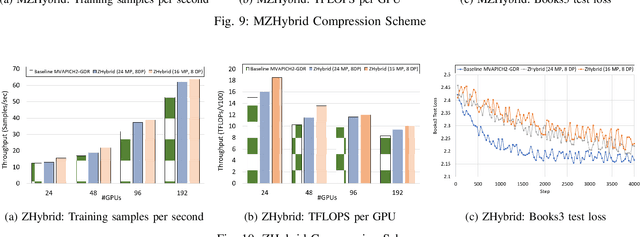
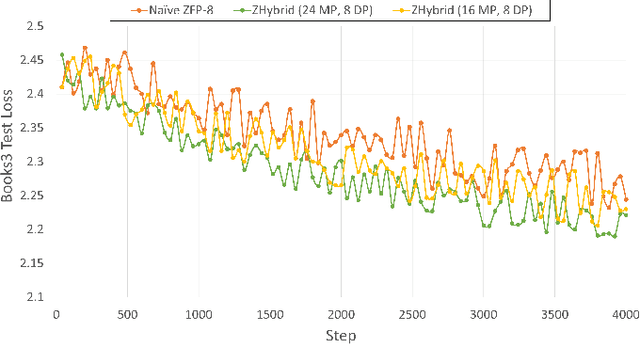
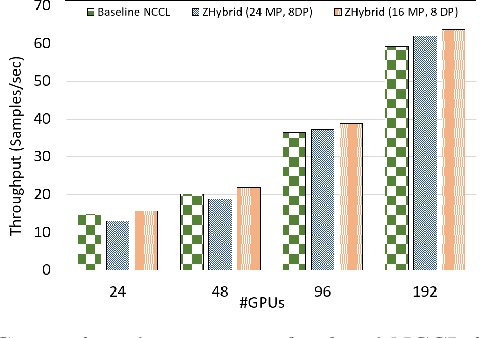
Abstract:Data Parallelism (DP), Tensor Parallelism (TP), and Pipeline Parallelism (PP) are the three strategies widely adopted to enable fast and efficient Large Language Model (LLM) training. However, these approaches rely on data-intensive communication routines to collect, aggregate, and re-distribute gradients, activations, and other important model information, which pose significant overhead. Co-designed with GPU-based compression libraries, MPI libraries have been proven to reduce message size significantly, and leverage interconnect bandwidth, thus increasing training efficiency while maintaining acceptable accuracy. In this work, we investigate the efficacy of compression-assisted MPI collectives under the context of distributed LLM training using 3D parallelism and ZeRO optimizations. We scaled up to 192 V100 GPUs on the Lassen supercomputer. First, we enabled a na\"ive compression scheme across all collectives and observed a 22.5\% increase in TFLOPS per GPU and a 23.6\% increase in samples per second for GPT-NeoX-20B training. Nonetheless, such a strategy ignores the sparsity discrepancy among messages communicated in each parallelism degree, thus introducing more errors and causing degradation in training loss. Therefore, we incorporated hybrid compression settings toward each parallel dimension and adjusted the compression intensity accordingly. Given their low-rank structure (arXiv:2301.02654), we apply aggressive compression on gradients when performing DP All-reduce. We adopt milder compression to preserve precision while communicating activations, optimizer states, and model parameters in TP and PP. Using the adjusted hybrid compression scheme, we demonstrate a 17.3\% increase in TFLOPS per GPU and a 12.7\% increase in samples per second while reaching baseline loss convergence.
Stealth edits for provably fixing or attacking large language models
Jun 18, 2024



Abstract:We reveal new methods and the theoretical foundations of techniques for editing large language models. We also show how the new theory can be used to assess the editability of models and to expose their susceptibility to previously unknown malicious attacks. Our theoretical approach shows that a single metric (a specific measure of the intrinsic dimensionality of the model's features) is fundamental to predicting the success of popular editing approaches, and reveals new bridges between disparate families of editing methods. We collectively refer to these approaches as stealth editing methods, because they aim to directly and inexpensively update a model's weights to correct the model's responses to known hallucinating prompts without otherwise affecting the model's behaviour, without requiring retraining. By carefully applying the insight gleaned from our theoretical investigation, we are able to introduce a new network block -- named a jet-pack block -- which is optimised for highly selective model editing, uses only standard network operations, and can be inserted into existing networks. The intrinsic dimensionality metric also determines the vulnerability of a language model to a stealth attack: a small change to a model's weights which changes its response to a single attacker-chosen prompt. Stealth attacks do not require access to or knowledge of the model's training data, therefore representing a potent yet previously unrecognised threat to redistributed foundation models. They are computationally simple enough to be implemented in malware in many cases. Extensive experimental results illustrate and support the method and its theoretical underpinnings. Demos and source code for editing language models are available at https://github.com/qinghua-zhou/stealth-edits.
Weakly Supervised Learners for Correction of AI Errors with Provable Performance Guarantees
Feb 06, 2024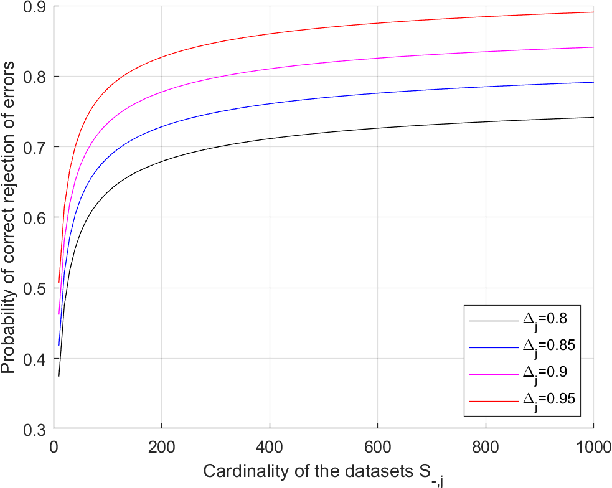

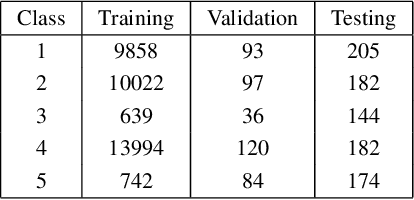
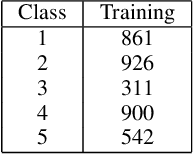
Abstract:We present a new methodology for handling AI errors by introducing weakly supervised AI error correctors with a priori performance guarantees. These AI correctors are auxiliary maps whose role is to moderate the decisions of some previously constructed underlying classifier by either approving or rejecting its decisions. The rejection of a decision can be used as a signal to suggest abstaining from making a decision. A key technical focus of the work is in providing performance guarantees for these new AI correctors through bounds on the probabilities of incorrect decisions. These bounds are distribution agnostic and do not rely on assumptions on the data dimension. Our empirical example illustrates how the framework can be applied to improve the performance of an image classifier in a challenging real-world task where training data are scarce.
The Boundaries of Verifiable Accuracy, Robustness, and Generalisation in Deep Learning
Sep 13, 2023Abstract:In this work, we assess the theoretical limitations of determining guaranteed stability and accuracy of neural networks in classification tasks. We consider classical distribution-agnostic framework and algorithms minimising empirical risks and potentially subjected to some weights regularisation. We show that there is a large family of tasks for which computing and verifying ideal stable and accurate neural networks in the above settings is extremely challenging, if at all possible, even when such ideal solutions exist within the given class of neural architectures.
How adversarial attacks can disrupt seemingly stable accurate classifiers
Sep 07, 2023



Abstract:Adversarial attacks dramatically change the output of an otherwise accurate learning system using a seemingly inconsequential modification to a piece of input data. Paradoxically, empirical evidence indicates that even systems which are robust to large random perturbations of the input data remain susceptible to small, easily constructed, adversarial perturbations of their inputs. Here, we show that this may be seen as a fundamental feature of classifiers working with high dimensional input data. We introduce a simple generic and generalisable framework for which key behaviours observed in practical systems arise with high probability -- notably the simultaneous susceptibility of the (otherwise accurate) model to easily constructed adversarial attacks, and robustness to random perturbations of the input data. We confirm that the same phenomena are directly observed in practical neural networks trained on standard image classification problems, where even large additive random noise fails to trigger the adversarial instability of the network. A surprising takeaway is that even small margins separating a classifier's decision surface from training and testing data can hide adversarial susceptibility from being detected using randomly sampled perturbations. Counterintuitively, using additive noise during training or testing is therefore inefficient for eradicating or detecting adversarial examples, and more demanding adversarial training is required.
Quasi-orthogonality and intrinsic dimensions as measures of learning and generalisation
Mar 30, 2022



Abstract:Finding best architectures of learning machines, such as deep neural networks, is a well-known technical and theoretical challenge. Recent work by Mellor et al (2021) showed that there may exist correlations between the accuracies of trained networks and the values of some easily computable measures defined on randomly initialised networks which may enable to search tens of thousands of neural architectures without training. Mellor et al used the Hamming distance evaluated over all ReLU neurons as such a measure. Motivated by these findings, in our work, we ask the question of the existence of other and perhaps more principled measures which could be used as determinants of success of a given neural architecture. In particular, we examine, if the dimensionality and quasi-orthogonality of neural networks' feature space could be correlated with the network's performance after training. We showed, using the setup as in Mellor et al, that dimensionality and quasi-orthogonality may jointly serve as network's performance discriminants. In addition to offering new opportunities to accelerate neural architecture search, our findings suggest important relationships between the networks' final performance and properties of their randomly initialised feature spaces: data dimension and quasi-orthogonality.
Demystification of Few-shot and One-shot Learning
Apr 25, 2021

Abstract:Few-shot and one-shot learning have been the subject of active and intensive research in recent years, with mounting evidence pointing to successful implementation and exploitation of few-shot learning algorithms in practice. Classical statistical learning theories do not fully explain why few- or one-shot learning is at all possible since traditional generalisation bounds normally require large training and testing samples to be meaningful. This sharply contrasts with numerous examples of successful one- and few-shot learning systems and applications. In this work we present mathematical foundations for a theory of one-shot and few-shot learning and reveal conditions specifying when such learning schemes are likely to succeed. Our theory is based on intrinsic properties of high-dimensional spaces. We show that if the ambient or latent decision space of a learning machine is sufficiently high-dimensional than a large class of objects in this space can indeed be easily learned from few examples provided that certain data non-concentration conditions are met.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge