Exploring the impact of social stress on the adaptive dynamics of COVID-19: Typing the behavior of naïve populations faced with epidemics

In the context of natural disasters, human responses inevitably intertwine with natural factors. The COVID-19 pandemic, as a significant stress factor, has brought to light profound variations among different countries in terms of their adaptive dynamics in addressing the spread of infection outbreaks across different regions. This emphasizes the crucial role of cultural characteristics in natural disaster analysis. The theoretical understanding of large-scale epidemics primarily relies on mean-field kinetic models. However, conventional SIR-like models failed to fully explain the observed phenomena at the onset of the COVID-19 outbreak. These phenomena included the unexpected cessation of exponential growth, the reaching of plateaus, and the occurrence of multi-wave dynamics. In situations where an outbreak of a highly virulent and unfamiliar infection arises, it becomes crucial to respond swiftly at a non-medical level to mitigate the negative socio-economic impact. Here we present a theoretical examination of the first wave of the epidemic based on a simple SIRSS model (SIR with Social Stress). We conduct an analysis of the socio-cultural features of na\"ive population behaviors across various countries worldwide. The unique characteristics of each country/territory are encapsulated in only a few constants within our model, derived from the fitted COVID-19 statistics. These constants also reflect the societal response dynamics to the external stress factor, underscoring the importance of studying the mutual behavior of humanity and natural factors during global social disasters. Based on these distinctive characteristics of specific regions, local authorities can optimize their strategies to effectively combat epidemics until vaccines are developed.

Domain Adaptation Principal Component Analysis: base linear method for learning with out-of-distribution data

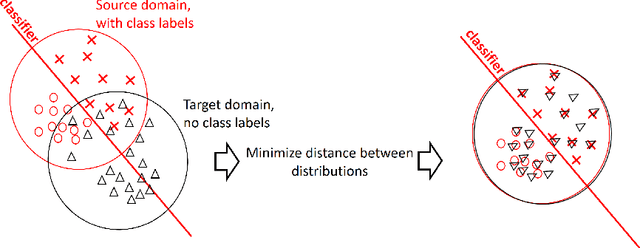
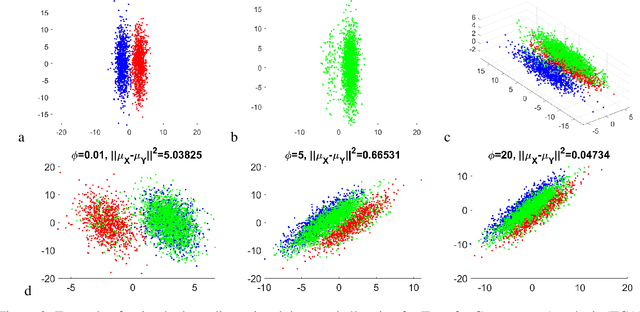
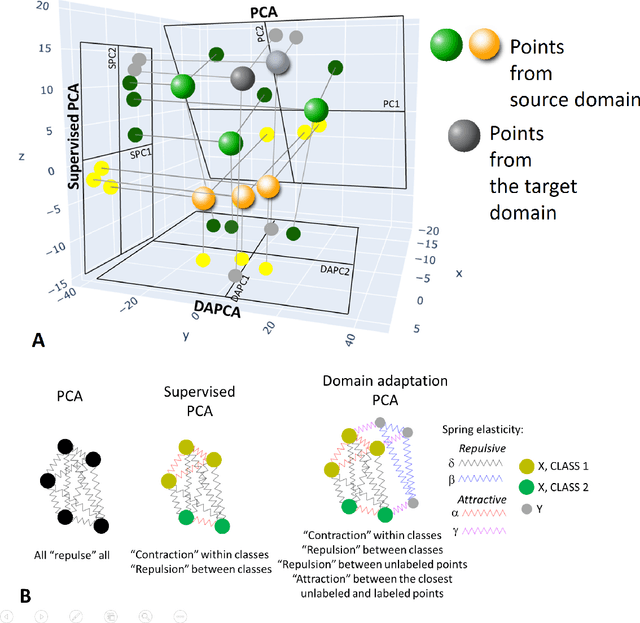
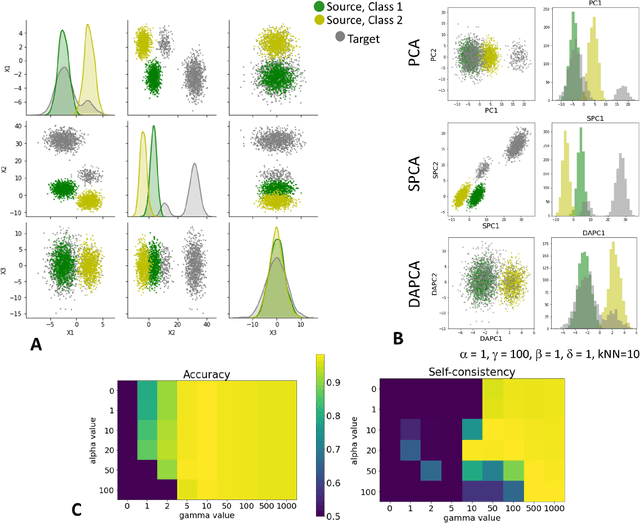
Domain adaptation is a popular paradigm in modern machine learning which aims at tackling the problem of divergence between training or validation dataset possessing labels for learning and testing a classifier (source domain) and a potentially large unlabeled dataset where the model is exploited (target domain). The task is to find such a common representation of both source and target datasets in which the source dataset is informative for training and such that the divergence between source and target would be minimized. Most popular solutions for domain adaptation are currently based on training neural networks that combine classification and adversarial learning modules, which are data hungry and usually difficult to train. We present a method called Domain Adaptation Principal Component Analysis (DAPCA) which finds a linear reduced data representation useful for solving the domain adaptation task. DAPCA is based on introducing positive and negative weights between pairs of data points and generalizes the supervised extension of principal component analysis. DAPCA represents an iterative algorithm such that at each iteration a simple quadratic optimization problem is solved. The convergence of the algorithm is guaranteed and the number of iterations is small in practice. We validate the suggested algorithm on previously proposed benchmarks for solving the domain adaptation task, and also show the benefit of using DAPCA in the analysis of single cell omics datasets in biomedical applications. Overall, DAPCA can serve as a useful preprocessing step in many machine learning applications leading to reduced dataset representations, taking into account possible divergence between source and target domains.

Quasi-orthogonality and intrinsic dimensions as measures of learning and generalisation

Finding best architectures of learning machines, such as deep neural networks, is a well-known technical and theoretical challenge. Recent work by Mellor et al (2021) showed that there may exist correlations between the accuracies of trained networks and the values of some easily computable measures defined on randomly initialised networks which may enable to search tens of thousands of neural architectures without training. Mellor et al used the Hamming distance evaluated over all ReLU neurons as such a measure. Motivated by these findings, in our work, we ask the question of the existence of other and perhaps more principled measures which could be used as determinants of success of a given neural architecture. In particular, we examine, if the dimensionality and quasi-orthogonality of neural networks' feature space could be correlated with the network's performance after training. We showed, using the setup as in Mellor et al, that dimensionality and quasi-orthogonality may jointly serve as network's performance discriminants. In addition to offering new opportunities to accelerate neural architecture search, our findings suggest important relationships between the networks' final performance and properties of their randomly initialised feature spaces: data dimension and quasi-orthogonality.

Scikit-dimension: a Python package for intrinsic dimension estimation

Dealing with uncertainty in applications of machine learning to real-life data critically depends on the knowledge of intrinsic dimensionality (ID). A number of methods have been suggested for the purpose of estimating ID, but no standard package to easily apply them one by one or all at once has been implemented in Python. This technical note introduces \texttt{scikit-dimension}, an open-source Python package for intrinsic dimension estimation. \texttt{scikit-dimension} package provides a uniform implementation of most of the known ID estimators based on scikit-learn application programming interface to evaluate global and local intrinsic dimension, as well as generators of synthetic toy and benchmark datasets widespread in the literature. The package is developed with tools assessing the code quality, coverage, unit testing and continuous integration. We briefly describe the package and demonstrate its use in a large-scale (more than 500 datasets) benchmarking of methods for ID estimation in real-life and synthetic data. The source code is available from https://github.com/j-bac/scikit-dimension , the documentation is available from https://scikit-dimension.readthedocs.io .

Trajectories, bifurcations and pseudotime in large clinical datasets: applications to myocardial infarction and diabetes data

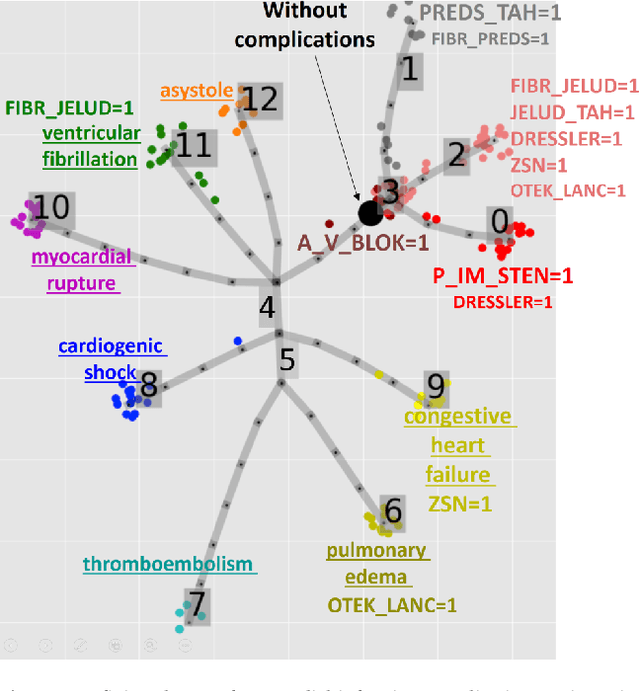
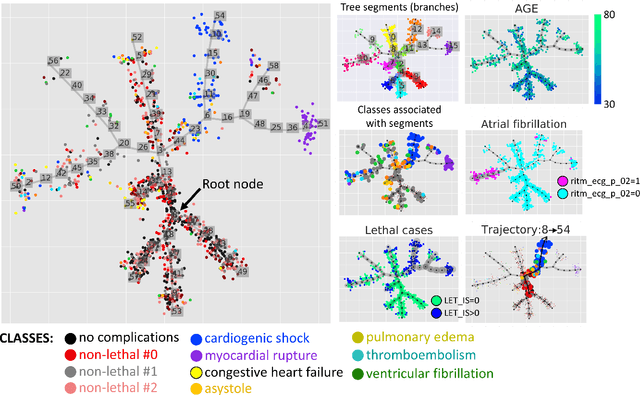
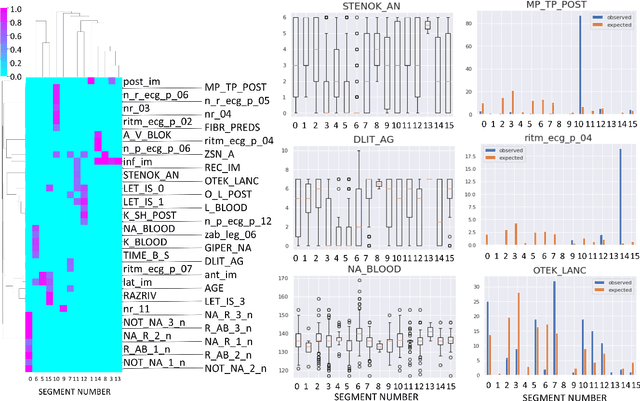
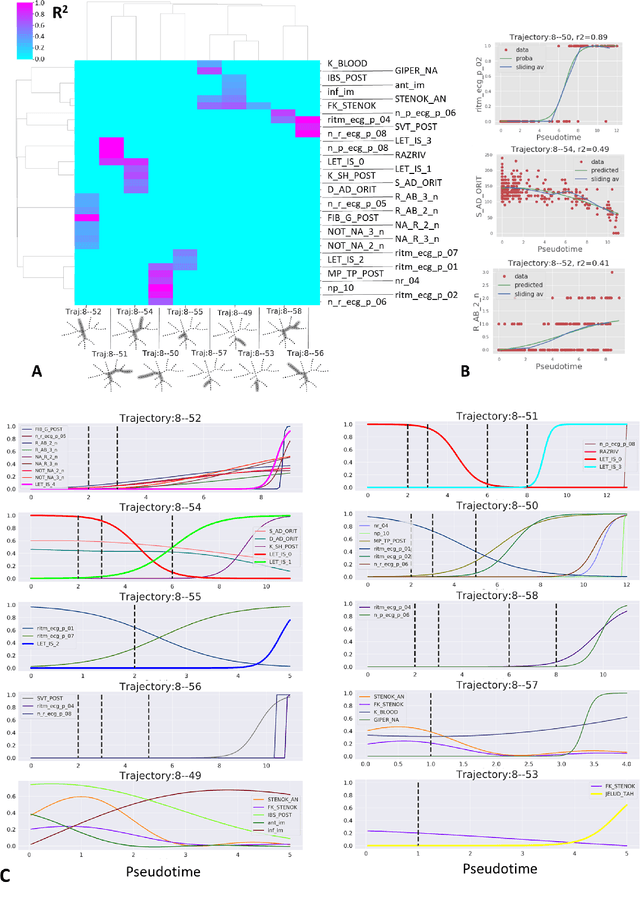
Large observational clinical datasets become increasingly available for mining associations between various disease traits and administered therapy. These datasets can be considered as representations of the landscape of all possible disease conditions, in which a concrete pathology develops through a number of stereotypical routes, characterized by `points of no return' and `final states' (such as lethal or recovery states). Extracting this information directly from the data remains challenging, especially in the case of synchronic (with a short-term follow up) observations. Here we suggest a semi-supervised methodology for the analysis of large clinical datasets, characterized by mixed data types and missing values, through modeling the geometrical data structure as a bouquet of bifurcating clinical trajectories. The methodology is based on application of elastic principal graphs which can address simultaneously the tasks of dimensionality reduction, data visualization, clustering, feature selection and quantifying the geodesic distances (pseudotime) in partially ordered sequences of observations. The methodology allows positioning a patient on a particular clinical trajectory (pathological scenario) and characterizing the degree of progression along it with a qualitative estimate of the uncertainty of the prognosis. Overall, our pseudo-time quantification-based approach gives a possibility to apply the methods developed for dynamical disease phenotyping and illness trajectory analysis (diachronic data analysis) to synchronic observational data. We developed a tool $ClinTrajan$ for clinical trajectory analysis implemented in Python programming language. We test the methodology in two large publicly available datasets: myocardial infarction complications and readmission of diabetic patients data.

Local intrinsic dimensionality estimators based on concentration of measure

Intrinsic dimensionality (ID) is one of the most fundamental characteristics of multi-dimensional data point clouds. Knowing ID is crucial to choose the appropriate machine learning approach as well as to understand its behavior and validate it. ID can be computed globally for the whole data distribution, or computed locally in different regions of the dataset. In this paper, we introduce new local estimators of ID based on linear separability of multi-dimensional data point clouds, which is one of the manifestations of concentration of measure. We empirically study the properties of these estimators and compare them with other recently introduced ID estimators exploiting various effects of measure concentration. Observed differences between estimators can be used to anticipate their behaviour in practical applications.

Synthesis of Boolean Networks from Biological Dynamical Constraints using Answer-Set Programming

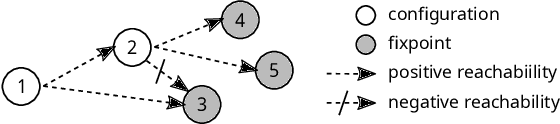
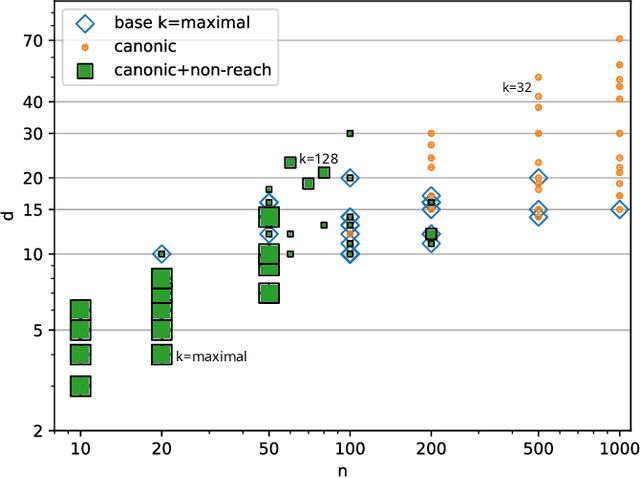
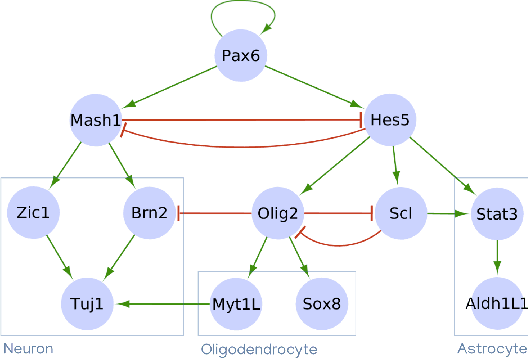
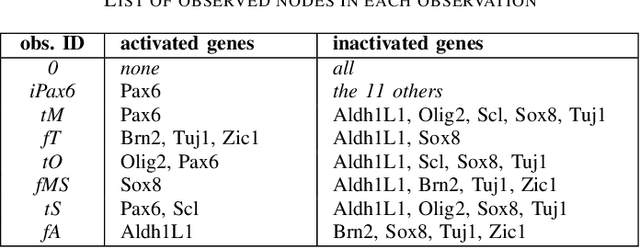
Boolean networks model finite discrete dynamical systems with complex behaviours. The state of each component is determined by a Boolean function of the state of (a subset of) the components of the network. This paper addresses the synthesis of these Boolean functions from constraints on their domain and emerging dynamical properties of the resulting network. The dynamical properties relate to the existence and absence of trajectories between partially observed configurations, and to the stable behaviours (fixpoints and cyclic attractors). The synthesis is expressed as a Boolean satisfiability problem relying on Answer-Set Programming with a parametrized complexity, and leads to a complete non-redundant characterization of the set of solutions. Considered constraints are particularly suited to address the synthesis of models of cellular differentiation processes, as illustrated on a case study. The scalability of the approach is demonstrated on random networks with scale-free structures up to 100 to 1,000 nodes depending on the type of constraints.

Estimating the effective dimension of large biological datasets using Fisher separability analysis

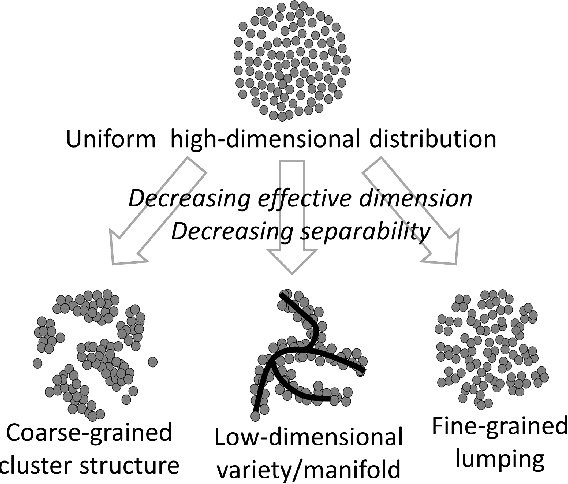
Modern large-scale datasets are frequently said to be high-dimensional. However, their data point clouds frequently possess structures, significantly decreasing their intrinsic dimensionality (ID) due to the presence of clusters, points being located close to low-dimensional varieties or fine-grained lumping. We test a recently introduced dimensionality estimator, based on analysing the separability properties of data points, on several benchmarks and real biological datasets. We show that the introduced measure of ID has performance competitive with state-of-the-art measures, being efficient across a wide range of dimensions and performing better in the case of noisy samples. Moreover, it allows estimating the intrinsic dimension in situations where the intrinsic manifold assumption is not valid.

Robust And Scalable Learning Of Complex Dataset Topologies Via Elpigraph

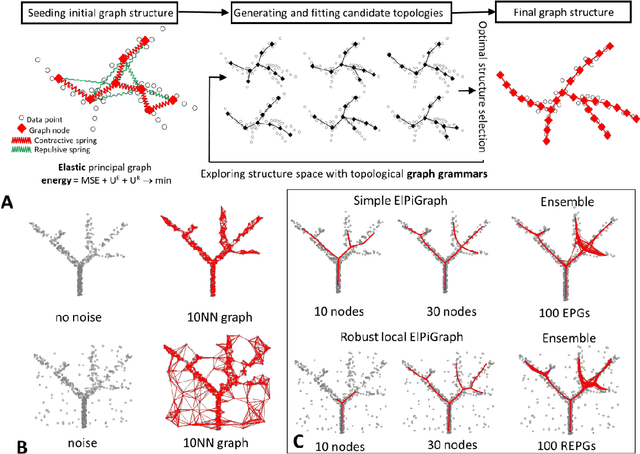
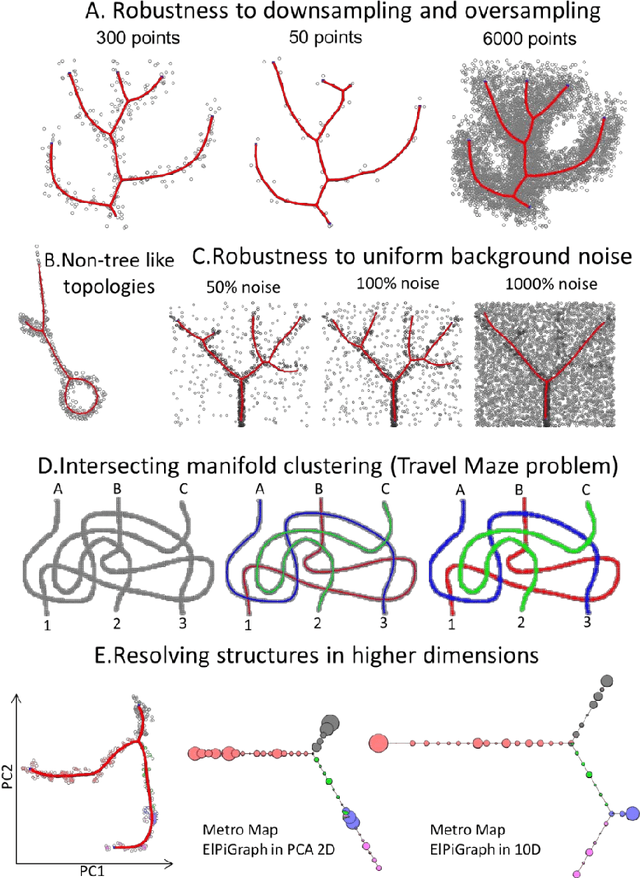
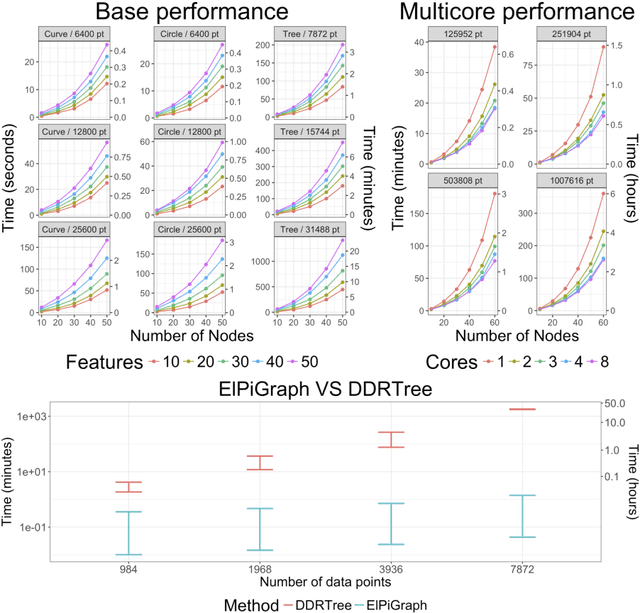
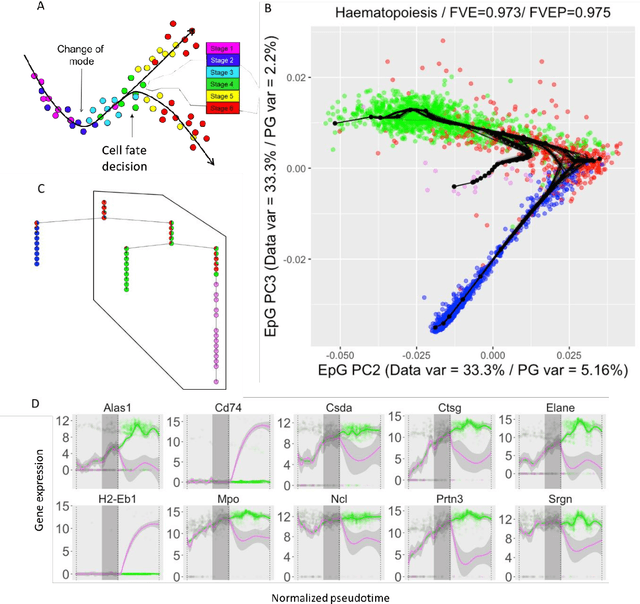
Large datasets represented by multidimensional data point clouds often possess non-trivial distributions with branching trajectories and excluded regions, with the recent single-cell transcriptomic studies of developing embryo being notable examples. Reducing the complexity and producing compact and interpretable representations of such data remains a challenging task. Most of the existing computational methods are based on exploring the local data point neighbourhood relations, a step that can perform poorly in the case of multidimensional and noisy data. Here we present ElPiGraph, a scalable and robust method for approximation of datasets with complex structures which does not require computing the complete data distance matrix or the data point neighbourhood graph. This method is able to withstand high levels of noise and is capable of approximating complex topologies via principal graph ensembles that can be combined into a consensus principal graph. ElPiGraph deals efficiently with large and complex datasets in various fields from biology, where it can be used to infer gene dynamics from single-cell RNA-Seq, to astronomy, where it can be used to explore complex structures in the distribution of galaxies.

Data complexity measured by principal graphs

How to measure the complexity of a finite set of vectors embedded in a multidimensional space? This is a non-trivial question which can be approached in many different ways. Here we suggest a set of data complexity measures using universal approximators, principal cubic complexes. Principal cubic complexes generalise the notion of principal manifolds for datasets with non-trivial topologies. The type of the principal cubic complex is determined by its dimension and a grammar of elementary graph transformations. The simplest grammar produces principal trees. We introduce three natural types of data complexity: 1) geometric (deviation of the data's approximator from some "idealized" configuration, such as deviation from harmonicity); 2) structural (how many elements of a principal graph are needed to approximate the data), and 3) construction complexity (how many applications of elementary graph transformations are needed to construct the principal object starting from the simplest one). We compute these measures for several simulated and real-life data distributions and show them in the "accuracy-complexity" plots, helping to optimize the accuracy/complexity ratio. We discuss various issues connected with measuring data complexity. Software for computing data complexity measures from principal cubic complexes is provided as well.