Tackling Universal Properties of Minimal Trap Spaces of Boolean Networks

Minimal trap spaces (MTSs) capture subspaces in which the Boolean dynamics is trapped, whatever the update mode. They correspond to the attractors of the most permissive mode. Due to their versatility, the computation of MTSs has recently gained traction, essentially by focusing on their enumeration. In this paper, we address the logical reasoning on universal properties of MTSs in the scope of two problems: the reprogramming of Boolean networks for identifying the permanent freeze of Boolean variables that enforce a given property on all the MTSs, and the synthesis of Boolean networks from universal properties on their MTSs. Both problems reduce to solving the satisfiability of quantified propositional logic formula with 3 levels of quantifiers ($\exists\forall\exists$). In this paper, we introduce a Counter-Example Guided Refinement Abstraction (CEGAR) to efficiently solve these problems by coupling the resolution of two simpler formulas. We provide a prototype relying on Answer-Set Programming for each formula and show its tractability on a wide range of Boolean models of biological networks.

Marker and source-marker reprogramming of Most Permissive Boolean networks and ensembles with BoNesis

Boolean networks (BNs) are discrete dynamical systems with applications to the modeling of cellular behaviors. In this paper, we demonstrate how the software BoNesis can be employed to exhaustively identify combinations of perturbations which enforce properties on their fixed points and attractors. We consider marker properties, which specify that some components are fixed to a specific value. We study 4 variants of the marker reprogramming problem: the reprogramming of fixed points, of minimal trap spaces, and of fixed points and minimal trap spaces reachable from a given initial configuration with the most permissive update mode. The perturbations consist of fixing a set of components to a fixed value. They can destroy and create new attractors. In each case, we give an upper bound on their theoretical computational complexity, and give an implementation of the resolution using the BoNesis Python framework. Finally, we lift the reprogramming problems to ensembles of BNs, as supported by BoNesis, bringing insight on possible and universal reprogramming strategies. This paper can be executed and modified interactively.

SAT Heritage: a community-driven effort for archiving, building and running more than thousand SAT solvers

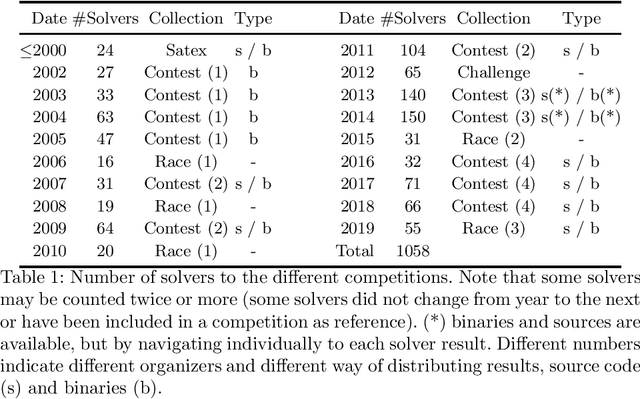
SAT research has a long history of source code and binary releases, thanks to competitions organized every year. However, since every cycle of competitions has its own set of rules and an adhoc way of publishing source code and binaries, compiling or even running any solver may be harder than what it seems. Moreover, there has been more than a thousand solvers published so far, some of them released in the early 90's. If the SAT community wants to archive and be able to keep track of all the solvers that made its history, it urgently needs to deploy an important effort. We propose to initiate a community-driven effort to archive and to allow easy compilation and running of all SAT solvers that have been released so far. We rely on the best tools for archiving and building binaries (thanks to Docker, GitHub and Zenodo) and provide a consistent and easy way for this. Thanks to our tool, building (or running) a solver from its source (or from its binary) can be done in one line.

Synthesis of Boolean Networks from Biological Dynamical Constraints using Answer-Set Programming

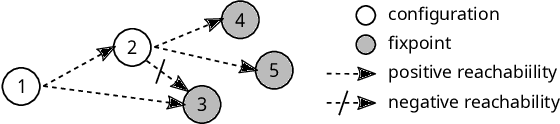
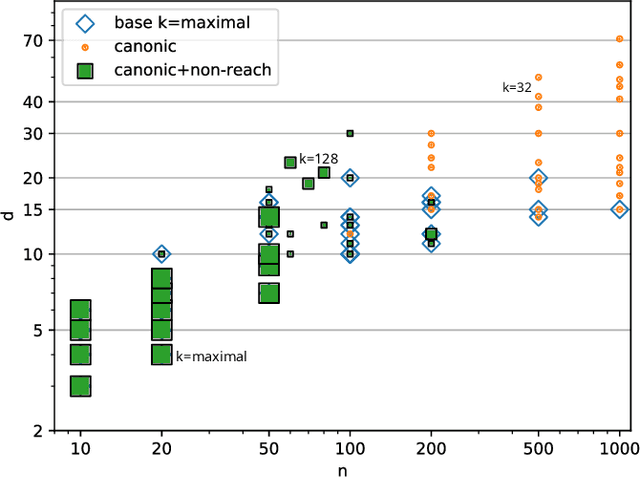
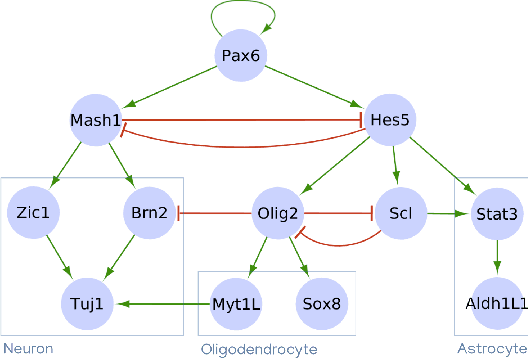
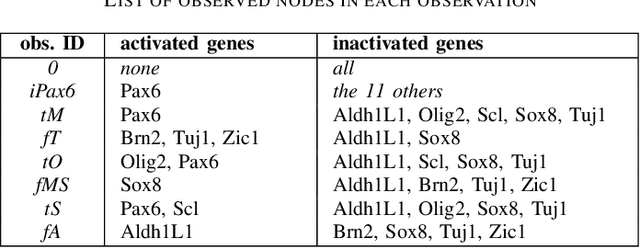
Boolean networks model finite discrete dynamical systems with complex behaviours. The state of each component is determined by a Boolean function of the state of (a subset of) the components of the network. This paper addresses the synthesis of these Boolean functions from constraints on their domain and emerging dynamical properties of the resulting network. The dynamical properties relate to the existence and absence of trajectories between partially observed configurations, and to the stable behaviours (fixpoints and cyclic attractors). The synthesis is expressed as a Boolean satisfiability problem relying on Answer-Set Programming with a parametrized complexity, and leads to a complete non-redundant characterization of the set of solutions. Considered constraints are particularly suited to address the synthesis of models of cellular differentiation processes, as illustrated on a case study. The scalability of the approach is demonstrated on random networks with scale-free structures up to 100 to 1,000 nodes depending on the type of constraints.