Proceedings of the 2024 XCSP3 Competition

This document represents the proceedings of the 2024 XCSP3 Competition. The results of this competition of constraint solvers were presented at CP'24 (30th International Conference on Principles and Practice of Constraint Programming).

Proceedings of the 2023 XCSP3 Competition

This document represents the proceedings of the 2023 XCSP3 Competition. The results of this competition of constraint solvers were presented at CP'23 (the 29th International Conference on Principles and Practice of Constraint Programming, held in Toronto, Canada from 27th to 31th August, 2023).

Computing Abductive Explanations for Boosted Trees

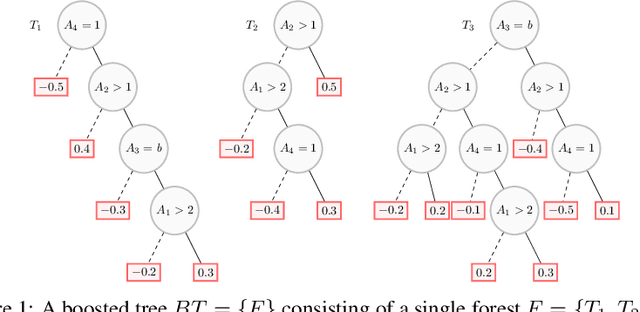
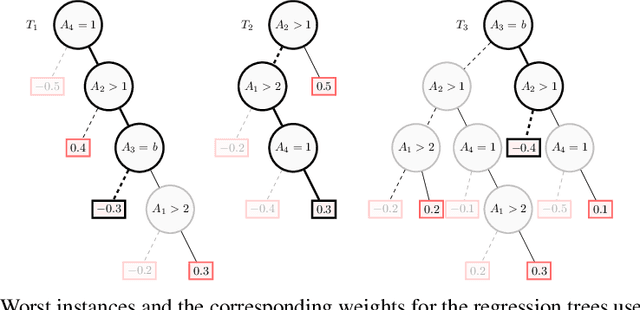
Boosted trees is a dominant ML model, exhibiting high accuracy. However, boosted trees are hardly intelligible, and this is a problem whenever they are used in safety-critical applications. Indeed, in such a context, rigorous explanations of the predictions made are expected. Recent work have shown how subset-minimal abductive explanations can be derived for boosted trees, using automated reasoning techniques. However, the generation of such well-founded explanations is intractable in the general case. To improve the scalability of their generation, we introduce the notion of tree-specific explanation for a boosted tree. We show that tree-specific explanations are abductive explanations that can be computed in polynomial time. We also explain how to derive a subset-minimal abductive explanation from a tree-specific explanation. Experiments on various datasets show the computational benefits of leveraging tree-specific explanations for deriving subset-minimal abductive explanations.

Proceedings of the 2022 XCSP3 Competition

This document represents the proceedings of the 2022 XCSP3 Competition. The results of this competition of constraint solvers were presented at FLOC (Federated Logic Conference) 2022 Olympic Games, held in Haifa, Israel from 31th July 2022 to 7th August, 2022.

On the Explanatory Power of Decision Trees

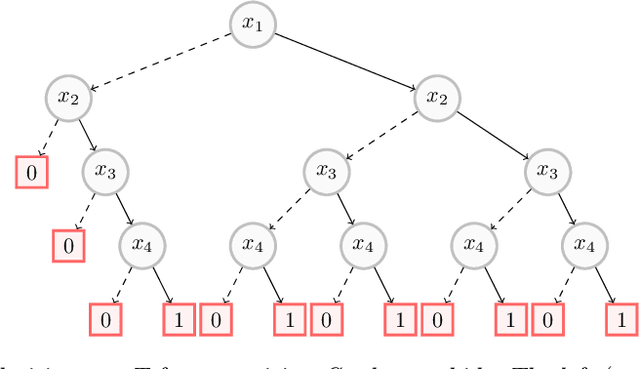
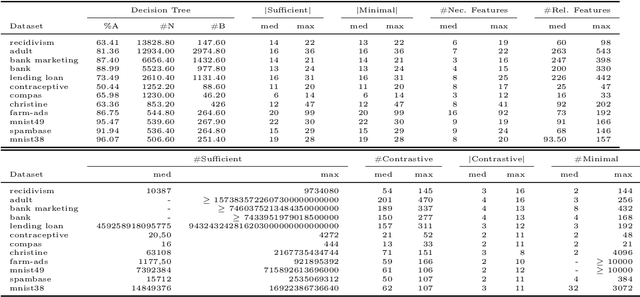
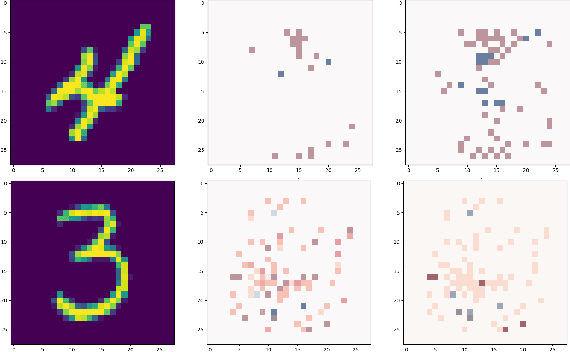
Decision trees have long been recognized as models of choice in sensitive applications where interpretability is of paramount importance. In this paper, we examine the computational ability of Boolean decision trees in deriving, minimizing, and counting sufficient reasons and contrastive explanations. We prove that the set of all sufficient reasons of minimal size for an instance given a decision tree can be exponentially larger than the size of the input (the instance and the decision tree). Therefore, generating the full set of sufficient reasons can be out of reach. In addition, computing a single sufficient reason does not prove enough in general; indeed, two sufficient reasons for the same instance may differ on many features. To deal with this issue and generate synthetic views of the set of all sufficient reasons, we introduce the notions of relevant features and of necessary features that characterize the (possibly negated) features appearing in at least one or in every sufficient reason, and we show that they can be computed in polynomial time. We also introduce the notion of explanatory importance, that indicates how frequent each (possibly negated) feature is in the set of all sufficient reasons. We show how the explanatory importance of a feature and the number of sufficient reasons can be obtained via a model counting operation, which turns out to be practical in many cases. We also explain how to enumerate sufficient reasons of minimal size. We finally show that, unlike sufficient reasons, the set of all contrastive explanations for an instance given a decision tree can be derived, minimized and counted in polynomial time.

Trading Complexity for Sparsity in Random Forest Explanations

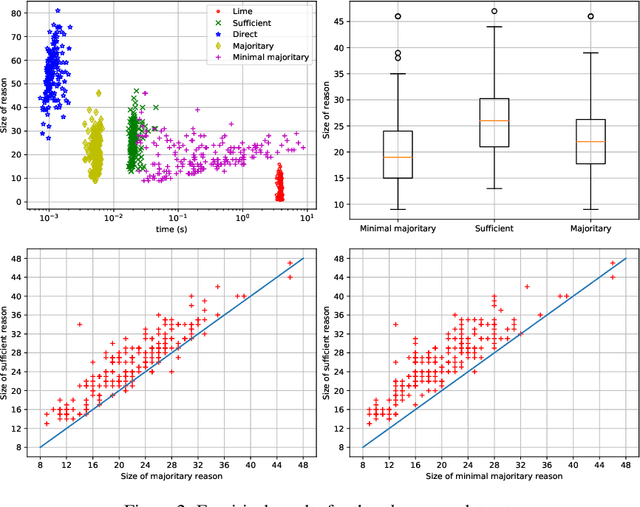
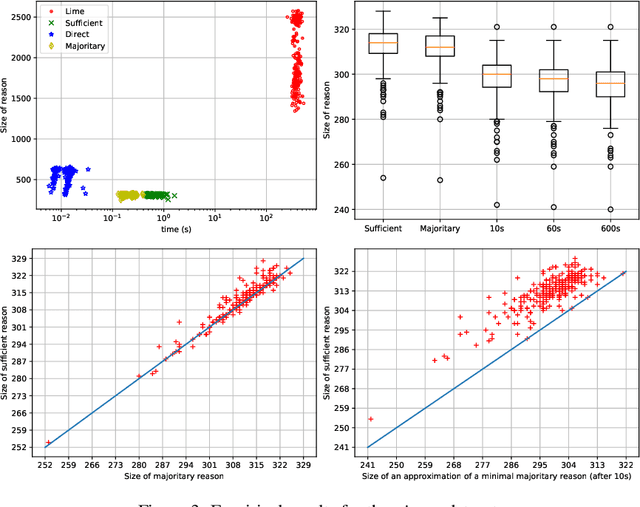
Random forests have long been considered as powerful model ensembles in machine learning. By training multiple decision trees, whose diversity is fostered through data and feature subsampling, the resulting random forest can lead to more stable and reliable predictions than a single decision tree. This however comes at the cost of decreased interpretability: while decision trees are often easily interpretable, the predictions made by random forests are much more difficult to understand, as they involve a majority vote over hundreds of decision trees. In this paper, we examine different types of reasons that explain "why" an input instance is classified as positive or negative by a Boolean random forest. Notably, as an alternative to sufficient reasons taking the form of prime implicants of the random forest, we introduce majoritary reasons which are prime implicants of a strict majority of decision trees. For these different abductive explanations, the tractability of the generation problem (finding one reason) and the minimization problem (finding one shortest reason) are investigated. Experiments conducted on various datasets reveal the existence of a trade-off between runtime complexity and sparsity. Sufficient reasons - for which the identification problem is DP-complete - are slightly larger than majoritary reasons that can be generated using a simple linear- time greedy algorithm, and significantly larger than minimal majoritary reasons that can be approached using an anytime P ARTIAL M AX SAT algorithm.

On the Computational Intelligibility of Boolean Classifiers

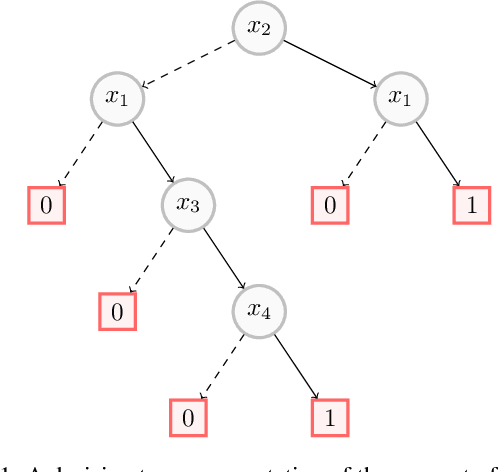
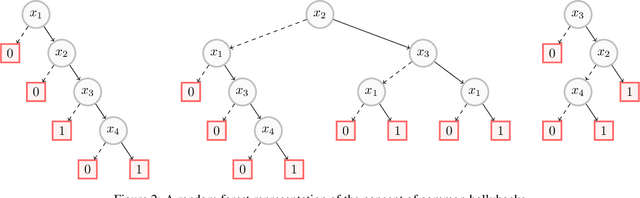
In this paper, we investigate the computational intelligibility of Boolean classifiers, characterized by their ability to answer XAI queries in polynomial time. The classifiers under consideration are decision trees, DNF formulae, decision lists, decision rules, tree ensembles, and Boolean neural nets. Using 9 XAI queries, including both explanation queries and verification queries, we show the existence of large intelligibility gap between the families of classifiers. On the one hand, all the 9 XAI queries are tractable for decision trees. On the other hand, none of them is tractable for DNF formulae, decision lists, random forests, boosted decision trees, Boolean multilayer perceptrons, and binarized neural networks.

XCSP3-core: A Format for Representing Constraint Satisfaction/Optimization Problems

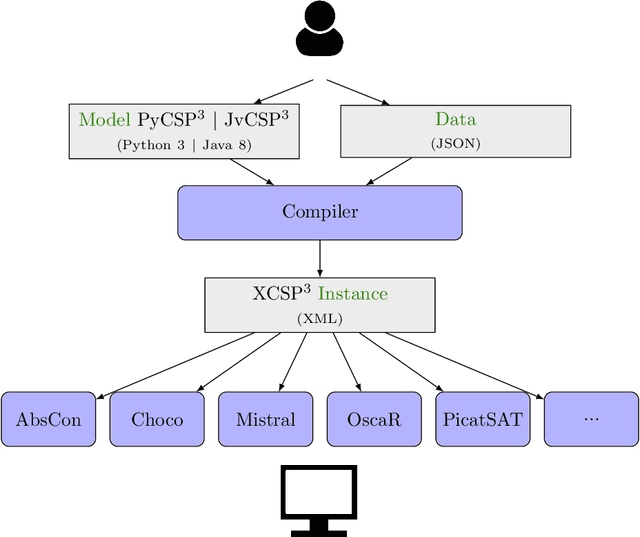
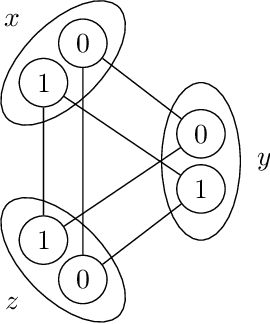
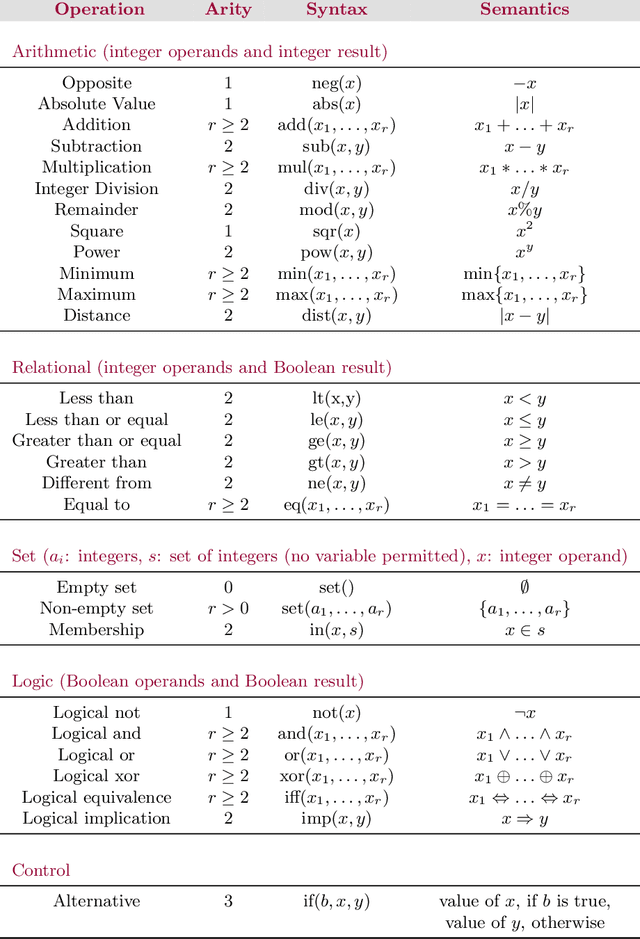
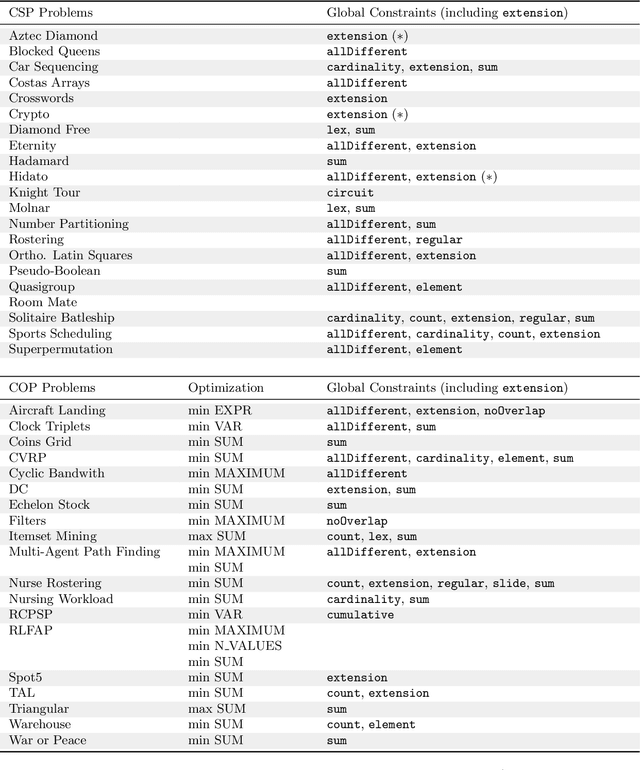
In this document, we introduce XCSP3-core, a subset of XCSP3 that allows us to represent constraint satisfaction/optimization problems. The interest of XCSP3-core is multiple: (i) focusing on the most popular frameworks (CSP and COP) and constraints, (ii) facilitating the parsing process by means of dedicated XCSP3-core parsers written in Java and C++ (using callback functions), (iii) and defining a core format for comparisons (competitions) of constraint solvers.

SAT Heritage: a community-driven effort for archiving, building and running more than thousand SAT solvers

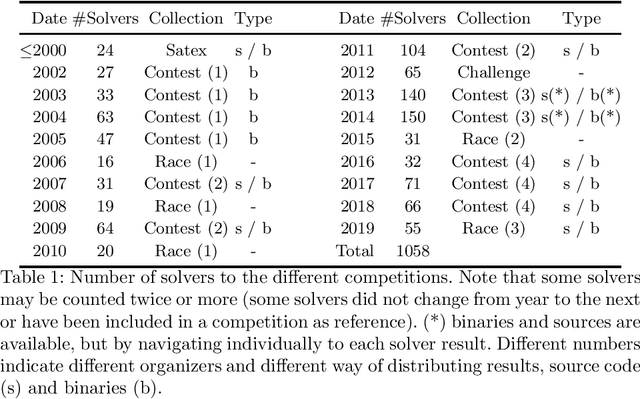
SAT research has a long history of source code and binary releases, thanks to competitions organized every year. However, since every cycle of competitions has its own set of rules and an adhoc way of publishing source code and binaries, compiling or even running any solver may be harder than what it seems. Moreover, there has been more than a thousand solvers published so far, some of them released in the early 90's. If the SAT community wants to archive and be able to keep track of all the solvers that made its history, it urgently needs to deploy an important effort. We propose to initiate a community-driven effort to archive and to allow easy compilation and running of all SAT solvers that have been released so far. We rely on the best tools for archiving and building binaries (thanks to Docker, GitHub and Zenodo) and provide a consistent and easy way for this. Thanks to our tool, building (or running) a solver from its source (or from its binary) can be done in one line.

XCSP3: An Integrated Format for Benchmarking Combinatorial Constrained Problems

We propose a major revision of the format XCSP 2.1, called XCSP3, to build integrated representations of combinatorial constrained problems. This new format is able to deal with mono/multi optimization, many types of variables, cost functions, reification, views, annotations, variable quantification, distributed, probabilistic and qualitative reasoning. The new format is made compact, highly readable, and rather easy to parse. Interestingly, it captures the structure of the problem models, through the possibilities of declaring arrays of variables, and identifying syntactic and semantic groups of constraints. The number of constraints is kept under control by introducing a limited set of basic constraint forms, and producing almost automatically some of their variations through lifting, restriction, sliding, logical combination and relaxation mechanisms. As a result, XCSP3 encompasses practically all constraints that can be found in major constraint solvers developed by the CP community. A website, which is developed conjointly with the format, contains many models and series of instances. The user can make sophisticated queries for selecting instances from very precise criteria. The objective of XCSP3 is to ease the effort required to test and compare different algorithms by providing a common test-bed of combinatorial constrained instances.