Learning Model Agnostic Explanations via Constraint Programming

Interpretable Machine Learning faces a recurring challenge of explaining the predictions made by opaque classifiers such as ensemble models, kernel methods, or neural networks in terms that are understandable to humans. When the model is viewed as a black box, the objective is to identify a small set of features that jointly determine the black box response with minimal error. However, finding such model-agnostic explanations is computationally demanding, as the problem is intractable even for binary classifiers. In this paper, the task is framed as a Constraint Optimization Problem, where the constraint solver seeks an explanation of minimum error and bounded size for an input data instance and a set of samples generated by the black box. From a theoretical perspective, this constraint programming approach offers PAC-style guarantees for the output explanation. We evaluate the approach empirically on various datasets and show that it statistically outperforms the state-of-the-art heuristic Anchors method.

Dynamic Blocked Clause Elimination for Projected Model Counting

In this paper, we explore the application of blocked clause elimination for projected model counting. This is the problem of determining the number of models ||\exists X.{\Sigma}|| of a propositional formula {\Sigma} after eliminating a given set X of variables existentially. Although blocked clause elimination is a well-known technique for SAT solving, its direct application to model counting is challenging as in general it changes the number of models. However, we demonstrate, by focusing on projected variables during the blocked clause search, that blocked clause elimination can be leveraged while preserving the correct model count. To take advantage of blocked clause elimination in an efficient way during model counting, a novel data structure and associated algorithms are introduced. Our proposed approach is implemented in the model counter d4. Our experiments demonstrate the computational benefits of our new method of blocked clause elimination for projected model counting.

Tackling Universal Properties of Minimal Trap Spaces of Boolean Networks

Minimal trap spaces (MTSs) capture subspaces in which the Boolean dynamics is trapped, whatever the update mode. They correspond to the attractors of the most permissive mode. Due to their versatility, the computation of MTSs has recently gained traction, essentially by focusing on their enumeration. In this paper, we address the logical reasoning on universal properties of MTSs in the scope of two problems: the reprogramming of Boolean networks for identifying the permanent freeze of Boolean variables that enforce a given property on all the MTSs, and the synthesis of Boolean networks from universal properties on their MTSs. Both problems reduce to solving the satisfiability of quantified propositional logic formula with 3 levels of quantifiers ($\exists\forall\exists$). In this paper, we introduce a Counter-Example Guided Refinement Abstraction (CEGAR) to efficiently solve these problems by coupling the resolution of two simpler formulas. We provide a prototype relying on Answer-Set Programming for each formula and show its tractability on a wide range of Boolean models of biological networks.

Computing Abductive Explanations for Boosted Trees

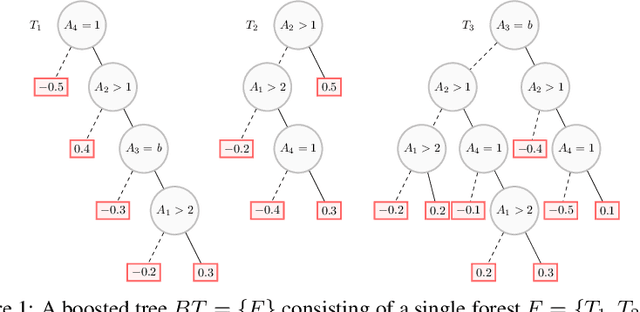
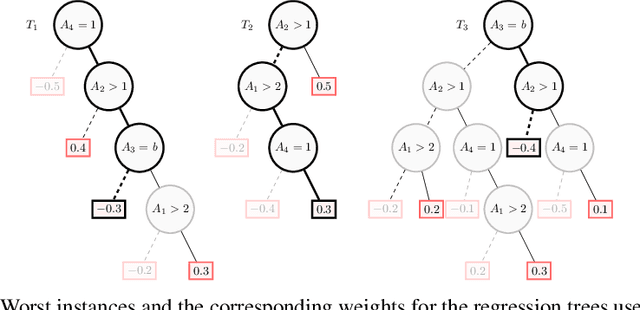
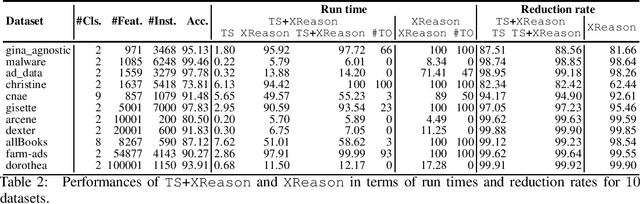
Boosted trees is a dominant ML model, exhibiting high accuracy. However, boosted trees are hardly intelligible, and this is a problem whenever they are used in safety-critical applications. Indeed, in such a context, rigorous explanations of the predictions made are expected. Recent work have shown how subset-minimal abductive explanations can be derived for boosted trees, using automated reasoning techniques. However, the generation of such well-founded explanations is intractable in the general case. To improve the scalability of their generation, we introduce the notion of tree-specific explanation for a boosted tree. We show that tree-specific explanations are abductive explanations that can be computed in polynomial time. We also explain how to derive a subset-minimal abductive explanation from a tree-specific explanation. Experiments on various datasets show the computational benefits of leveraging tree-specific explanations for deriving subset-minimal abductive explanations.

Design and Results of ICCMA 2021

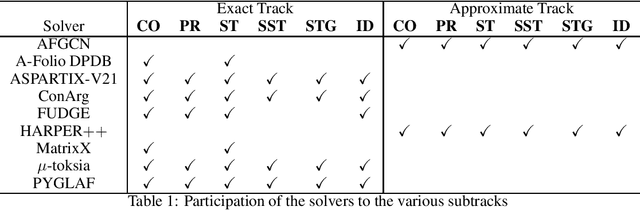
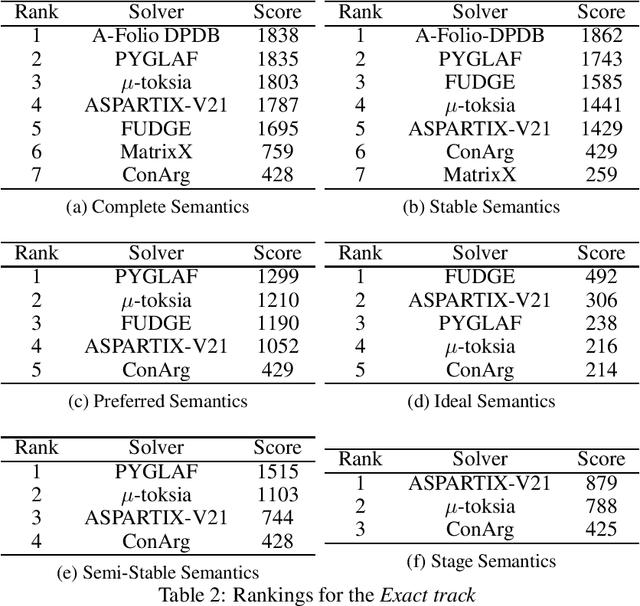
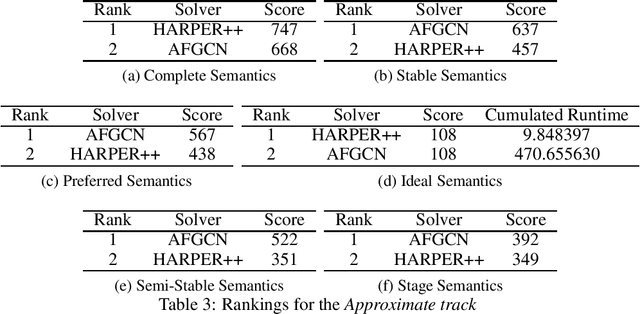
Since 2015, the International Competition on Computational Models of Argumentation (ICCMA) provides a systematic comparison of the different algorithms for solving some classical reasoning problems in the domain of abstract argumentation. This paper discusses the design of the Fourth International Competition on Computational Models of Argumentation. We describe the rules of the competition and the benchmark selection method that we used. After a brief presentation of the competitors, we give an overview of the results.

On the Explanatory Power of Decision Trees

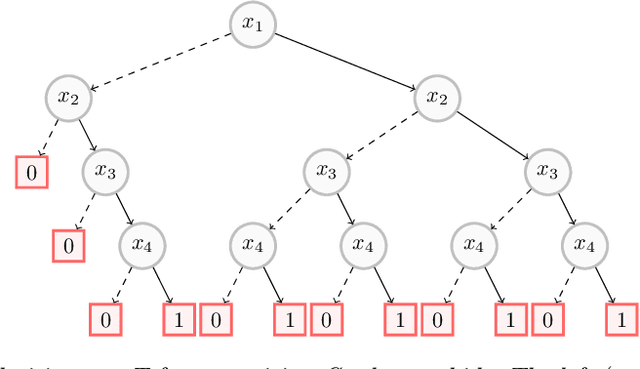
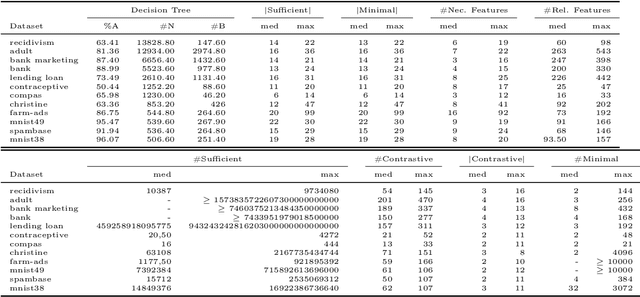
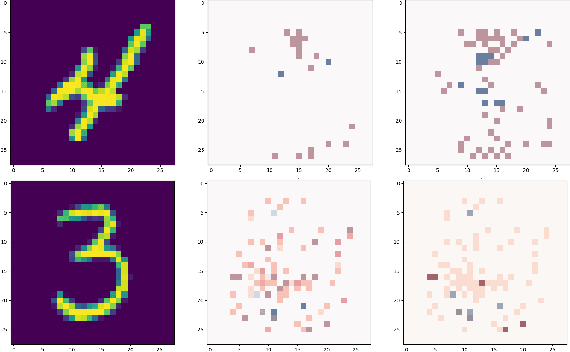
Decision trees have long been recognized as models of choice in sensitive applications where interpretability is of paramount importance. In this paper, we examine the computational ability of Boolean decision trees in deriving, minimizing, and counting sufficient reasons and contrastive explanations. We prove that the set of all sufficient reasons of minimal size for an instance given a decision tree can be exponentially larger than the size of the input (the instance and the decision tree). Therefore, generating the full set of sufficient reasons can be out of reach. In addition, computing a single sufficient reason does not prove enough in general; indeed, two sufficient reasons for the same instance may differ on many features. To deal with this issue and generate synthetic views of the set of all sufficient reasons, we introduce the notions of relevant features and of necessary features that characterize the (possibly negated) features appearing in at least one or in every sufficient reason, and we show that they can be computed in polynomial time. We also introduce the notion of explanatory importance, that indicates how frequent each (possibly negated) feature is in the set of all sufficient reasons. We show how the explanatory importance of a feature and the number of sufficient reasons can be obtained via a model counting operation, which turns out to be practical in many cases. We also explain how to enumerate sufficient reasons of minimal size. We finally show that, unlike sufficient reasons, the set of all contrastive explanations for an instance given a decision tree can be derived, minimized and counted in polynomial time.

Trading Complexity for Sparsity in Random Forest Explanations

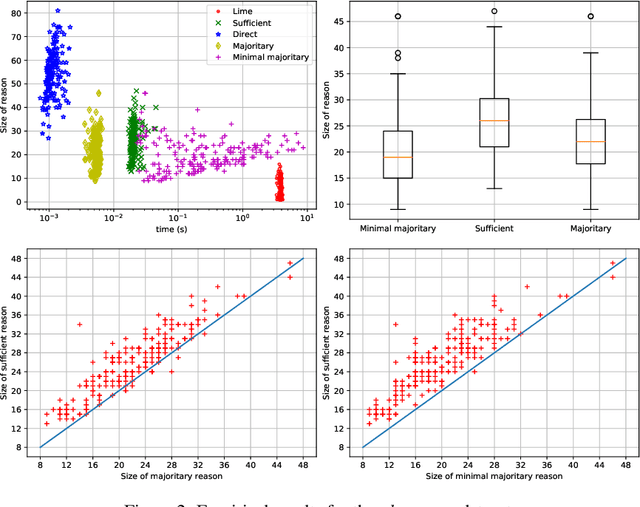
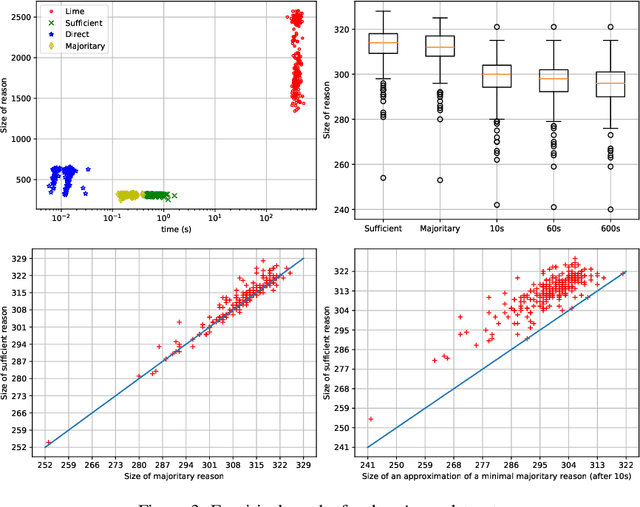
Random forests have long been considered as powerful model ensembles in machine learning. By training multiple decision trees, whose diversity is fostered through data and feature subsampling, the resulting random forest can lead to more stable and reliable predictions than a single decision tree. This however comes at the cost of decreased interpretability: while decision trees are often easily interpretable, the predictions made by random forests are much more difficult to understand, as they involve a majority vote over hundreds of decision trees. In this paper, we examine different types of reasons that explain "why" an input instance is classified as positive or negative by a Boolean random forest. Notably, as an alternative to sufficient reasons taking the form of prime implicants of the random forest, we introduce majoritary reasons which are prime implicants of a strict majority of decision trees. For these different abductive explanations, the tractability of the generation problem (finding one reason) and the minimization problem (finding one shortest reason) are investigated. Experiments conducted on various datasets reveal the existence of a trade-off between runtime complexity and sparsity. Sufficient reasons - for which the identification problem is DP-complete - are slightly larger than majoritary reasons that can be generated using a simple linear- time greedy algorithm, and significantly larger than minimal majoritary reasons that can be approached using an anytime P ARTIAL M AX SAT algorithm.

On the Computational Intelligibility of Boolean Classifiers

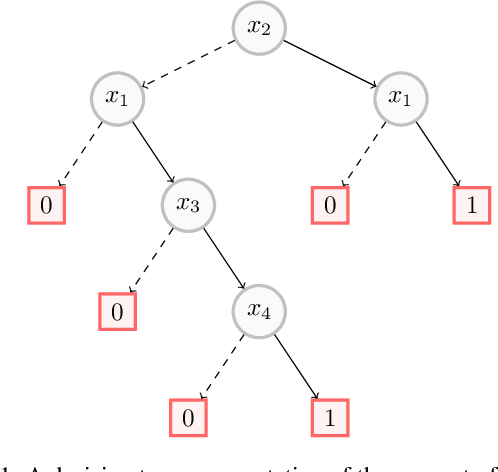
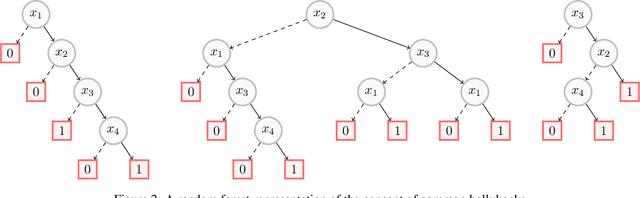
In this paper, we investigate the computational intelligibility of Boolean classifiers, characterized by their ability to answer XAI queries in polynomial time. The classifiers under consideration are decision trees, DNF formulae, decision lists, decision rules, tree ensembles, and Boolean neural nets. Using 9 XAI queries, including both explanation queries and verification queries, we show the existence of large intelligibility gap between the families of classifiers. On the one hand, all the 9 XAI queries are tractable for decision trees. On the other hand, none of them is tractable for DNF formulae, decision lists, random forests, boosted decision trees, Boolean multilayer perceptrons, and binarized neural networks.

Improving MUC extraction thanks to local search

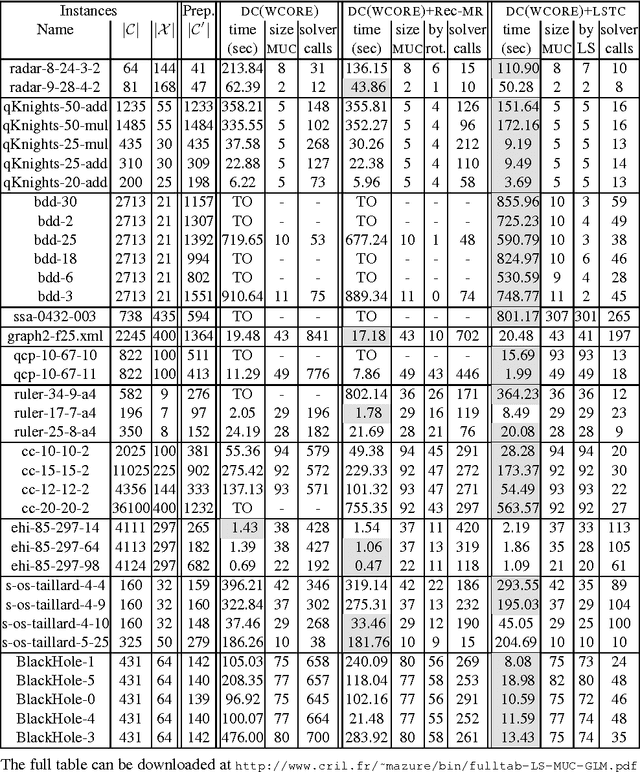
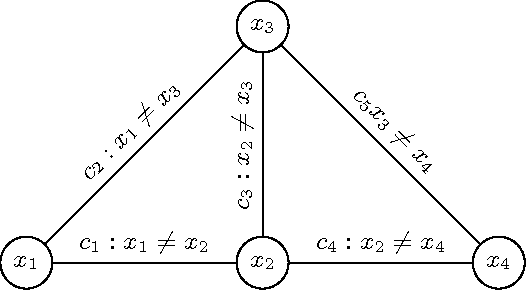
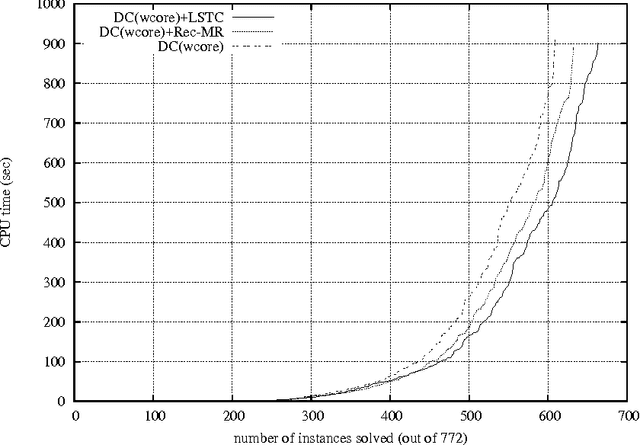
ExtractingMUCs(MinimalUnsatisfiableCores)fromanunsatisfiable constraint network is a useful process when causes of unsatisfiability must be understood so that the network can be re-engineered and relaxed to become sat- isfiable. Despite bad worst-case computational complexity results, various MUC- finding approaches that appear tractable for many real-life instances have been proposed. Many of them are based on the successive identification of so-called transition constraints. In this respect, we show how local search can be used to possibly extract additional transition constraints at each main iteration step. The approach is shown to outperform a technique based on a form of model rotation imported from the SAT-related technology and that also exhibits additional transi- tion constraints. Our extensive computational experimentations show that this en- hancement also boosts the performance of state-of-the-art DC(WCORE)-like MUC extractors.

Integrating Conflict Driven Clause Learning to Local Search

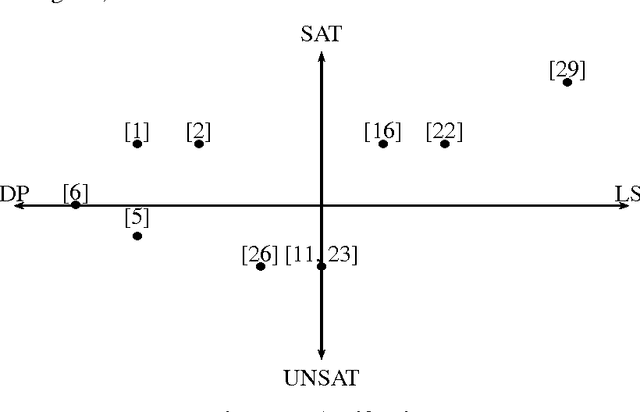
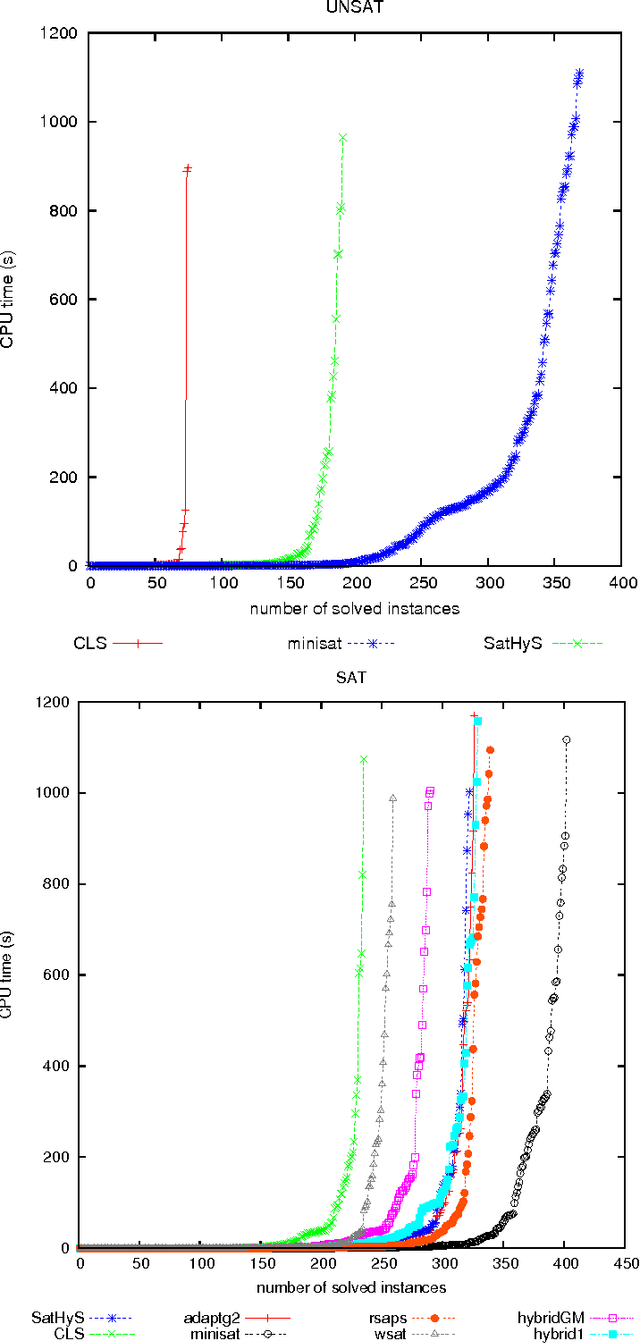
This article introduces SatHyS (SAT HYbrid Solver), a novel hybrid approach for propositional satisfiability. It combines local search and conflict driven clause learning (CDCL) scheme. Each time the local search part reaches a local minimum, the CDCL is launched. For SAT problems it behaves like a tabu list, whereas for UNSAT ones, the CDCL part tries to focus on minimum unsatisfiable sub-formula (MUS). Experimental results show good performances on many classes of SAT instances from the last SAT competitions.