Admissibility in Strength-based Argumentation: Complexity and Algorithms (Extended Version with Proofs)

Recently, Strength-based Argumentation Frameworks (StrAFs) have been proposed to model situations where some quantitative strength is associated with arguments. In this setting, the notion of accrual corresponds to sets of arguments that collectively attack an argument. Some semantics have already been defined, which are sensitive to the existence of accruals that collectively defeat their target, while their individual elements cannot. However, until now, only the surface of this framework and semantics have been studied. Indeed, the existing literature focuses on the adaptation of the stable semantics to StrAFs. In this paper, we push forward the study and investigate the adaptation of admissibility-based semantics. Especially, we show that the strong admissibility defined in the literature does not satisfy a desirable property, namely Dung's fundamental lemma. We therefore propose an alternative definition that induces semantics that behave as expected. We then study computational issues for these new semantics, in particular we show that complexity of reasoning is similar to the complexity of the corresponding decision problems for standard argumentation frameworks in almost all cases. We then propose a translation in pseudo-Boolean constraints for computing (strong and weak) extensions. We conclude with an experimental evaluation of our approach which shows in particular that it scales up well for solving the problem of providing one extension as well as enumerating them all.

Design and Results of ICCMA 2021

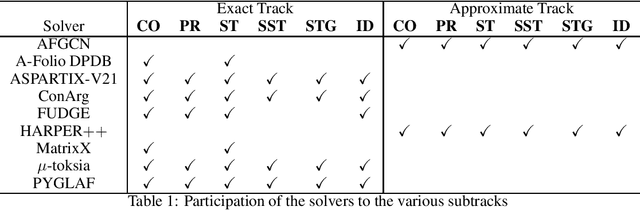
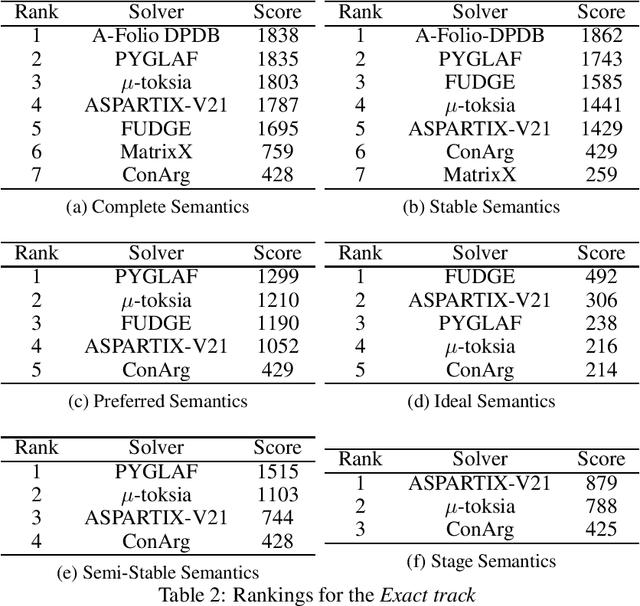
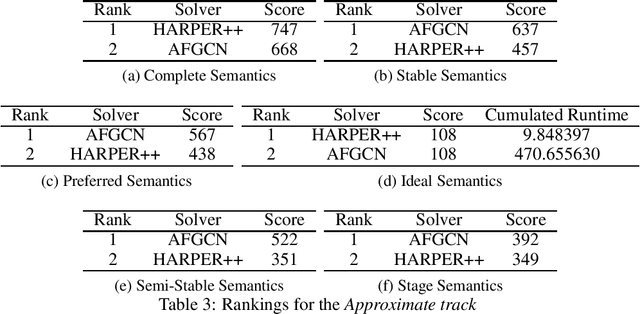
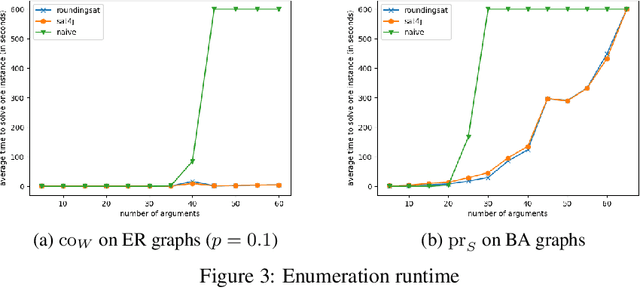
Since 2015, the International Competition on Computational Models of Argumentation (ICCMA) provides a systematic comparison of the different algorithms for solving some classical reasoning problems in the domain of abstract argumentation. This paper discusses the design of the Fourth International Competition on Computational Models of Argumentation. We describe the rules of the competition and the benchmark selection method that we used. After a brief presentation of the competitors, we give an overview of the results.

Stability in Abstract Argumentation

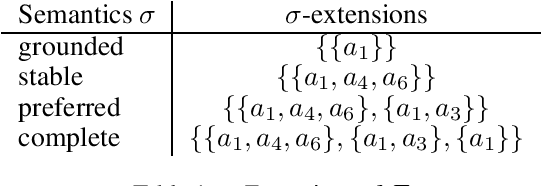
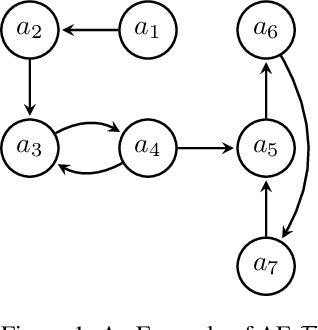
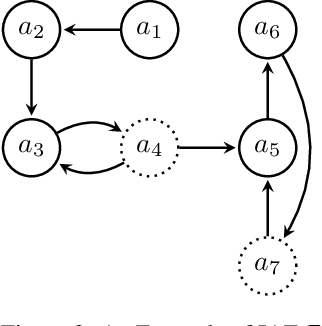
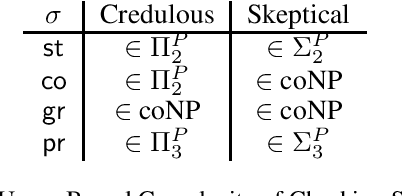
The notion of stability in a structured argumentation setup characterizes situations where the acceptance status associated with a given literal will not be impacted by any future evolution of this setup. In this paper, we abstract away from the logical structure of arguments, and we transpose this notion of stability to the context of Dungean argumentation frameworks. In particular, we show how this problem can be translated into reasoning with Argument-Incomplete AFs. Then we provide preliminary complexity results for stability under four prominent semantics, in the case of both credulous and skeptical reasoning. Finally, we illustrate to what extent this notion can be useful with an application to argument-based negotiation.