Proceedings of the 2024 XCSP3 Competition

This document represents the proceedings of the 2024 XCSP3 Competition. The results of this competition of constraint solvers were presented at CP'24 (30th International Conference on Principles and Practice of Constraint Programming).

Proceedings of the 2023 XCSP3 Competition

This document represents the proceedings of the 2023 XCSP3 Competition. The results of this competition of constraint solvers were presented at CP'23 (the 29th International Conference on Principles and Practice of Constraint Programming, held in Toronto, Canada from 27th to 31th August, 2023).

Proceedings of the 2022 XCSP3 Competition

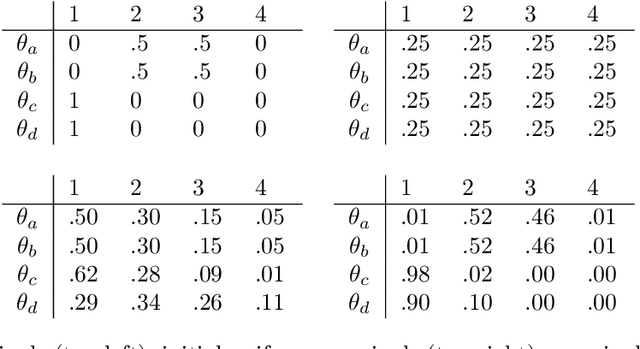
This document represents the proceedings of the 2022 XCSP3 Competition. The results of this competition of constraint solvers were presented at FLOC (Federated Logic Conference) 2022 Olympic Games, held in Haifa, Israel from 31th July 2022 to 7th August, 2022.

Pseudo Polynomial-Time Top-k Algorithms for d-DNNF Circuits

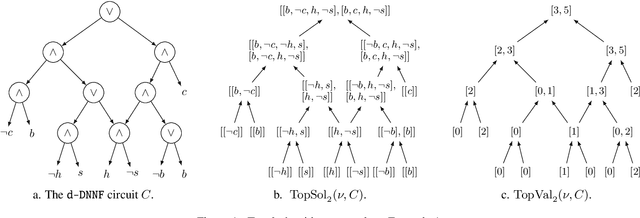
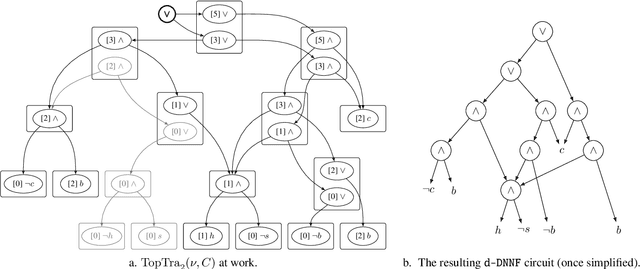
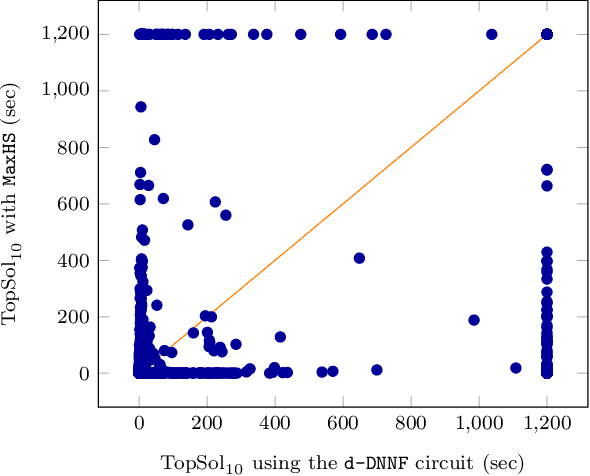
We are interested in computing $k$ most preferred models of a given d-DNNF circuit $C$, where the preference relation is based on an algebraic structure called a monotone, totally ordered, semigroup $(K, \otimes, <)$. In our setting, every literal in $C$ has a value in $K$ and the value of an assignment is an element of $K$ obtained by aggregating using $\otimes$ the values of the corresponding literals. We present an algorithm that computes $k$ models of $C$ among those having the largest values w.r.t. $<$, and show that this algorithm runs in time polynomial in $k$ and in the size of $C$. We also present a pseudo polynomial-time algorithm for deriving the top-$k$ values that can be reached, provided that an additional (but not very demanding) requirement on the semigroup is satisfied. Under the same assumption, we present a pseudo polynomial-time algorithm that transforms $C$ into a d-DNNF circuit $C'$ satisfied exactly by the models of $C$ having a value among the top-$k$ ones. Finally, focusing on the semigroup $(\mathbb{N}, +, <)$, we compare on a large number of instances the performances of our compilation-based algorithm for computing $k$ top solutions with those of an algorithm tackling the same problem, but based on a partial weighted MaxSAT solver.

Design and Results of ICCMA 2021

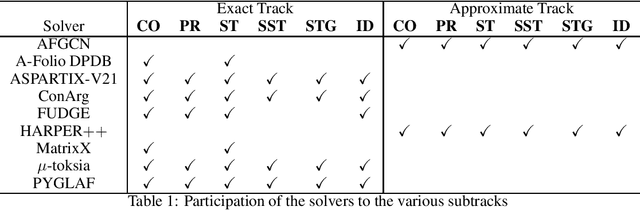
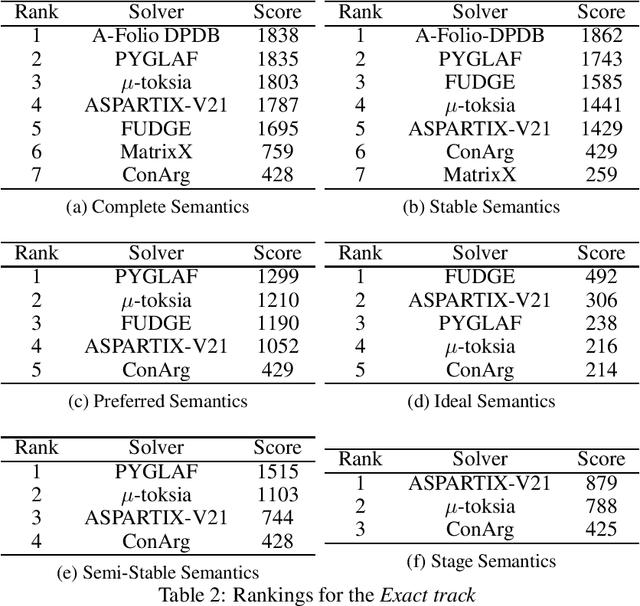
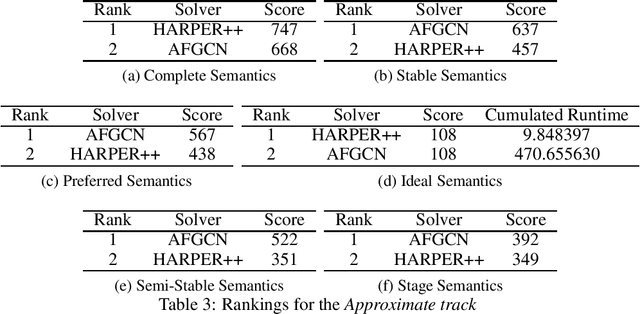
Since 2015, the International Competition on Computational Models of Argumentation (ICCMA) provides a systematic comparison of the different algorithms for solving some classical reasoning problems in the domain of abstract argumentation. This paper discusses the design of the Fourth International Competition on Computational Models of Argumentation. We describe the rules of the competition and the benchmark selection method that we used. After a brief presentation of the competitors, we give an overview of the results.

On the Complexity of Optimization Problems based on Compiled NNF Representations

Optimization is a key task in a number of applications. When the set of feasible solutions under consideration is of combinatorial nature and described in an implicit way as a set of constraints, optimization is typically NP-hard. Fortunately, in many problems, the set of feasible solutions does not often change and is independent from the user's request. In such cases, compiling the set of constraints describing the set of feasible solutions during an off-line phase makes sense, if this compilation step renders computationally easier the generation of a non-dominated, yet feasible solution matching the user's requirements and preferences (which are only known at the on-line step). In this article, we focus on propositional constraints. The subsets L of the NNF language analyzed in Darwiche and Marquis' knowledge compilation map are considered. A number of families F of representations of objective functions over propositional variables, including linear pseudo-Boolean functions and more sophisticated ones, are considered. For each language L and each family F, the complexity of generating an optimal solution when the constraints are compiled into L and optimality is to be considered w.r.t. a function from F is identified.