Pseudo Polynomial-Time Top-k Algorithms for d-DNNF Circuits
Paper and Code
Feb 11, 2022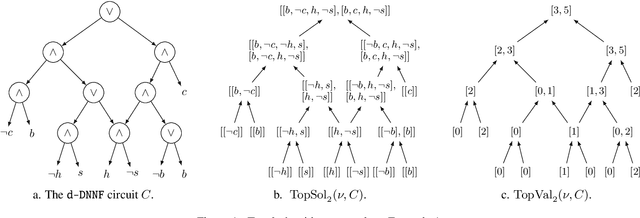

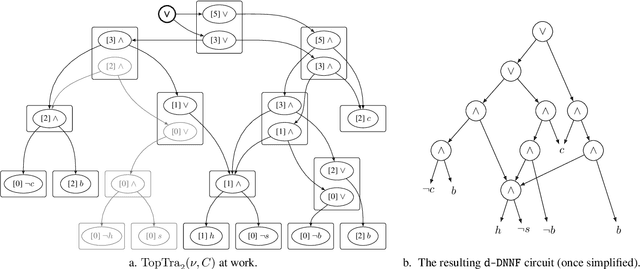
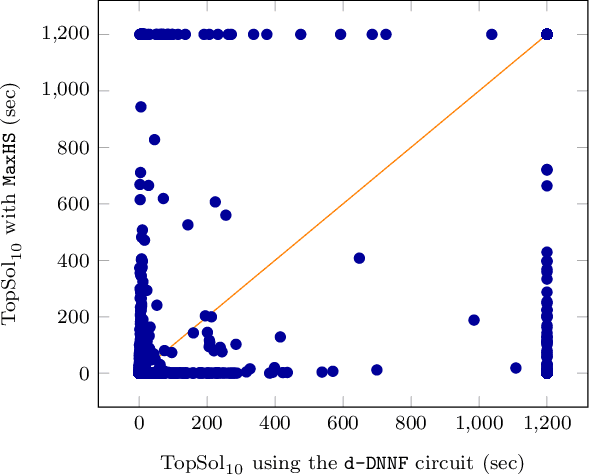
We are interested in computing $k$ most preferred models of a given d-DNNF circuit $C$, where the preference relation is based on an algebraic structure called a monotone, totally ordered, semigroup $(K, \otimes, <)$. In our setting, every literal in $C$ has a value in $K$ and the value of an assignment is an element of $K$ obtained by aggregating using $\otimes$ the values of the corresponding literals. We present an algorithm that computes $k$ models of $C$ among those having the largest values w.r.t. $<$, and show that this algorithm runs in time polynomial in $k$ and in the size of $C$. We also present a pseudo polynomial-time algorithm for deriving the top-$k$ values that can be reached, provided that an additional (but not very demanding) requirement on the semigroup is satisfied. Under the same assumption, we present a pseudo polynomial-time algorithm that transforms $C$ into a d-DNNF circuit $C'$ satisfied exactly by the models of $C$ having a value among the top-$k$ ones. Finally, focusing on the semigroup $(\mathbb{N}, +, <)$, we compare on a large number of instances the performances of our compilation-based algorithm for computing $k$ top solutions with those of an algorithm tackling the same problem, but based on a partial weighted MaxSAT solver.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge