Query Answering with Transitive and Linear-Ordered Data

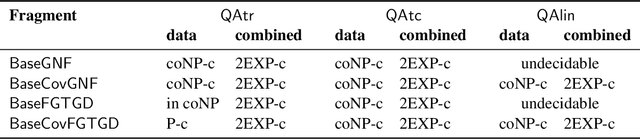
We consider entailment problems involving powerful constraint languages such as frontier-guarded existential rules in which we impose additional semantic restrictions on a set of distinguished relations. We consider restricting a relation to be transitive, restricting a relation to be the transitive closure of another relation, and restricting a relation to be a linear order. We give some natural variants of guardedness that allow inference to be decidable in each case, and isolate the complexity of the corresponding decision problems. Finally we show that slight changes in these conditions lead to undecidability.

Pseudo Polynomial-Time Top-k Algorithms for d-DNNF Circuits

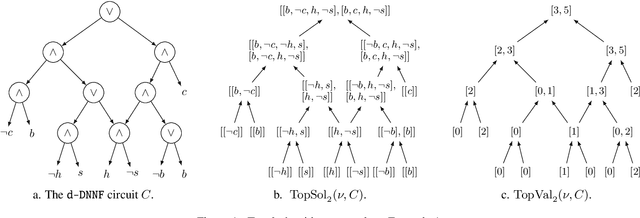
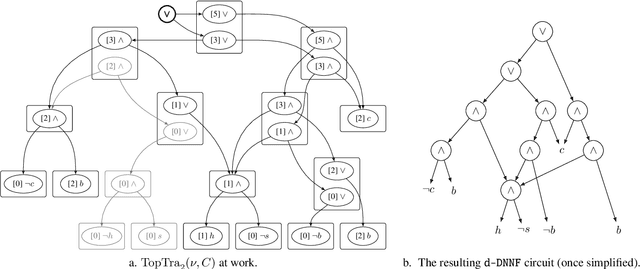
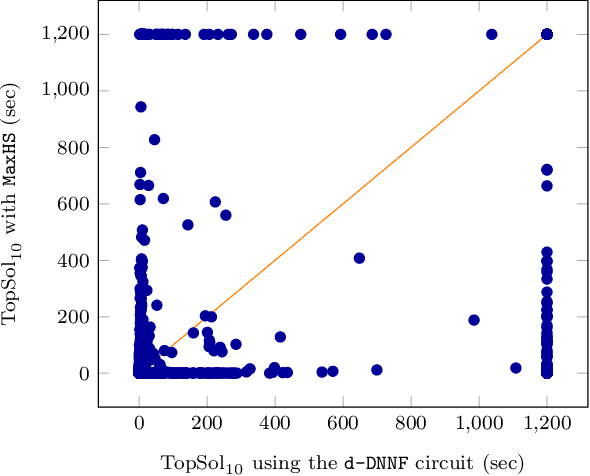
We are interested in computing $k$ most preferred models of a given d-DNNF circuit $C$, where the preference relation is based on an algebraic structure called a monotone, totally ordered, semigroup $(K, \otimes, <)$. In our setting, every literal in $C$ has a value in $K$ and the value of an assignment is an element of $K$ obtained by aggregating using $\otimes$ the values of the corresponding literals. We present an algorithm that computes $k$ models of $C$ among those having the largest values w.r.t. $<$, and show that this algorithm runs in time polynomial in $k$ and in the size of $C$. We also present a pseudo polynomial-time algorithm for deriving the top-$k$ values that can be reached, provided that an additional (but not very demanding) requirement on the semigroup is satisfied. Under the same assumption, we present a pseudo polynomial-time algorithm that transforms $C$ into a d-DNNF circuit $C'$ satisfied exactly by the models of $C$ having a value among the top-$k$ ones. Finally, focusing on the semigroup $(\mathbb{N}, +, <)$, we compare on a large number of instances the performances of our compilation-based algorithm for computing $k$ top solutions with those of an algorithm tackling the same problem, but based on a partial weighted MaxSAT solver.

Containment in Monadic Disjunctive Datalog, MMSNP, and Expressive Description Logics

We study query containment in three closely related formalisms: monadic disjunctive Datalog (MDDLog), MMSNP (a logical generalization of constraint satisfaction problems), and ontology-mediated queries (OMQs) based on expressive description logics and unions of conjunctive queries. Containment in MMSNP was known to be decidable due to a result by Feder and Vardi, but its exact complexity has remained open. We prove 2NEXPTIME-completeness and extend this result to monadic disjunctive Datalog and to OMQs.

Oblivious and Semi-Oblivious Boundedness for Existential Rules

We study the notion of boundedness in the context of positive existential rules, that is, whether there exists an upper bound to the depth of the chase procedure, that is independent from the initial instance. By focussing our attention on the oblivious and the semi-oblivious chase variants, we give a characterization of boundedness in terms of FO-rewritability and chase termination. We show that it is decidable to recognize if a set of rules is bounded for several classes and outline the complexity of the problem. This report contains the paper published at IJCAI 2019 and an appendix with full proofs.

Reasoning about disclosure in data integration in the presence of source constraints

Data integration systems allow users to access data sitting in multiple sources by means of queries over a global schema, related to the sources via mappings. Data sources often contain sensitive information, and thus an analysis is needed to verify that a schema satisfies a privacy policy, given as a set of queries whose answers should not be accessible to users. Such an analysis should take into account not only knowledge that an attacker may have about the mappings, but also what they may know about the semantics of the sources. In this paper, we show that source constraints can have a dramatic impact on disclosure analysis. We study the problem of determining whether a given data integration system discloses a source query to an attacker in the presence of constraints, providing both lower and upper bounds on source-aware disclosure analysis.