Query Answering with Transitive and Linear-Ordered Data

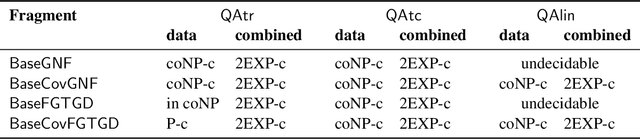
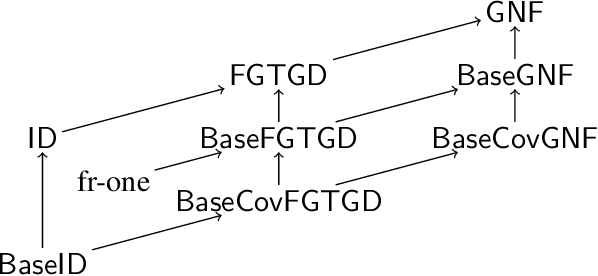
We consider entailment problems involving powerful constraint languages such as frontier-guarded existential rules in which we impose additional semantic restrictions on a set of distinguished relations. We consider restricting a relation to be transitive, restricting a relation to be the transitive closure of another relation, and restricting a relation to be a linear order. We give some natural variants of guardedness that allow inference to be decidable in each case, and isolate the complexity of the corresponding decision problems. Finally we show that slight changes in these conditions lead to undecidability.

Smoothing Structured Decomposable Circuits

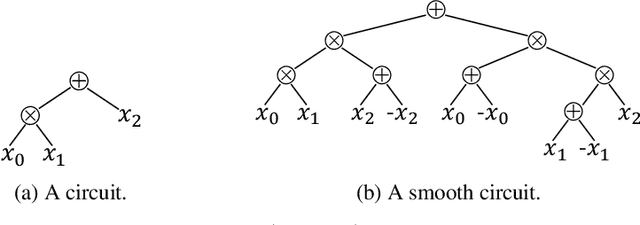
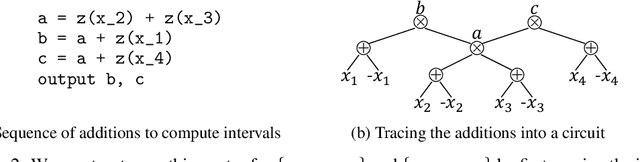
We study the task of smoothing a circuit, i.e., ensuring that all children of a plus-gate mention the same variables. Circuits serve as the building blocks of state-of-the-art inference algorithms on discrete probabilistic graphical models and probabilistic programs. They are also important for discrete density estimation algorithms. Many of these tasks require the input circuit to be smooth. However, smoothing has not been studied in its own right yet, and only a trivial quadratic algorithm is known. This paper studies efficient smoothing for structured decomposable circuits. We propose a near-linear time algorithm for this task and explore lower bounds for smoothing general circuits, using existing results on range-sum queries. Further, for the important special case of All-Marginals, we show a more efficient linear-time algorithm. We validate experimentally the performance of our methods.