Graph neural network outputs are almost surely asymptotically constant

Graph neural networks (GNNs) are the predominant architectures for a variety of learning tasks on graphs. We present a new angle on the expressive power of GNNs by studying how the predictions of a GNN probabilistic classifier evolve as we apply it on larger graphs drawn from some random graph model. We show that the output converges to a constant function, which upper-bounds what these classifiers can express uniformly. This convergence phenomenon applies to a very wide class of GNNs, including state of the art models, with aggregates including mean and the attention-based mechanism of graph transformers. Our results apply to a broad class of random graph models, including the (sparse) Erd\H{o}s-R\'enyi model and the stochastic block model. We empirically validate these findings, observing that the convergence phenomenon already manifests itself on graphs of relatively modest size.

Towards Unbiased Exploration in Partial Label Learning

We consider learning a probabilistic classifier from partially-labelled supervision (inputs denoted with multiple possibilities) using standard neural architectures with a softmax as the final layer. We identify a bias phenomenon that can arise from the softmax layer in even simple architectures that prevents proper exploration of alternative options, making the dynamics of gradient descent overly sensitive to initialisation. We introduce a novel loss function that allows for unbiased exploration within the space of alternative outputs. We give a theoretical justification for our loss function, and provide an extensive evaluation of its impact on synthetic data, on standard partially labelled benchmarks and on a contributed novel benchmark related to an existing rule learning challenge.

Query Answering with Transitive and Linear-Ordered Data

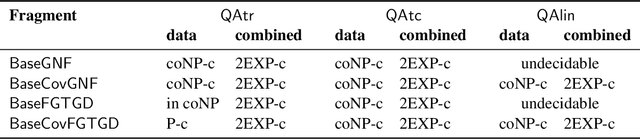
We consider entailment problems involving powerful constraint languages such as frontier-guarded existential rules in which we impose additional semantic restrictions on a set of distinguished relations. We consider restricting a relation to be transitive, restricting a relation to be the transitive closure of another relation, and restricting a relation to be a linear order. We give some natural variants of guardedness that allow inference to be decidable in each case, and isolate the complexity of the corresponding decision problems. Finally we show that slight changes in these conditions lead to undecidability.

Reasoning about disclosure in data integration in the presence of source constraints

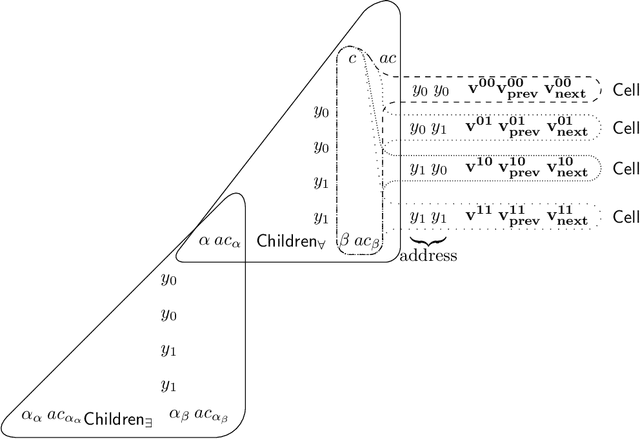
Data integration systems allow users to access data sitting in multiple sources by means of queries over a global schema, related to the sources via mappings. Data sources often contain sensitive information, and thus an analysis is needed to verify that a schema satisfies a privacy policy, given as a set of queries whose answers should not be accessible to users. Such an analysis should take into account not only knowledge that an attacker may have about the mappings, but also what they may know about the semantics of the sources. In this paper, we show that source constraints can have a dramatic impact on disclosure analysis. We study the problem of determining whether a given data integration system discloses a source query to an attacker in the presence of constraints, providing both lower and upper bounds on source-aware disclosure analysis.

Goal-Driven Query Answering for Existential Rules with Equality

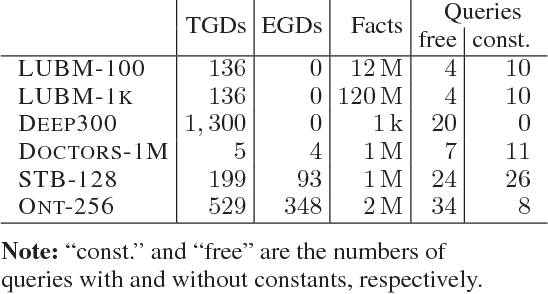
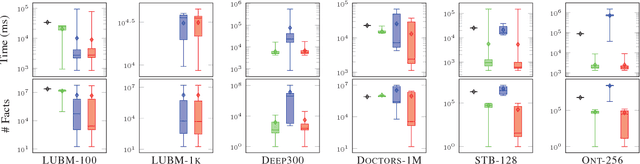
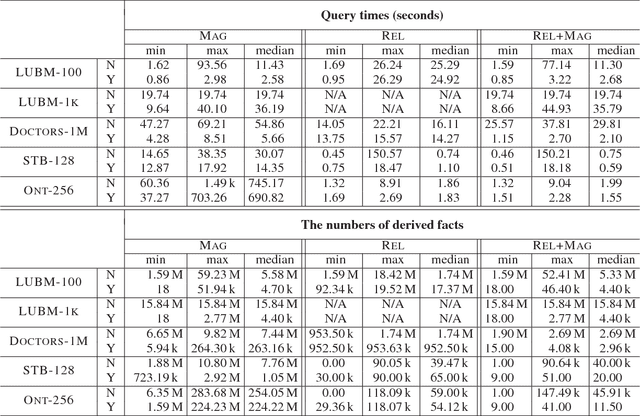
Inspired by the magic sets for Datalog, we present a novel goal-driven approach for answering queries over terminating existential rules with equality (aka TGDs and EGDs). Our technique improves the performance of query answering by pruning the consequences that are not relevant for the query. This is challenging in our setting because equalities can potentially affect all predicates in a dataset. We address this problem by combining the existing singularization technique with two new ingredients: an algorithm for identifying the rules relevant to a query and a new magic sets algorithm. We show empirically that our technique can significantly improve the performance of query answering, and that it can mean the difference between answering a query in a few seconds or not being able to process the query at all.