Goal-Driven Query Answering over First- and Second-Order Dependencies with Equality

Query answering over data with dependencies plays a central role in most applications of dependencies. The problem is commonly solved by using a suitable variant of the chase algorithm to compute a universal model of the dependencies and the data and thus explicate all knowledge implicit in the dependencies. After this preprocessing step, an arbitrary conjunctive query over the dependencies and the data can be answered by evaluating it the computed universal model. If, however, the query to be answered is fixed and known in advance, computing the universal model is often inefficient as many inferences made during this process can be irrelevant to a given query. In such cases, a goal-driven approach, which avoids drawing unnecessary inferences, promises to be more efficient and thus preferable in practice. In this paper we present what we believe to be the first technique for goal-driven query answering over first- and second-order dependencies with equality reasoning. Our technique transforms the input dependencies so that applying the chase to the output avoids many inferences that are irrelevant to the query. The transformation proceeds in several steps, which comprise the following three novel techniques. First, we present a variant of the singularisation technique by Marnette [60] that is applicable to second-order dependencies and that corrects an incompleteness of a related formulation by ten Cate et al. [74]. Second, we present a relevance analysis technique that can eliminate from the input dependencies that provably do not contribute to query answers. Third, we present a variant of the magic sets algorithm [19] that can handle second-order dependencies with equality reasoning. We also present the results of an extensive empirical evaluation, which show that goal-driven query answering can be orders of magnitude faster than computing the full universal model.

On the Correspondence Between Monotonic Max-Sum GNNs and Datalog

Although there has been significant interest in applying machine learning techniques to structured data, the expressivity (i.e., a description of what can be learned) of such techniques is still poorly understood. In this paper, we study data transformations based on graph neural networks (GNNs). First, we note that the choice of how a dataset is encoded into a numeric form processable by a GNN can obscure the characterisation of a model's expressivity, and we argue that a canonical encoding provides an appropriate basis. Second, we study the expressivity of monotonic max-sum GNNs, which cover a subclass of GNNs with max and sum aggregation functions. We show that, for each such GNN, one can compute a Datalog program such that applying the GNN to any dataset produces the same facts as a single round of application of the program's rules to the dataset. Monotonic max-sum GNNs can sum an unbounded number of feature vectors which can result in arbitrarily large feature values, whereas rule application requires only a bounded number of constants. Hence, our result shows that the unbounded summation of monotonic max-sum GNNs does not increase their expressive power. Third, we sharpen our result to the subclass of monotonic max GNNs, which use only the max aggregation function, and identify a corresponding class of Datalog programs.

Datalog Reasoning over Compressed RDF Knowledge Bases

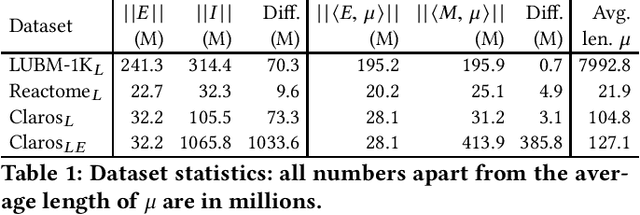
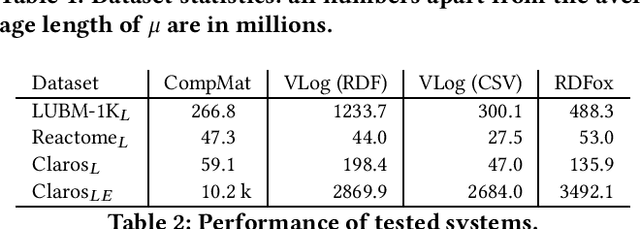
Materialisation is often used in RDF systems as a preprocessing step to derive all facts implied by given RDF triples and rules. Although widely used, materialisation considers all possible rule applications and can use a lot of memory for storing the derived facts, which can hinder performance. We present a novel materialisation technique that compresses the RDF triples so that the rules can sometimes be applied to multiple facts at once, and the derived facts can be represented using structure sharing. Our technique can thus require less space, as well as skip certain rule applications. Our experiments show that our technique can be very effective: when the rules are relatively simple, our system is both faster and requires less memory than prominent state-of-the-art RDF systems.

Modular Materialisation of Datalog Programs

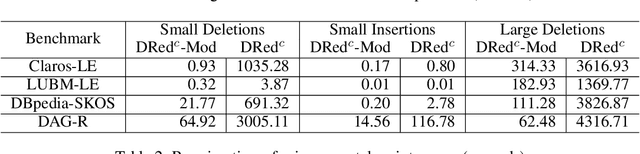
The semina\"ive algorithm can materialise all consequences of arbitrary datalog rules, and it also forms the basis for incremental algorithms that update a materialisation as the input facts change. Certain (combinations of) rules, however, can be handled much more efficiently using custom algorithms. To integrate such algorithms into a general reasoning approach that can handle arbitrary rules, we propose a modular framework for materialisation computation and its maintenance. We split a datalog program into modules that can be handled using specialised algorithms, and handle the remaining rules using the semina\"ive algorithm. We also present two algorithms for computing the transitive and the symmetric-transitive closure of a relation that can be used within our framework. Finally, we show empirically that our framework can handle arbitrary datalog programs while outperforming existing approaches, often by orders of magnitude.

Stratified Negation in Limit Datalog Programs

There has recently been an increasing interest in declarative data analysis, where analytic tasks are specified using a logical language, and their implementation and optimisation are delegated to a general-purpose query engine. Existing declarative languages for data analysis can be formalised as variants of logic programming equipped with arithmetic function symbols and/or aggregation, and are typically undecidable. In prior work, the language of $\mathit{limit\ programs}$ was proposed, which is sufficiently powerful to capture many analysis tasks and has decidable entailment problem. Rules in this language, however, do not allow for negation. In this paper, we study an extension of limit programs with stratified negation-as-failure. We show that the additional expressive power makes reasoning computationally more demanding, and provide tight data complexity bounds. We also identify a fragment with tractable data complexity and sufficient expressivity to capture many relevant tasks.

Goal-Driven Query Answering for Existential Rules with Equality

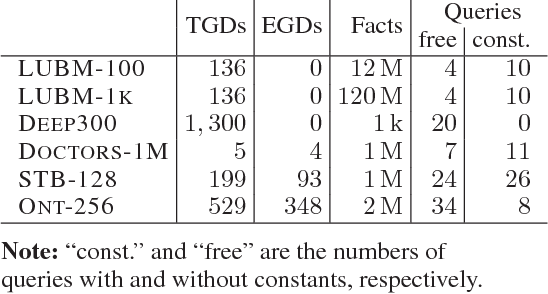
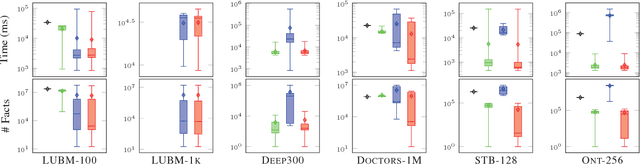
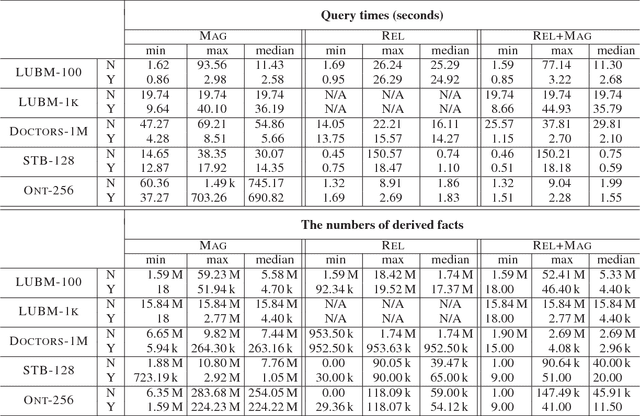
Inspired by the magic sets for Datalog, we present a novel goal-driven approach for answering queries over terminating existential rules with equality (aka TGDs and EGDs). Our technique improves the performance of query answering by pruning the consequences that are not relevant for the query. This is challenging in our setting because equalities can potentially affect all predicates in a dataset. We address this problem by combining the existing singularization technique with two new ingredients: an algorithm for identifying the rules relevant to a query and a new magic sets algorithm. We show empirically that our technique can significantly improve the performance of query answering, and that it can mean the difference between answering a query in a few seconds or not being able to process the query at all.

Optimised Maintenance of Datalog Materialisations

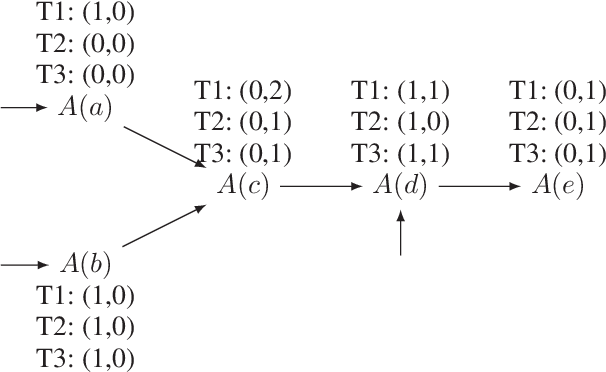
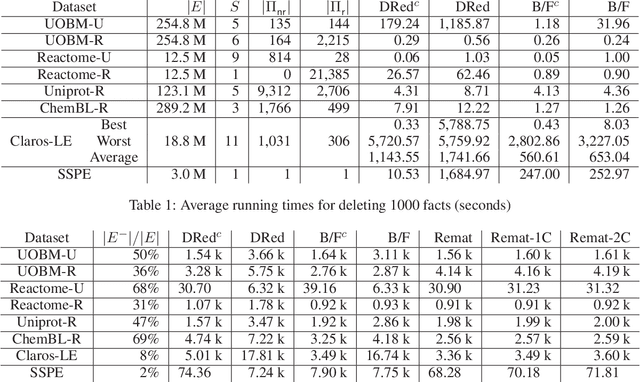
To efficiently answer queries, datalog systems often materialise all consequences of a datalog program, so the materialisation must be updated whenever the input facts change. Several solutions to the materialisation update problem have been proposed. The Delete/Rederive (DRed) and the Backward/Forward (B/F) algorithms solve this problem for general datalog, but both contain steps that evaluate rules 'backwards' by matching their heads to a fact and evaluating the partially instantiated rule bodies as queries. We show that this can be a considerable source of overhead even on very small updates. In contrast, the Counting algorithm does not evaluate the rules 'backwards', but it can handle only nonrecursive rules. We present two hybrid approaches that combine DRed and B/F with Counting so as to reduce or even eliminate 'backward' rule evaluation while still handling arbitrary datalog programs. We show empirically that our hybrid algorithms are usually significantly faster than existing approaches, sometimes by orders of magnitude.

Foundations of Declarative Data Analysis Using Limit Datalog Programs

Motivated by applications in declarative data analysis, we study $\mathit{Datalog}_{\mathbb{Z}}$---an extension of positive Datalog with arithmetic functions over integers. This language is known to be undecidable, so we propose two fragments. In $\mathit{limit}~\mathit{Datalog}_{\mathbb{Z}}$ predicates are axiomatised to keep minimal/maximal numeric values, allowing us to show that fact entailment is coNExpTime-complete in combined, and coNP-complete in data complexity. Moreover, an additional $\mathit{stability}$ requirement causes the complexity to drop to ExpTime and PTime, respectively. Finally, we show that stable $\mathit{Datalog}_{\mathbb{Z}}$ can express many useful data analysis tasks, and so our results provide a sound foundation for the development of advanced information systems.

Stream Reasoning in Temporal Datalog

In recent years, there has been an increasing interest in extending traditional stream processing engines with logical, rule-based, reasoning capabilities. This poses significant theoretical and practical challenges since rules can derive new information and propagate it both towards past and future time points; as a result, streamed query answers can depend on data that has not yet been received, as well as on data that arrived far in the past. Stream reasoning algorithms, however, must be able to stream out query answers as soon as possible, and can only keep a limited number of previous input facts in memory. In this paper, we propose novel reasoning problems to deal with these challenges, and study their computational properties on Datalog extended with a temporal sort and the successor function (a core rule-based language for stream reasoning applications).

Extending Consequence-Based Reasoning to SRIQ

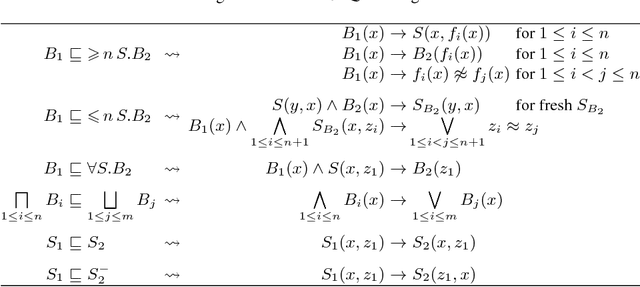
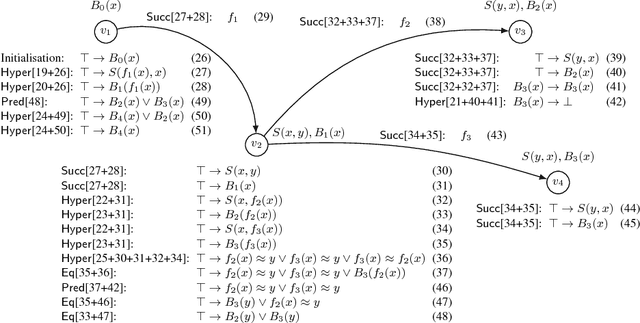
Consequence-based calculi are a family of reasoning algorithms for description logics (DLs), and they combine hypertableau and resolution in a way that often achieves excellent performance in practice. Up to now, however, they were proposed for either Horn DLs (which do not support disjunction), or for DLs without counting quantifiers. In this paper we present a novel consequence-based calculus for SRIQ---a rich DL that supports both features. This extension is non-trivial since the intermediate consequences that need to be derived during reasoning cannot be captured using DLs themselves. The results of our preliminary performance evaluation suggest the feasibility of our approach in practice.