Modular Materialisation of Datalog Programs
Paper and Code
Nov 13, 2018
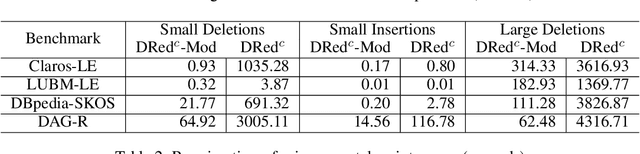
The semina\"ive algorithm can materialise all consequences of arbitrary datalog rules, and it also forms the basis for incremental algorithms that update a materialisation as the input facts change. Certain (combinations of) rules, however, can be handled much more efficiently using custom algorithms. To integrate such algorithms into a general reasoning approach that can handle arbitrary rules, we propose a modular framework for materialisation computation and its maintenance. We split a datalog program into modules that can be handled using specialised algorithms, and handle the remaining rules using the semina\"ive algorithm. We also present two algorithms for computing the transitive and the symmetric-transitive closure of a relation that can be used within our framework. Finally, we show empirically that our framework can handle arbitrary datalog programs while outperforming existing approaches, often by orders of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge