Tractable Offline Learning of Regular Decision Processes

This work studies offline Reinforcement Learning (RL) in a class of non-Markovian environments called Regular Decision Processes (RDPs). In RDPs, the unknown dependency of future observations and rewards from the past interactions can be captured by some hidden finite-state automaton. For this reason, many RDP algorithms first reconstruct this unknown dependency using automata learning techniques. In this paper, we show that it is possible to overcome two strong limitations of previous offline RL algorithms for RDPs, notably RegORL. This can be accomplished via the introduction of two original techniques: the development of a new pseudometric based on formal languages, which removes a problematic dependency on $L_\infty^\mathsf{p}$-distinguishability parameters, and the adoption of Count-Min-Sketch (CMS), instead of naive counting. The former reduces the number of samples required in environments that are characterized by a low complexity in language-theoretic terms. The latter alleviates the memory requirements for long planning horizons. We derive the PAC sample complexity bounds associated to each of these techniques, and we validate the approach experimentally.

On The Expressivity of Recurrent Neural Cascades

Recurrent Neural Cascades (RNCs) are the recurrent neural networks with no cyclic dependencies among recurrent neurons. This class of recurrent networks has received a lot of attention in practice. Besides training methods for a fixed architecture such as backpropagation, the cascade architecture naturally allows for constructive learning methods, where recurrent nodes are added incrementally one at a time, often yielding smaller networks. Furthermore, acyclicity amounts to a structural prior that even for the same number of neurons yields a more favourable sample complexity compared to a fully-connected architecture. A central question is whether the advantages of the cascade architecture come at the cost of a reduced expressivity. We provide new insights into this question. We show that the regular languages captured by RNCs with sign and tanh activation with positive recurrent weights are the star-free regular languages. In order to establish our results we developed a novel framework where capabilities of RNCs are accessed by analysing which semigroups and groups a single neuron is able to implement. A notable implication of our framework is that RNCs can achieve the expressivity of all regular languages by introducing neurons that can implement groups.

The Krohn-Rhodes Logics

We present a new family of modal temporal logics of the past, obtained by extending Past LTL with a rich set of temporal operators based on the theory by Krohn and Rhodes for automata cascades. The theory says that every automaton can be expressed as a cascade of some basic automata called prime automata. They are the building blocks of all automata, analogously to prime numbers being the building blocks of all natural numbers. We show that Past LTL corresponds to cascades of one kind of prime automata called flip-flops. In particular, the temporal operators of Past LTL are captured by flip-flops, and they cannot capture any other prime automaton, confining the expressivity within the star-free regular languages. We propose novel temporal operators that can capture other prime automata, and hence extend the expressivity of Past LTL. Such operators are infinitely-many, and they yield an infinite number of logics capturing an infinite number of distinct fragments of the regular languages. The result is a yet unexplored landscape of extensions of Past LTL, that we call Krohn-Rhodes Logics, each of them with the potential of matching the expressivity required by specific applications.

Sample Complexity of Automata Cascades

Every automaton can be decomposed into a cascade of basic automata. This is the Prime Decomposition Theorem by Krohn and Rhodes. We show that cascades allow for describing the sample complexity of automata in terms of their components. In particular, we show that the sample complexity is linear in the number of components and the maximum complexity of a single component, modulo logarithmic factors. This opens to the possibility of learning automata representing large dynamical systems consisting of many parts interacting with each other. It is in sharp contrast with the established understanding of the sample complexity of automata, described in terms of the overall number of states and input letters, which implies that it is only possible to learn automata where the number of states is linear in the amount of data available. Instead our results show that one can learn automata with a number of states that is exponential in the amount of data available.

Markov Abstractions for PAC Reinforcement Learning in Non-Markov Decision Processes

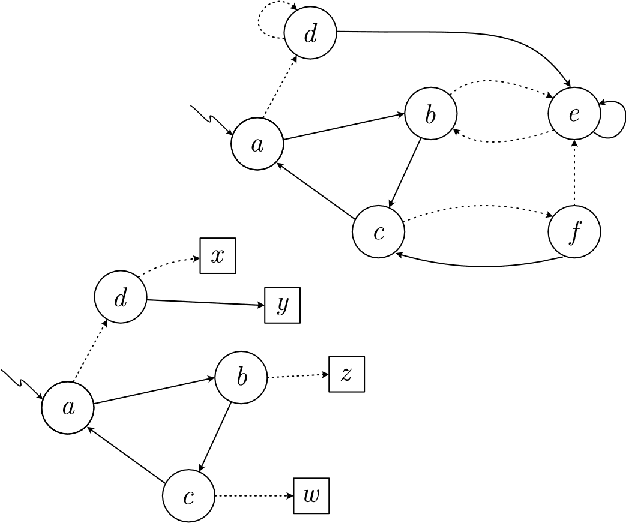
Our work aims at developing reinforcement learning algorithms that do not rely on the Markov assumption. We consider the class of Non-Markov Decision Processes where histories can be abstracted into a finite set of states while preserving the dynamics. We call it a Markov abstraction since it induces a Markov Decision Process over a set of states that encode the non-Markov dynamics. This phenomenon underlies the recently introduced Regular Decision Processes (as well as POMDPs where only a finite number of belief states is reachable). In all such kinds of decision process, an agent that uses a Markov abstraction can rely on the Markov property to achieve optimal behaviour. We show that Markov abstractions can be learned during reinforcement learning. For these two tasks, any algorithms satisfying some basic requirements can be employed. We show that our approach has PAC guarantees when the employed algorithms have PAC guarantees, and we also provide an experimental evaluation.

Efficient PAC Reinforcement Learning in Regular Decision Processes

Recently regular decision processes have been proposed as a well-behaved form of non-Markov decision process. Regular decision processes are characterised by a transition function and a reward function that depend on the whole history, though regularly (as in regular languages). In practice both the transition and the reward functions can be seen as finite transducers. We study reinforcement learning in regular decision processes. Our main contribution is to show that a near-optimal policy can be PAC-learned in polynomial time in a set of parameters that describe the underlying decision process. We argue that the identified set of parameters is minimal and it reasonably captures the difficulty of a regular decision process.

The Window Validity Problem in Rule-Based Stream Reasoning

Rule-based temporal query languages provide the expressive power and flexibility required to capture in a natural way complex analysis tasks over streaming data. Stream processing applications, however, typically require near real-time response using limited resources. In particular, it becomes essential that the underpinning query language has favourable computational properties and that stream processing algorithms are able to keep only a small number of previously received facts in memory at any point in time without sacrificing correctness. In this paper, we propose a recursive fragment of temporal Datalog with tractable data complexity and study the properties of a generic stream reasoning algorithm for this fragment. We focus on the window validity problem as a way to minimise the number of time points for which the stream reasoning algorithm needs to keep data in memory at any point in time.

Stream Reasoning in Temporal Datalog

In recent years, there has been an increasing interest in extending traditional stream processing engines with logical, rule-based, reasoning capabilities. This poses significant theoretical and practical challenges since rules can derive new information and propagate it both towards past and future time points; as a result, streamed query answers can depend on data that has not yet been received, as well as on data that arrived far in the past. Stream reasoning algorithms, however, must be able to stream out query answers as soon as possible, and can only keep a limited number of previous input facts in memory. In this paper, we propose novel reasoning problems to deal with these challenges, and study their computational properties on Datalog extended with a temporal sort and the successor function (a core rule-based language for stream reasoning applications).

Improved Answer-Set Programming Encodings for Abstract Argumentation

The design of efficient solutions for abstract argumentation problems is a crucial step towards advanced argumentation systems. One of the most prominent approaches in the literature is to use Answer-Set Programming (ASP) for this endeavor. In this paper, we present new encodings for three prominent argumentation semantics using the concept of conditional literals in disjunctions as provided by the ASP-system clingo. Our new encodings are not only more succinct than previous versions, but also outperform them on standard benchmarks.