Markov Abstractions for PAC Reinforcement Learning in Non-Markov Decision Processes

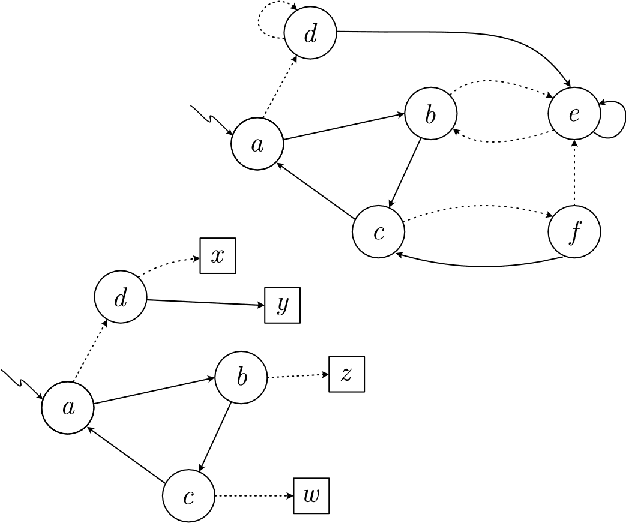
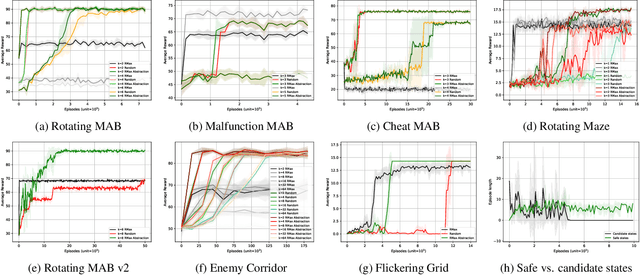
Our work aims at developing reinforcement learning algorithms that do not rely on the Markov assumption. We consider the class of Non-Markov Decision Processes where histories can be abstracted into a finite set of states while preserving the dynamics. We call it a Markov abstraction since it induces a Markov Decision Process over a set of states that encode the non-Markov dynamics. This phenomenon underlies the recently introduced Regular Decision Processes (as well as POMDPs where only a finite number of belief states is reachable). In all such kinds of decision process, an agent that uses a Markov abstraction can rely on the Markov property to achieve optimal behaviour. We show that Markov abstractions can be learned during reinforcement learning. For these two tasks, any algorithms satisfying some basic requirements can be employed. We show that our approach has PAC guarantees when the employed algorithms have PAC guarantees, and we also provide an experimental evaluation.