Giuseppe De Giacomo
Sapienza University of Rome, Italy
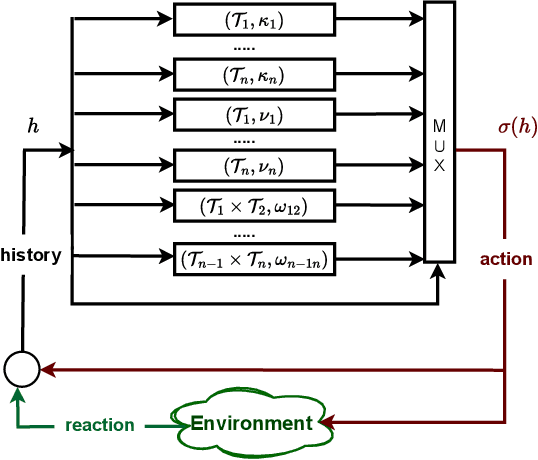
Semantically Labelled Automata for Multi-Task Reinforcement Learning with LTL Instructions
Feb 06, 2026Abstract:We study multi-task reinforcement learning (RL), a setting in which an agent learns a single, universal policy capable of generalising to arbitrary, possibly unseen tasks. We consider tasks specified as linear temporal logic (LTL) formulae, which are commonly used in formal methods to specify properties of systems, and have recently been successfully adopted in RL. In this setting, we present a novel task embedding technique leveraging a new generation of semantic LTL-to-automata translations, originally developed for temporal synthesis. The resulting semantically labelled automata contain rich, structured information in each state that allow us to (i) compute the automaton efficiently on-the-fly, (ii) extract expressive task embeddings used to condition the policy, and (iii) naturally support full LTL. Experimental results in a variety of domains demonstrate that our approach achieves state-of-the-art performance and is able to scale to complex specifications where existing methods fail.
Multi-Property Synthesis
Jan 15, 2026Abstract:We study LTLf synthesis with multiple properties, where satisfying all properties may be impossible. Instead of enumerating subsets of properties, we compute in one fixed-point computation the relation between product-game states and the goal sets that are realizable from them, and we synthesize strategies achieving maximal realizable sets. We develop a fully symbolic algorithm that introduces Boolean goal variables and exploits monotonicity to represent exponentially many goal combinations compactly. Our approach substantially outperforms enumeration-based baselines, with speedups of up to two orders of magnitude.
Good-for-MDP State Reduction for Stochastic LTL Planning
Nov 15, 2025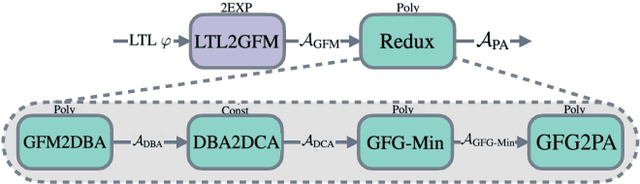
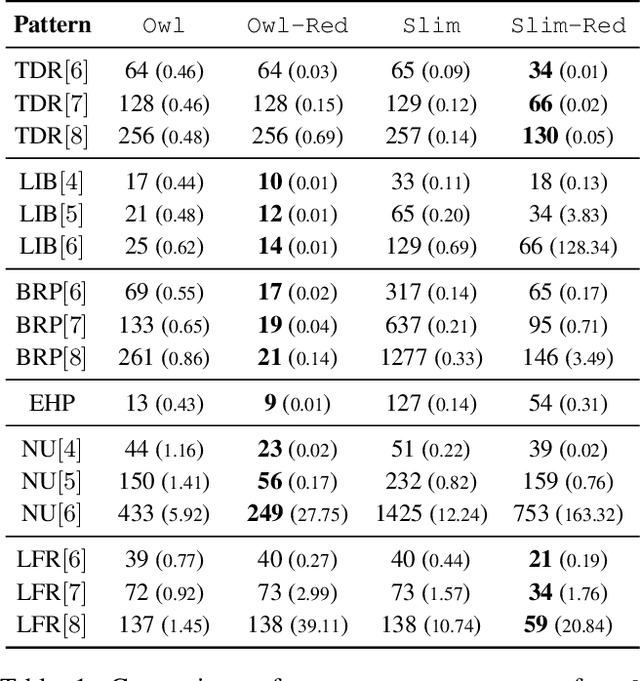
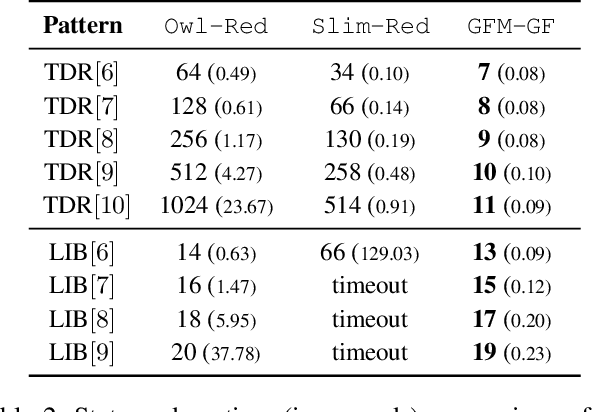
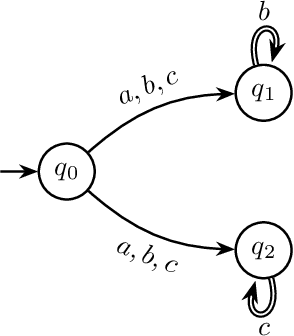
Abstract:We study stochastic planning problems in Markov Decision Processes (MDPs) with goals specified in Linear Temporal Logic (LTL). The state-of-the-art approach transforms LTL formulas into good-for-MDP (GFM) automata, which feature a restricted form of nondeterminism. These automata are then composed with the MDP, allowing the agent to resolve the nondeterminism during policy synthesis. A major factor affecting the scalability of this approach is the size of the generated automata. In this paper, we propose a novel GFM state-space reduction technique that significantly reduces the number of automata states. Our method employs a sophisticated chain of transformations, leveraging recent advances in good-for-games minimisation developed for adversarial settings. In addition to our theoretical contributions, we present empirical results demonstrating the practical effectiveness of our state-reduction technique. Furthermore, we introduce a direct construction method for formulas of the form $\mathsf{G}\mathsf{F}\varphi$, where $\varphi$ is a co-safety formula. This construction is provably single-exponential in the worst case, in contrast to the general doubly-exponential complexity. Our experiments confirm the scalability advantages of this specialised construction.
Emerson-Lei and Manna-Pnueli Games for LTLf+ and PPLTL+ Synthesis
Aug 20, 2025Abstract:Recently, the Manna-Pnueli Hierarchy has been used to define the temporal logics LTLfp and PPLTLp, which allow to use finite-trace LTLf/PPLTL techniques in infinite-trace settings while achieving the expressiveness of full LTL. In this paper, we present the first actual solvers for reactive synthesis in these logics. These are based on games on graphs that leverage DFA-based techniques from LTLf/PPLTL to construct the game arena. We start with a symbolic solver based on Emerson-Lei games, which reduces lower-class properties (guarantee, safety) to higher ones (recurrence, persistence) before solving the game. We then introduce Manna-Pnueli games, which natively embed Manna-Pnueli objectives into the arena. These games are solved by composing solutions to a DAG of simpler Emerson-Lei games, resulting in a provably more efficient approach. We implemented the solvers and practically evaluated their performance on a range of representative formulas. The results show that Manna-Pnueli games often offer significant advantages, though not universally, indicating that combining both approaches could further enhance practical performance.
Best-Effort Policies for Robust Markov Decision Processes
Aug 11, 2025Abstract:We study the common generalization of Markov decision processes (MDPs) with sets of transition probabilities, known as robust MDPs (RMDPs). A standard goal in RMDPs is to compute a policy that maximizes the expected return under an adversarial choice of the transition probabilities. If the uncertainty in the probabilities is independent between the states, known as s-rectangularity, such optimal robust policies can be computed efficiently using robust value iteration. However, there might still be multiple optimal robust policies, which, while equivalent with respect to the worst-case, reflect different expected returns under non-adversarial choices of the transition probabilities. Hence, we propose a refined policy selection criterion for RMDPs, drawing inspiration from the notions of dominance and best-effort in game theory. Instead of seeking a policy that only maximizes the worst-case expected return, we additionally require the policy to achieve a maximal expected return under different (i.e., not fully adversarial) transition probabilities. We call such a policy an optimal robust best-effort (ORBE) policy. We prove that ORBE policies always exist, characterize their structure, and present an algorithm to compute them with a small overhead compared to standard robust value iteration. ORBE policies offer a principled tie-breaker among optimal robust policies. Numerical experiments show the feasibility of our approach.
LTLf Adaptive Synthesis for Multi-Tier Goals in Nondeterministic Domains
Apr 29, 2025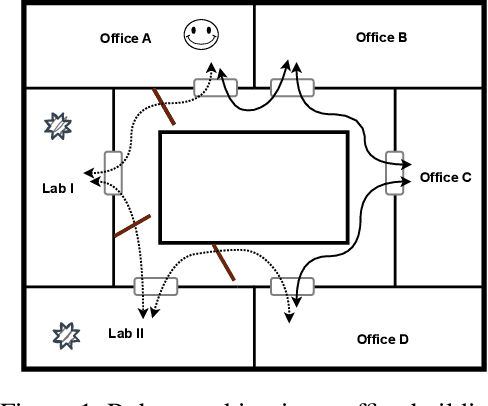
Abstract:We study a variant of LTLf synthesis that synthesizes adaptive strategies for achieving a multi-tier goal, consisting of multiple increasingly challenging LTLf objectives in nondeterministic planning domains. Adaptive strategies are strategies that at any point of their execution (i) enforce the satisfaction of as many objectives as possible in the multi-tier goal, and (ii) exploit possible cooperation from the environment to satisfy as many as possible of the remaining ones. This happens dynamically: if the environment cooperates (ii) and an objective becomes enforceable (i), then our strategies will enforce it. We provide a game-theoretic technique to compute adaptive strategies that is sound and complete. Notably, our technique is polynomial, in fact quadratic, in the number of objectives. In other words, it handles multi-tier goals with only a minor overhead compared to standard LTLf synthesis.
LTLf+ and PPLTL+: Extending LTLf and PPLTL to Infinite Traces
Nov 14, 2024Abstract:We introduce LTLf+ and PPLTL+, two logics to express properties of infinite traces, that are based on the linear-time temporal logics LTLf and PPLTL on finite traces. LTLf+/PPLTL+ use levels of Manna and Pnueli's LTL safety-progress hierarchy, and thus have the same expressive power as LTL. However, they also retain a crucial characteristic of the reactive synthesis problem for the base logics: the game arena for strategy extraction can be derived from deterministic finite automata (DFA). Consequently, these logics circumvent the notorious difficulties associated with determinizing infinite trace automata, typical of LTL reactive synthesis. We present DFA-based synthesis techniques for LTLf+/PPLTL+, and show that synthesis is 2EXPTIME-complete for LTLf+ (matching LTLf) and EXPTIME-complete for PPLTL+ (matching PPLTL). Notably, while PPLTL+ retains the full expressive power of LTL, reactive synthesis is EXPTIME-complete instead of 2EXPTIME-complete. The techniques are also adapted to optimally solve satisfiability, validity, and model-checking, to get EXPSPACE-complete for LTLf+ (extending a recent result for the guarantee level using LTLf), and PSPACE-complete for PPLTL+.
Computational Grounding of Responsibility Attribution and Anticipation in LTLf
Oct 18, 2024Abstract:Responsibility is one of the key notions in machine ethics and in the area of autonomous systems. It is a multi-faceted notion involving counterfactual reasoning about actions and strategies. In this paper, we study different variants of responsibility in a strategic setting based on LTLf. We show a connection with notions in reactive synthesis, including synthesis of winning, dominant, and best-effort strategies. This connection provides the building blocks for a computational grounding of responsibility including complexity characterizations and sound, complete, and optimal algorithms for attributing and anticipating responsibility.
The Trembling-Hand Problem for LTLf Planning
Apr 24, 2024



Abstract:Consider an agent acting to achieve its temporal goal, but with a "trembling hand". In this case, the agent may mistakenly instruct, with a certain (typically small) probability, actions that are not intended due to faults or imprecision in its action selection mechanism, thereby leading to possible goal failure. We study the trembling-hand problem in the context of reasoning about actions and planning for temporally extended goals expressed in Linear Temporal Logic on finite traces (LTLf), where we want to synthesize a strategy (aka plan) that maximizes the probability of satisfying the LTLf goal in spite of the trembling hand. We consider both deterministic and nondeterministic (adversarial) domains. We propose solution techniques for both cases by relying respectively on Markov Decision Processes and on Markov Decision Processes with Set-valued Transitions with LTLf objectives, where the set-valued probabilistic transitions capture both the nondeterminism from the environment and the possible action instruction errors from the agent. We formally show the correctness of our solution techniques and demonstrate their effectiveness experimentally through a proof-of-concept implementation.
Composition of Nondeterministic and Stochastic Services for LTLf Task Specifications
Nov 29, 2023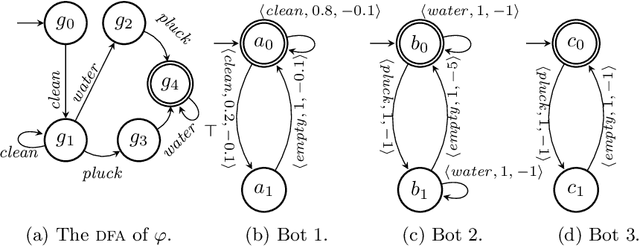
Abstract:In this paper, we study the composition of services so as to obtain runs satisfying a task specification in Linear Temporal Logic on finite traces (LTLf). We study the problem in the case services are nondeterministic and the LTLf specification can be exactly met, and in the case services are stochastic, where we are interested in maximizing the probability of satisfaction of the LTLf specification and, simultaneously, minimizing the utilization cost of the services. To do so, we combine techniques from LTLf synthesis, service composition \`a la Roman Model, reactive synthesis, and bi-objective lexicographic optimization on MDPs. This framework has several interesting applications, including Smart Manufacturing and Digital Twins.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge