The Trembling-Hand Problem for LTLf Planning

Consider an agent acting to achieve its temporal goal, but with a "trembling hand". In this case, the agent may mistakenly instruct, with a certain (typically small) probability, actions that are not intended due to faults or imprecision in its action selection mechanism, thereby leading to possible goal failure. We study the trembling-hand problem in the context of reasoning about actions and planning for temporally extended goals expressed in Linear Temporal Logic on finite traces (LTLf), where we want to synthesize a strategy (aka plan) that maximizes the probability of satisfying the LTLf goal in spite of the trembling hand. We consider both deterministic and nondeterministic (adversarial) domains. We propose solution techniques for both cases by relying respectively on Markov Decision Processes and on Markov Decision Processes with Set-valued Transitions with LTLf objectives, where the set-valued probabilistic transitions capture both the nondeterminism from the environment and the possible action instruction errors from the agent. We formally show the correctness of our solution techniques and demonstrate their effectiveness experimentally through a proof-of-concept implementation.

Understanding Boolean Function Learnability on Deep Neural Networks

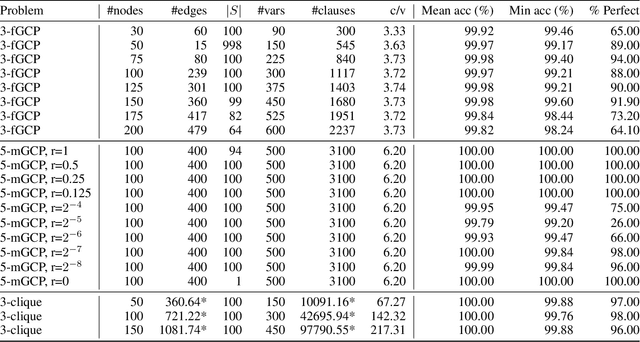
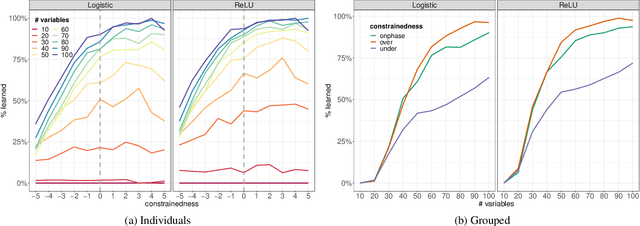
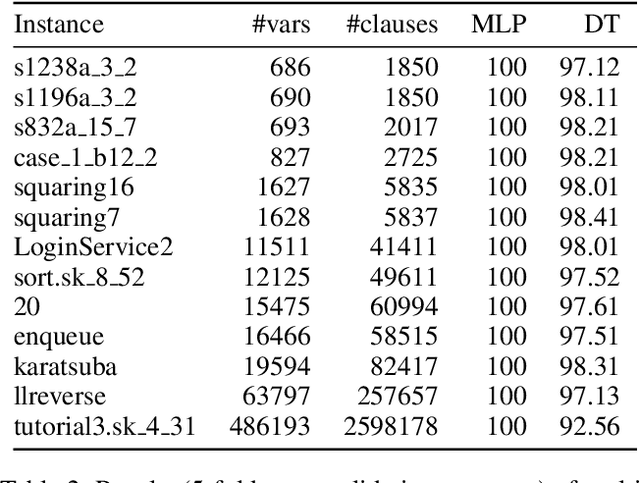
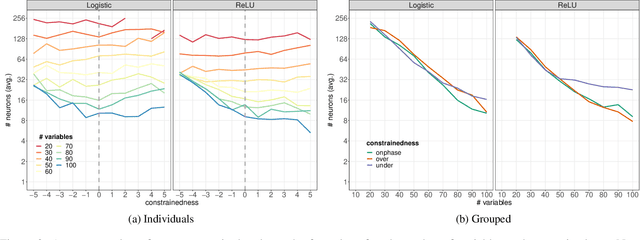
Computational learning theory states that many classes of boolean formulas are learnable in polynomial time. This paper addresses the understudied subject of how, in practice, such formulas can be learned by deep neural networks. Specifically, we analyse boolean formulas associated with the decision version of combinatorial optimisation problems, model sampling benchmarks, and random 3-CNFs with varying degrees of constrainedness. Our extensive experiments indicate that: (i) regardless of the combinatorial optimisation problem, relatively small and shallow neural networks are very good approximators of the associated formulas; (ii) smaller formulas seem harder to learn, possibly due to the fewer positive (satisfying) examples available; and (iii) interestingly, underconstrained 3-CNF formulas are more challenging to learn than overconstrained ones. Source code and relevant datasets are publicly available (https://github.com/machine-reasoning-ufrgs/mlbf).

Graph Neural Networks Meet Neural-Symbolic Computing: A Survey and Perspective

Neural-symbolic computing has now become the subject of interest of both academic and industry research laboratories. Graph Neural Networks (GNN) have been widely used in relational and symbolic domains, with widespread application of GNNs in combinatorial optimization, constraint satisfaction, relational reasoning and other scientific domains. The need for improved explainability, interpretability and trust of AI systems in general demands principled methodologies, as suggested by neural-symbolic computing. In this paper, we review the state-of-the-art on the use of GNNs as a model of neural-symbolic computing. This includes the application of GNNs in several domains as well as its relationship to current developments in neural-symbolic computing.

LTLf Synthesis with Fairness and Stability Assumptions

In synthesis, assumptions are constraints on the environment that rule out certain environment behaviors. A key observation here is that even if we consider systems with LTLf goals on finite traces, environment assumptions need to be expressed over infinite traces, since accomplishing the agent goals may require an unbounded number of environment action. To solve synthesis with respect to finite-trace LTLf goals under infinite-trace assumptions, we could reduce the problem to LTL synthesis. Unfortunately, while synthesis in LTLf and in LTL have the same worst-case complexity (both 2EXPTIME-complete), the algorithms available for LTL synthesis are much more difficult in practice than those for LTLf synthesis. In this work we show that in interesting cases we can avoid such a detour to LTL synthesis and keep the simplicity of LTLf synthesis. Specifically, we develop a BDD-based fixpoint-based technique for handling basic forms of fairness and of stability assumptions. We show, empirically, that this technique performs much better than standard LTL synthesis.

Learning to Solve NP-Complete Problems - A Graph Neural Network for the Decision TSP

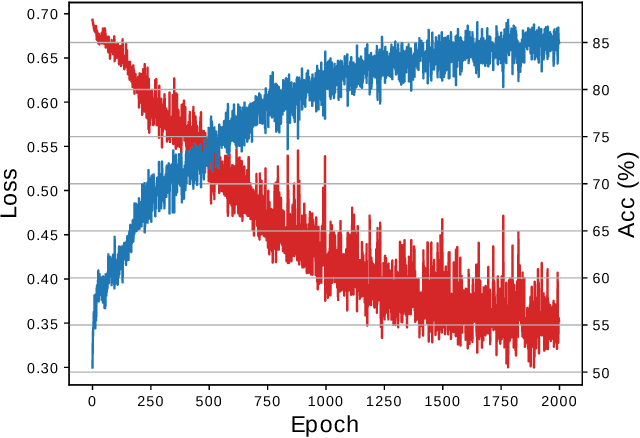
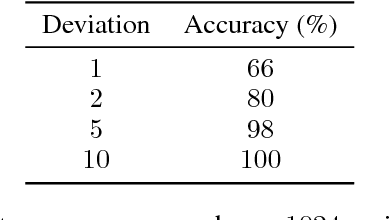
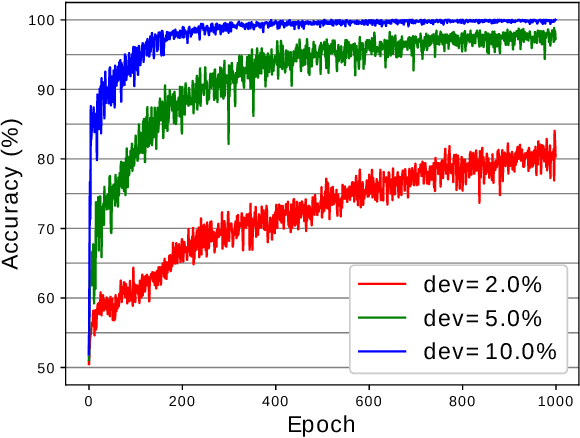
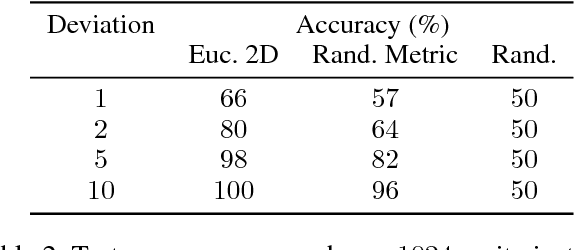
Graph Neural Networks (GNN) are a promising technique for bridging differential programming and combinatorial domains. GNNs employ trainable modules which can be assembled in different configurations that reflect the relational structure of each problem instance. In this paper, we show that GNNs can learn to solve, with very little supervision, the decision variant of the Traveling Salesperson Problem (TSP), a highly relevant $\mathcal{NP}$-Complete problem. Our model is trained to function as an effective message-passing algorithm in which edges (embedded with their weights) communicate with vertices for a number of iterations after which the model is asked to decide whether a route with cost $<C$ exists. We show that such a network can be trained with sets of dual examples: given the optimal tour cost $C^{*}$, we produce one decision instance with target cost $x\%$ smaller and one with target cost $x\%$ larger than $C^{*}$. We were able to obtain $80\%$ accuracy training with $-2\%,+2\%$ deviations, and the same trained model can generalize for more relaxed deviations with increasing performance. We also show that the model is capable of generalizing for larger problem sizes. Finally, we provide a method for predicting the optimal route cost within $2\%$ deviation from the ground truth. In summary, our work shows that Graph Neural Networks are powerful enough to solve $\mathcal{NP}$-Complete problems which combine symbolic and numeric data.

Constrained Sampling and Counting: Universal Hashing Meets SAT Solving

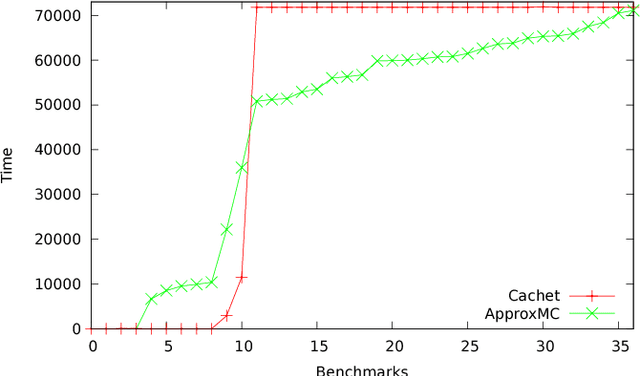
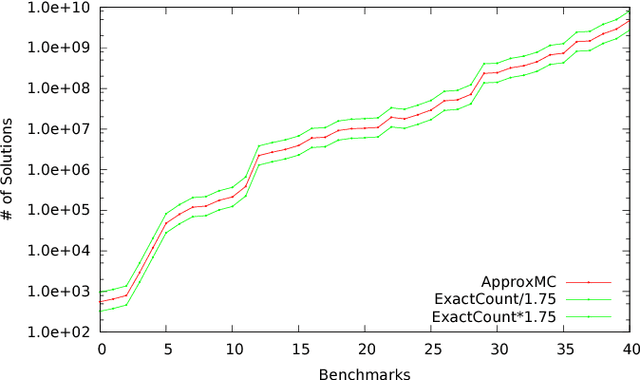
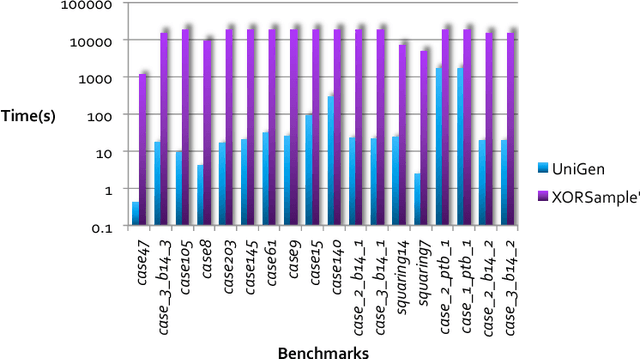
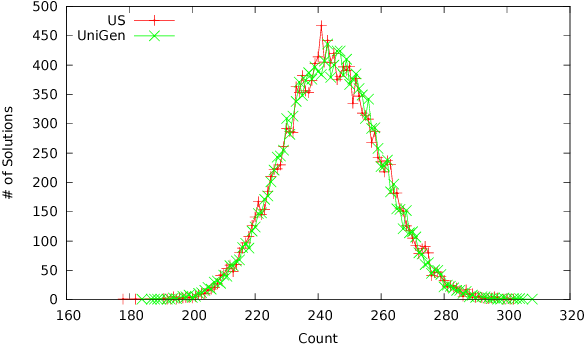
Constrained sampling and counting are two fundamental problems in artificial intelligence with a diverse range of applications, spanning probabilistic reasoning and planning to constrained-random verification. While the theory of these problems was thoroughly investigated in the 1980s, prior work either did not scale to industrial size instances or gave up correctness guarantees to achieve scalability. Recently, we proposed a novel approach that combines universal hashing and SAT solving and scales to formulas with hundreds of thousands of variables without giving up correctness guarantees. This paper provides an overview of the key ingredients of the approach and discusses challenges that need to be overcome to handle larger real-world instances.