Learning to Solve NP-Complete Problems - A Graph Neural Network for the Decision TSP

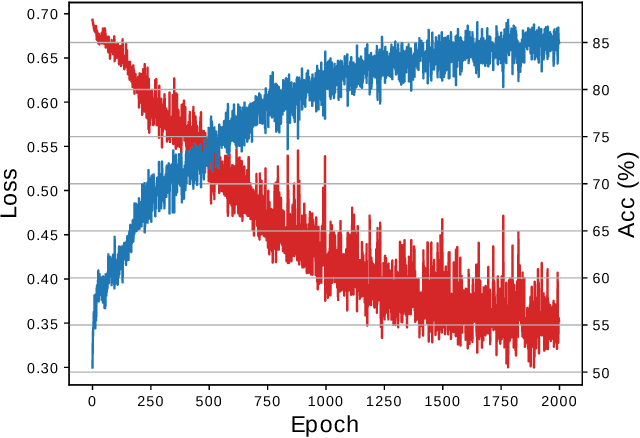
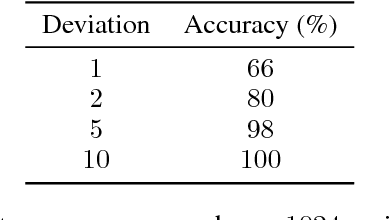
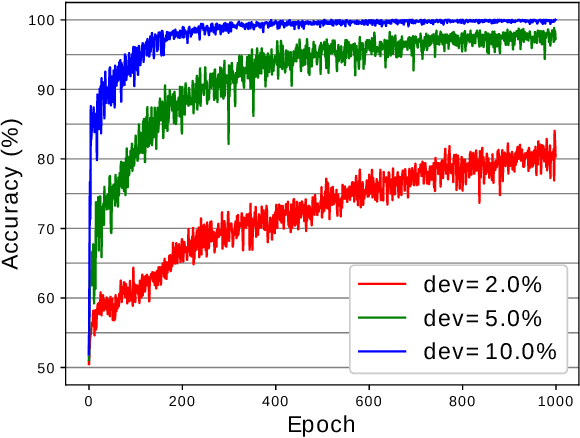
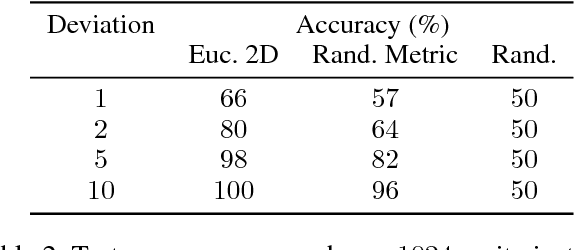
Graph Neural Networks (GNN) are a promising technique for bridging differential programming and combinatorial domains. GNNs employ trainable modules which can be assembled in different configurations that reflect the relational structure of each problem instance. In this paper, we show that GNNs can learn to solve, with very little supervision, the decision variant of the Traveling Salesperson Problem (TSP), a highly relevant $\mathcal{NP}$-Complete problem. Our model is trained to function as an effective message-passing algorithm in which edges (embedded with their weights) communicate with vertices for a number of iterations after which the model is asked to decide whether a route with cost $<C$ exists. We show that such a network can be trained with sets of dual examples: given the optimal tour cost $C^{*}$, we produce one decision instance with target cost $x\%$ smaller and one with target cost $x\%$ larger than $C^{*}$. We were able to obtain $80\%$ accuracy training with $-2\%,+2\%$ deviations, and the same trained model can generalize for more relaxed deviations with increasing performance. We also show that the model is capable of generalizing for larger problem sizes. Finally, we provide a method for predicting the optimal route cost within $2\%$ deviation from the ground truth. In summary, our work shows that Graph Neural Networks are powerful enough to solve $\mathcal{NP}$-Complete problems which combine symbolic and numeric data.