Graph Neural Networks Meet Neural-Symbolic Computing: A Survey and Perspective

Neural-symbolic computing has now become the subject of interest of both academic and industry research laboratories. Graph Neural Networks (GNN) have been widely used in relational and symbolic domains, with widespread application of GNNs in combinatorial optimization, constraint satisfaction, relational reasoning and other scientific domains. The need for improved explainability, interpretability and trust of AI systems in general demands principled methodologies, as suggested by neural-symbolic computing. In this paper, we review the state-of-the-art on the use of GNNs as a model of neural-symbolic computing. This includes the application of GNNs in several domains as well as its relationship to current developments in neural-symbolic computing.

Graph Colouring Meets Deep Learning: Effective Graph Neural Network Models for Combinatorial Problems

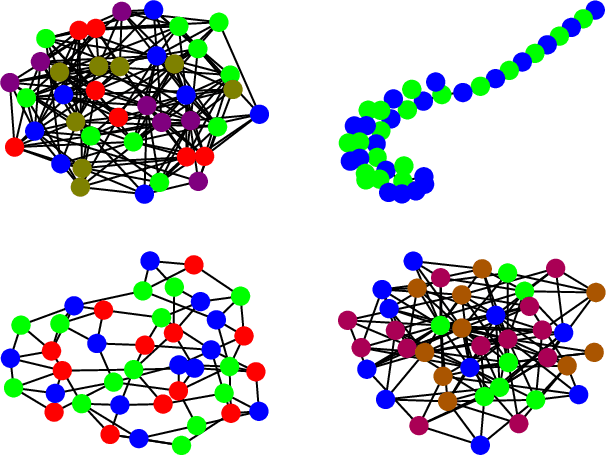
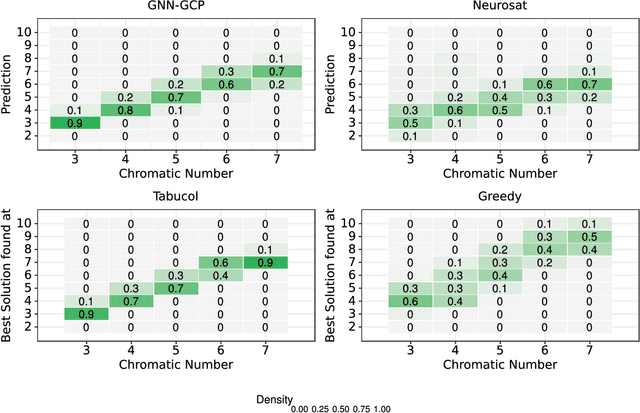
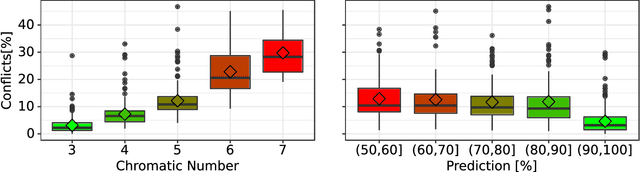
Deep learning has consistently defied state-of-the-art techniques in many fields over the last decade. However, we are just beginning to understand the capabilities of neural learning in symbolic domains. Deep learning architectures that employ parameter sharing over graphs can produce models which can be trained on complex properties of relational data. These include highly relevant NP-Complete problems, such as SAT and TSP. In this work, we showcase how Graph Neural Networks (GNN) can be engineered -- with a very simple architecture -- to solve the fundamental combinatorial problem of graph colouring. Our results show that the model, which achieves high accuracy upon training on random instances, is able to generalise to graph distributions different from those seen at training time. Further, it performs better than the Tabucol and greedy baselines for some distributions. In addition, we show how vertex embeddings can be clustered in multidimensional spaces to yield constructive solutions even though our model is only trained as a binary classifier. In summary, our results contribute to shorten the gap in our understanding of the algorithms learned by GNNs, as well as hoarding empirical evidence for their capability on hard combinatorial problems. Our results thus contribute to the standing challenge of integrating robust learning and symbolic reasoning in Deep Learning systems.

Typed Graph Networks

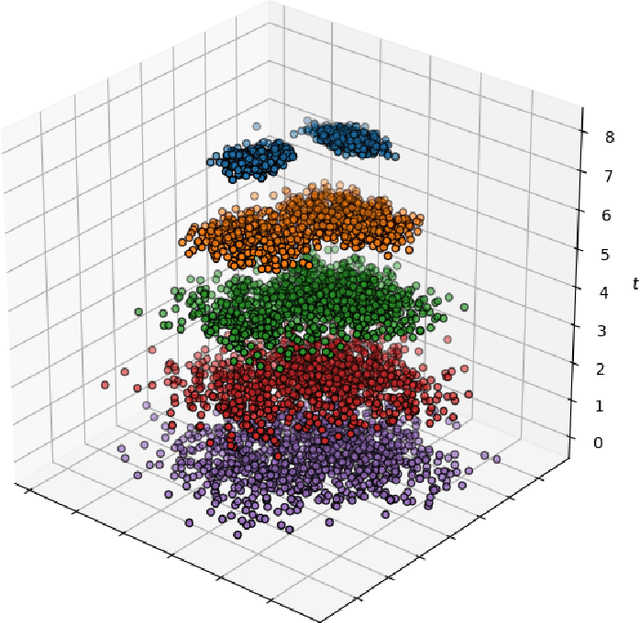
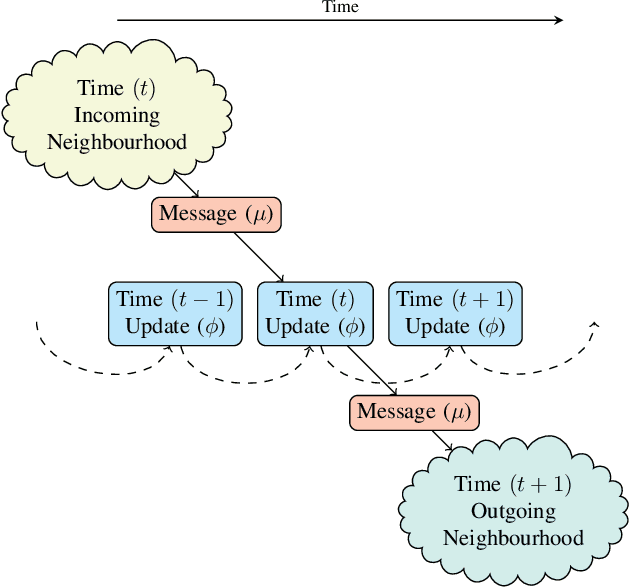
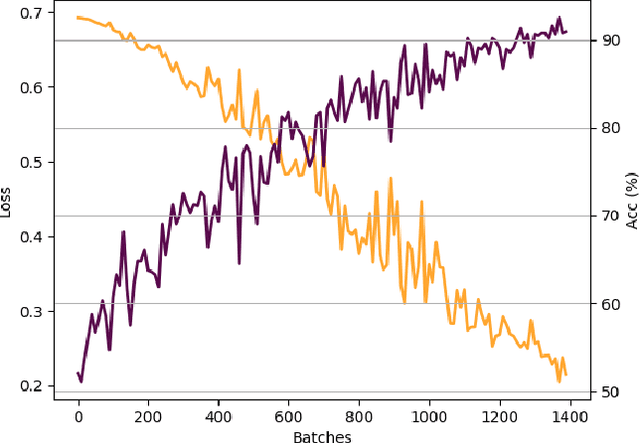
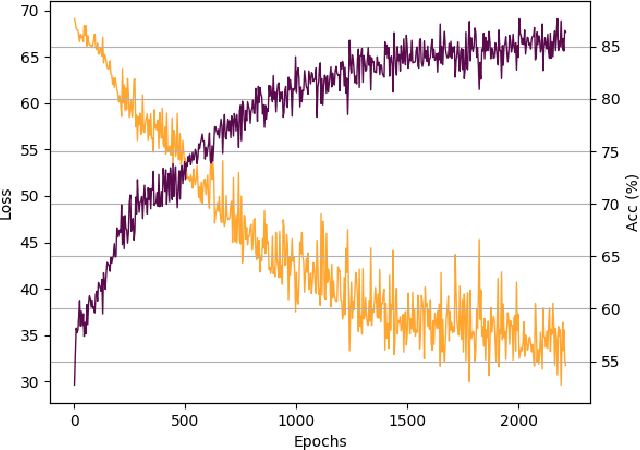
Recently, the deep learning community has given growing attention to neural architectures engineered to learn problems in relational domains. Convolutional Neural Networks employ parameter sharing over the image domain, tying the weights of neural connections on a grid topology and thus enforcing the learning of a number of convolutional kernels. By instantiating trainable neural modules and assembling them in varied configurations (apart from grids), one can enforce parameter sharing over graphs, yielding models which can effectively be fed with relational data. In this context, vertices in a graph can be projected into a hyperdimensional real space and iteratively refined over many message-passing iterations in an end-to-end differentiable architecture. Architectures of this family have been referred to with several definitions in the literature, such as Graph Neural Networks, Message-passing Neural Networks, Relational Networks and Graph Networks. In this paper, we revisit the original Graph Neural Network model and show that it generalises many of the recent models, which in turn benefit from the insight of thinking about vertex \textbf{types}. To illustrate the generality of the original model, we present a Graph Neural Network formalisation, which partitions the vertices of a graph into a number of types. Each type represents an entity in the ontology of the problem one wants to learn. This allows - for instance - one to assign embeddings to edges, hyperedges, and any number of global attributes of the graph. As a companion to this paper we provide a Python/Tensorflow library to facilitate the development of such architectures, with which we instantiate the formalisation to reproduce a number of models proposed in the current literature.

Assessing Gender Bias in Machine Translation -- A Case Study with Google Translate

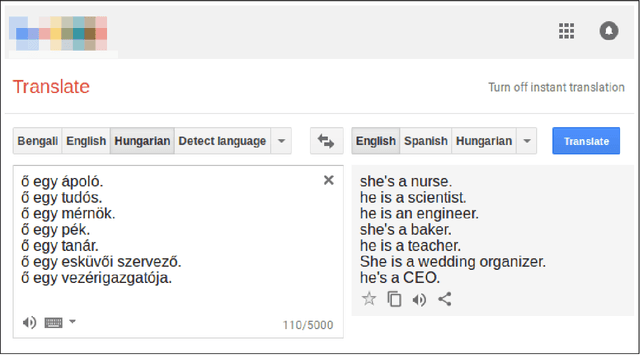
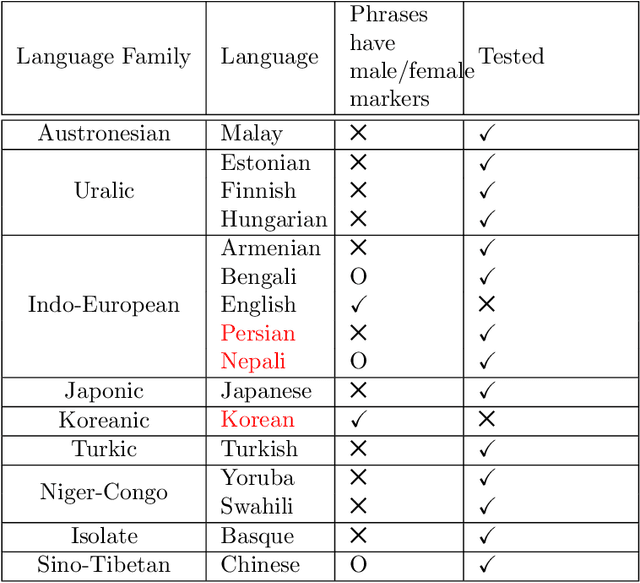
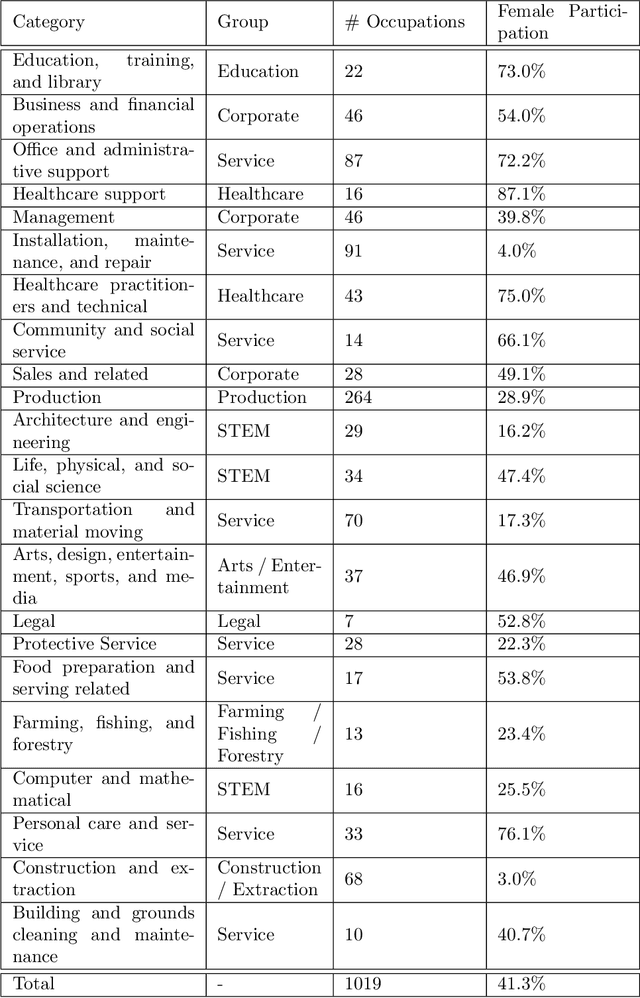
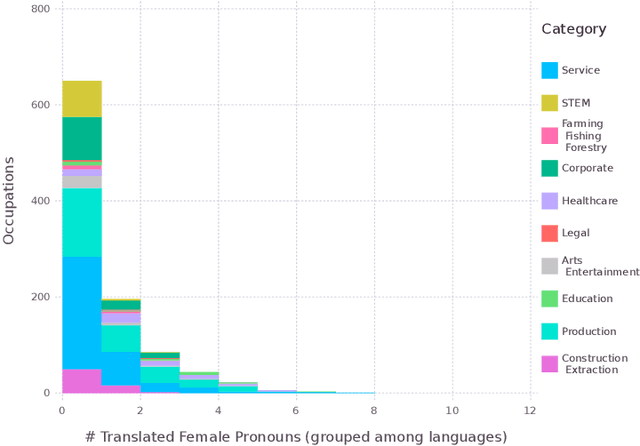
Recently there has been a growing concern about machine bias, where trained statistical models grow to reflect controversial societal asymmetries, such as gender or racial bias. A significant number of AI tools have recently been suggested to be harmfully biased towards some minority, with reports of racist criminal behavior predictors, Iphone X failing to differentiate between two Asian people and Google photos' mistakenly classifying black people as gorillas. Although a systematic study of such biases can be difficult, we believe that automated translation tools can be exploited through gender neutral languages to yield a window into the phenomenon of gender bias in AI. In this paper, we start with a comprehensive list of job positions from the U.S. Bureau of Labor Statistics (BLS) and used it to build sentences in constructions like "He/She is an Engineer" in 12 different gender neutral languages such as Hungarian, Chinese, Yoruba, and several others. We translate these sentences into English using the Google Translate API, and collect statistics about the frequency of female, male and gender-neutral pronouns in the translated output. We show that GT exhibits a strong tendency towards male defaults, in particular for fields linked to unbalanced gender distribution such as STEM jobs. We ran these statistics against BLS' data for the frequency of female participation in each job position, showing that GT fails to reproduce a real-world distribution of female workers. We provide experimental evidence that even if one does not expect in principle a 50:50 pronominal gender distribution, GT yields male defaults much more frequently than what would be expected from demographic data alone. We are hopeful that this work will ignite a debate about the need to augment current statistical translation tools with debiasing techniques which can already be found in the scientific literature.

Learning to Solve NP-Complete Problems - A Graph Neural Network for the Decision TSP

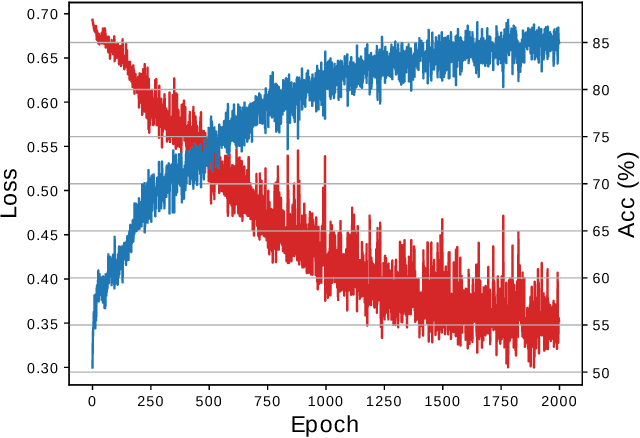
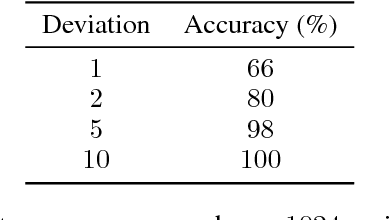
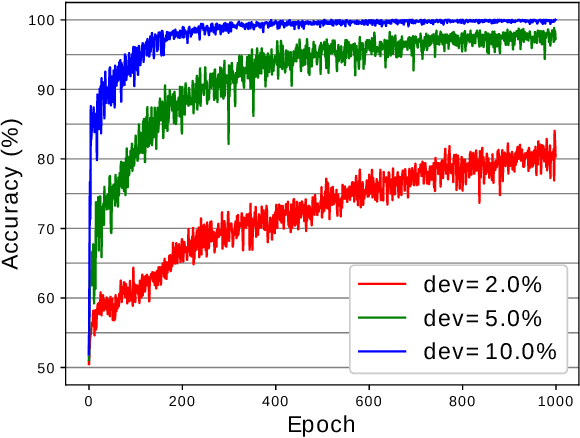
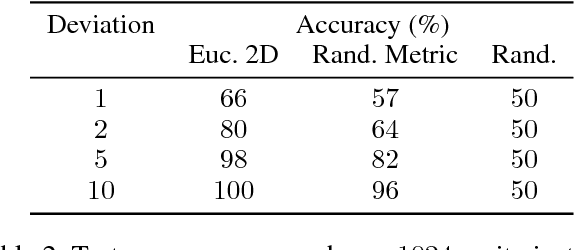
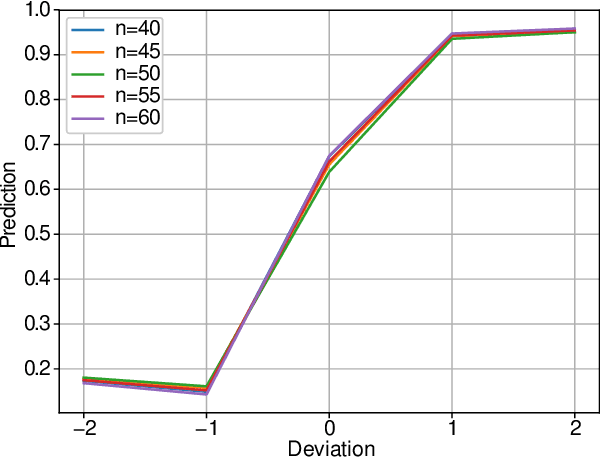
Graph Neural Networks (GNN) are a promising technique for bridging differential programming and combinatorial domains. GNNs employ trainable modules which can be assembled in different configurations that reflect the relational structure of each problem instance. In this paper, we show that GNNs can learn to solve, with very little supervision, the decision variant of the Traveling Salesperson Problem (TSP), a highly relevant $\mathcal{NP}$-Complete problem. Our model is trained to function as an effective message-passing algorithm in which edges (embedded with their weights) communicate with vertices for a number of iterations after which the model is asked to decide whether a route with cost $<C$ exists. We show that such a network can be trained with sets of dual examples: given the optimal tour cost $C^{*}$, we produce one decision instance with target cost $x\%$ smaller and one with target cost $x\%$ larger than $C^{*}$. We were able to obtain $80\%$ accuracy training with $-2\%,+2\%$ deviations, and the same trained model can generalize for more relaxed deviations with increasing performance. We also show that the model is capable of generalizing for larger problem sizes. Finally, we provide a method for predicting the optimal route cost within $2\%$ deviation from the ground truth. In summary, our work shows that Graph Neural Networks are powerful enough to solve $\mathcal{NP}$-Complete problems which combine symbolic and numeric data.

Neural Networks Models for Analyzing Magic: the Gathering Cards

Historically, games of all kinds have often been the subject of study in scientific works of Computer Science, including the field of machine learning. By using machine learning techniques and applying them to a game with defined rules or a structured dataset, it's possible to learn and improve on the already existing techniques and methods to tackle new challenges and solve problems that are out of the ordinary. The already existing work on card games tends to focus on gameplay and card mechanics. This work aims to apply neural networks models, including Convolutional Neural Networks and Recurrent Neural Networks, in order to analyze Magic: the Gathering cards, both in terms of card text and illustrations; the card images and texts are used to train the networks in order to be able to classify them into multiple categories. The ultimate goal was to develop a methodology that could generate card text matching it to an input image, which was attained by relating the prediction values of the images and generated text across the different categories.

Multitask Learning on Graph Neural Networks - Learning Multiple Graph Centrality Measures with a Unified Network

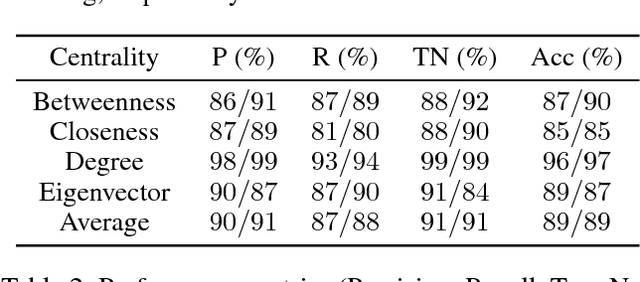
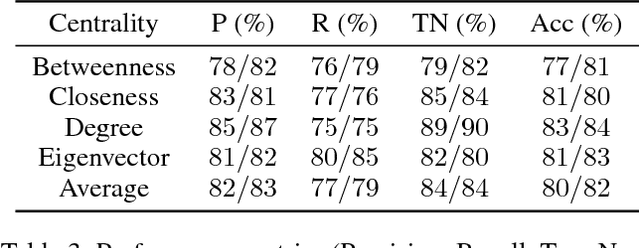
The application of deep learning to symbolic domains remains an active research endeavour. Graph neural networks (GNN), consisting of trained neural modules which can be arranged in different topologies at run time, are sound alternatives to tackle relational problems which lend themselves to graph representations. In this paper, we show that GNNs are capable of multitask learning, which can be naturally enforced by training the model to refine a single set of multidimensional embeddings $\in \mathbb{R}^d$ and decode them into multiple outputs by connecting MLPs at the end of the pipeline. We demonstrate the multitask learning capability of the model in the relevant relational problem of estimating network centrality measures, i.e. is vertex $v_1$ more central than vertex $v_2$ given centrality $c$?. We then show that a GNN can be trained to develop a $lingua$ $franca$ of vertex embeddings from which all relevant information about any of the trained centrality measures can be decoded. The proposed model achieves $89\%$ accuracy on a test dataset of random instances with up to 128 vertices and is shown to generalise to larger problem sizes. The model is also shown to obtain reasonable accuracy on a dataset of real world instances with up to 4k vertices, vastly surpassing the sizes of the largest instances with which the model was trained ($n=128$). Finally, we believe that our contributions attest to the potential of GNNs in symbolic domains in general and in relational learning in particular.