On the Evolution of A.I. and Machine Learning: Towards Measuring and Understanding Impact, Influence, and Leadership at Premier A.I. Conferences

Artificial Intelligence is now recognized as a general-purpose technology with ample impact on human life. In this work, we aim to understand the evolution of AI and Machine learning over the years by analyzing researchers' impact, influence, and leadership over the last decades. This work also intends to shed new light on the history and evolution of AI by exploring the dynamics involved in the field's evolution through the lenses of the papers published on AI conferences since the first International Joint Conference on Artificial Intelligence (IJCAI) in 1969. AI development and evolution have led to increasing research output, reflected in the number of articles published over the last sixty years. We construct comprehensive citation-collaboration and paper-author datasets and compute corresponding centrality measures to carry out our analyses. These analyses allow a better understanding of how AI has reached its current state of affairs in research. Throughout the process, we correlate these datasets with the work of the ACM Turing Award winners and the so-called two AI winters the field has gone through. We also look at self-citation trends and new authors' behaviors. Finally, we present a novel way to infer the country of affiliation of a paper from its organization. Therefore, this work provides a deep analysis of Artificial Intelligence history from information gathered and analyzed from large technical venues datasets and suggests novel insights that can contribute to understanding and measuring AI's evolution.

Neural-Symbolic Relational Reasoning on Graph Models: Effective Link Inference and Computation from Knowledge Bases

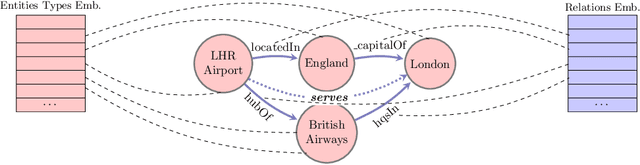
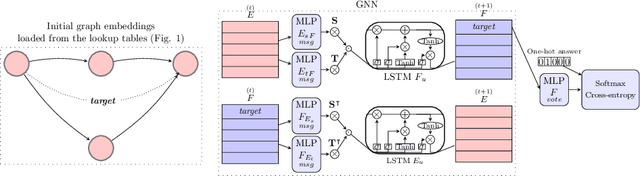
The recent developments and growing interest in neural-symbolic models has shown that hybrid approaches can offer richer models for Artificial Intelligence. The integration of effective relational learning and reasoning methods is one of the key challenges in this direction, as neural learning and symbolic reasoning offer complementary characteristics that can benefit the development of AI systems. Relational labelling or link prediction on knowledge graphs has become one of the main problems in deep learning-based natural language processing research. Moreover, other fields which make use of neural-symbolic techniques may also benefit from such research endeavours. There have been several efforts towards the identification of missing facts from existing ones in knowledge graphs. Two lines of research try and predict knowledge relations between two entities by considering all known facts connecting them or several paths of facts connecting them. We propose a neural-symbolic graph neural network which applies learning over all the paths by feeding the model with the embedding of the minimal subset of the knowledge graph containing such paths. By learning to produce representations for entities and facts corresponding to word embeddings, we show how the model can be trained end-to-end to decode these representations and infer relations between entities in a multitask approach. Our contribution is two-fold: a neural-symbolic methodology leverages the resolution of relational inference in large graphs, and we also demonstrate that such neural-symbolic model is shown more effective than path-based approaches

Graph Colouring Meets Deep Learning: Effective Graph Neural Network Models for Combinatorial Problems

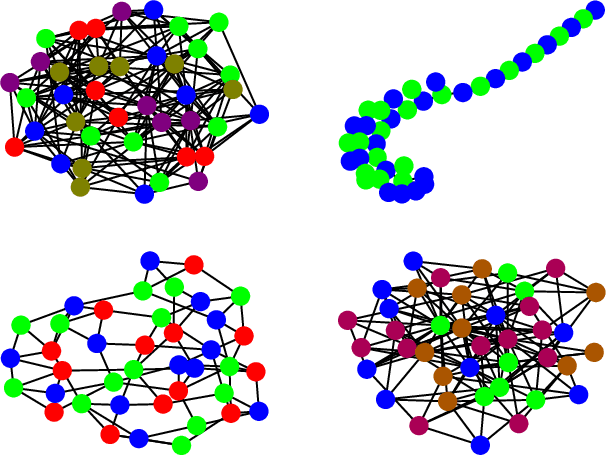
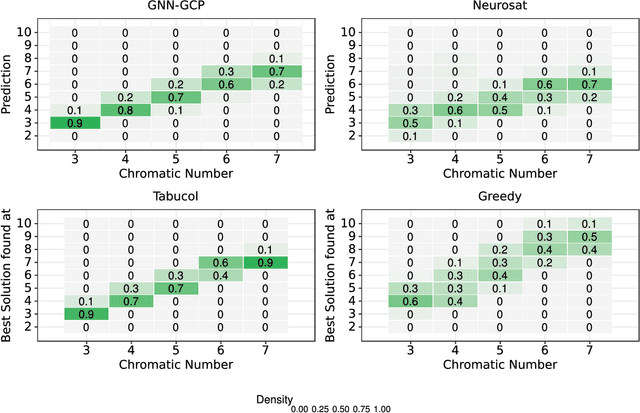
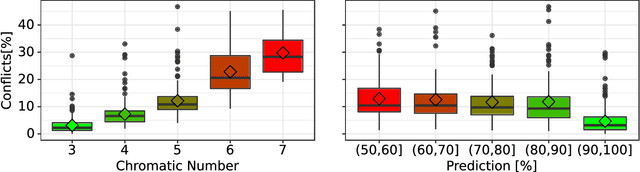
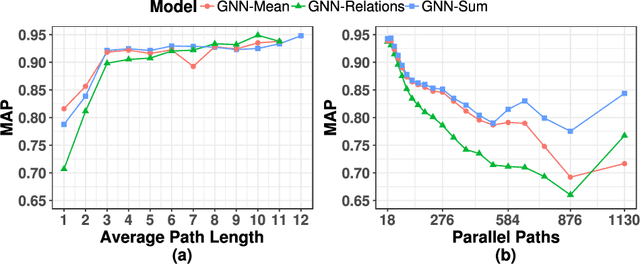
Deep learning has consistently defied state-of-the-art techniques in many fields over the last decade. However, we are just beginning to understand the capabilities of neural learning in symbolic domains. Deep learning architectures that employ parameter sharing over graphs can produce models which can be trained on complex properties of relational data. These include highly relevant NP-Complete problems, such as SAT and TSP. In this work, we showcase how Graph Neural Networks (GNN) can be engineered -- with a very simple architecture -- to solve the fundamental combinatorial problem of graph colouring. Our results show that the model, which achieves high accuracy upon training on random instances, is able to generalise to graph distributions different from those seen at training time. Further, it performs better than the Tabucol and greedy baselines for some distributions. In addition, we show how vertex embeddings can be clustered in multidimensional spaces to yield constructive solutions even though our model is only trained as a binary classifier. In summary, our results contribute to shorten the gap in our understanding of the algorithms learned by GNNs, as well as hoarding empirical evidence for their capability on hard combinatorial problems. Our results thus contribute to the standing challenge of integrating robust learning and symbolic reasoning in Deep Learning systems.

Typed Graph Networks

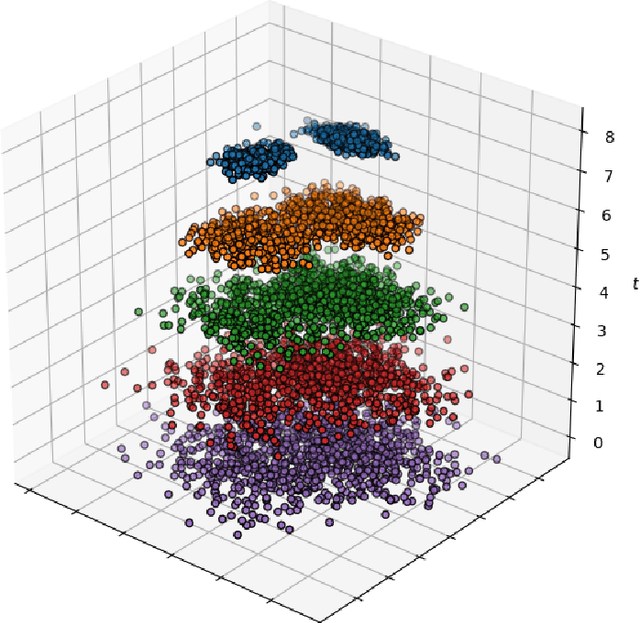
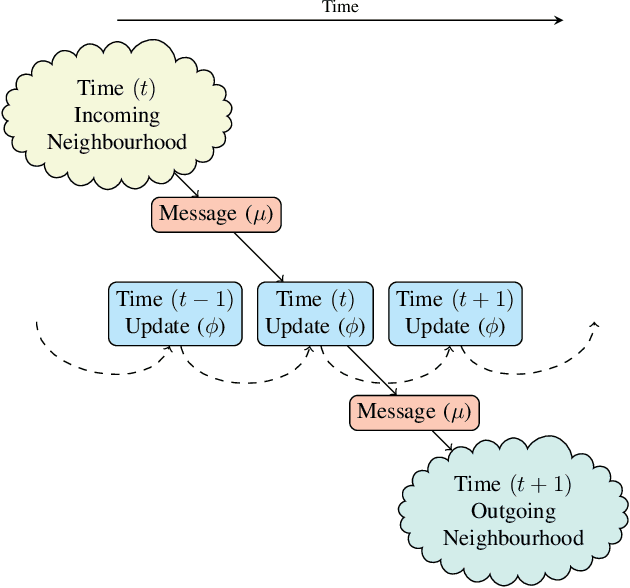
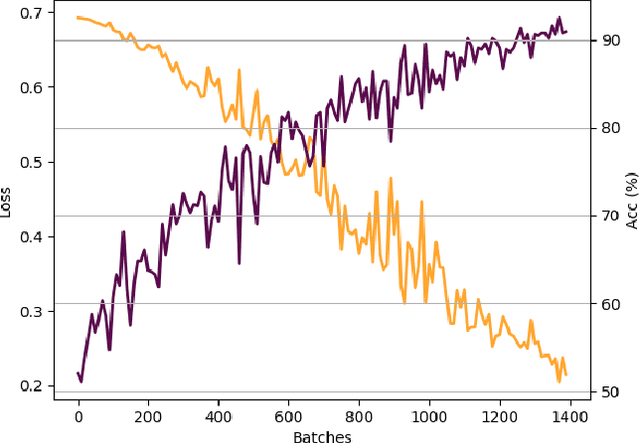
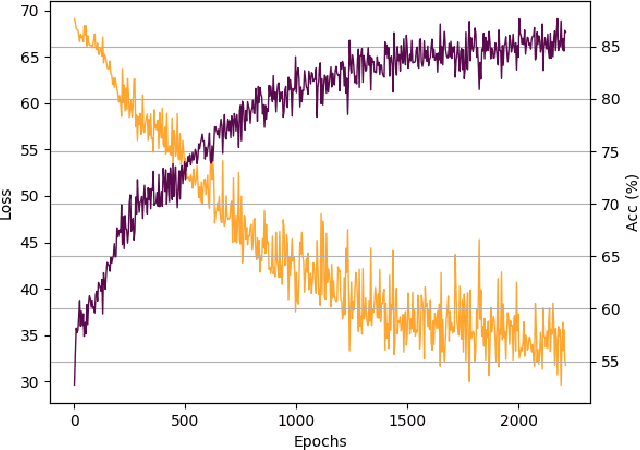
Recently, the deep learning community has given growing attention to neural architectures engineered to learn problems in relational domains. Convolutional Neural Networks employ parameter sharing over the image domain, tying the weights of neural connections on a grid topology and thus enforcing the learning of a number of convolutional kernels. By instantiating trainable neural modules and assembling them in varied configurations (apart from grids), one can enforce parameter sharing over graphs, yielding models which can effectively be fed with relational data. In this context, vertices in a graph can be projected into a hyperdimensional real space and iteratively refined over many message-passing iterations in an end-to-end differentiable architecture. Architectures of this family have been referred to with several definitions in the literature, such as Graph Neural Networks, Message-passing Neural Networks, Relational Networks and Graph Networks. In this paper, we revisit the original Graph Neural Network model and show that it generalises many of the recent models, which in turn benefit from the insight of thinking about vertex \textbf{types}. To illustrate the generality of the original model, we present a Graph Neural Network formalisation, which partitions the vertices of a graph into a number of types. Each type represents an entity in the ontology of the problem one wants to learn. This allows - for instance - one to assign embeddings to edges, hyperedges, and any number of global attributes of the graph. As a companion to this paper we provide a Python/Tensorflow library to facilitate the development of such architectures, with which we instantiate the formalisation to reproduce a number of models proposed in the current literature.

Learning to Solve NP-Complete Problems - A Graph Neural Network for the Decision TSP

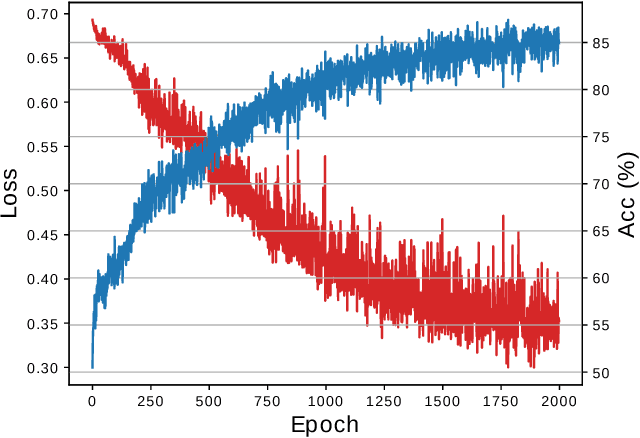
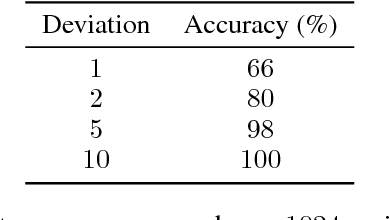
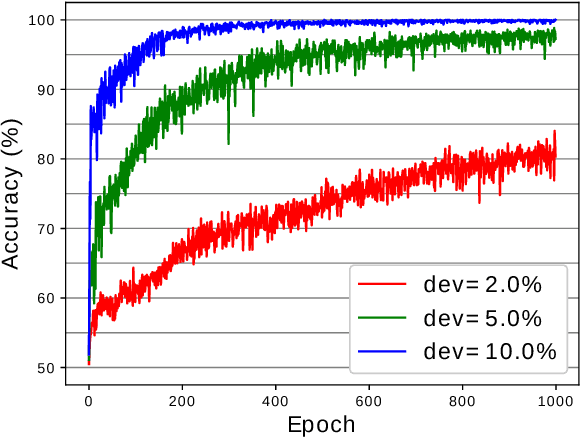
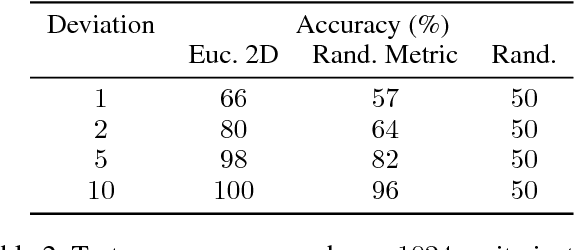
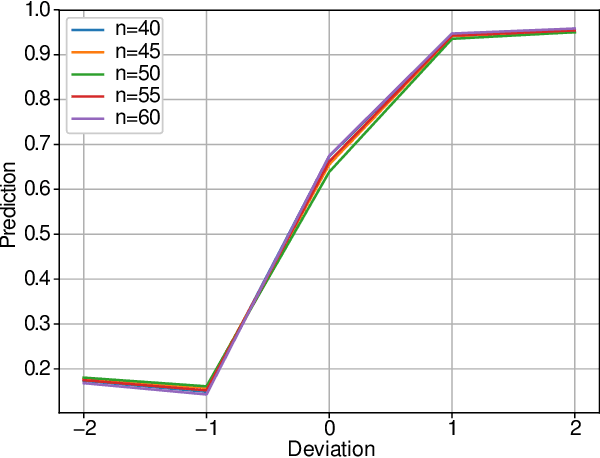
Graph Neural Networks (GNN) are a promising technique for bridging differential programming and combinatorial domains. GNNs employ trainable modules which can be assembled in different configurations that reflect the relational structure of each problem instance. In this paper, we show that GNNs can learn to solve, with very little supervision, the decision variant of the Traveling Salesperson Problem (TSP), a highly relevant $\mathcal{NP}$-Complete problem. Our model is trained to function as an effective message-passing algorithm in which edges (embedded with their weights) communicate with vertices for a number of iterations after which the model is asked to decide whether a route with cost $<C$ exists. We show that such a network can be trained with sets of dual examples: given the optimal tour cost $C^{*}$, we produce one decision instance with target cost $x\%$ smaller and one with target cost $x\%$ larger than $C^{*}$. We were able to obtain $80\%$ accuracy training with $-2\%,+2\%$ deviations, and the same trained model can generalize for more relaxed deviations with increasing performance. We also show that the model is capable of generalizing for larger problem sizes. Finally, we provide a method for predicting the optimal route cost within $2\%$ deviation from the ground truth. In summary, our work shows that Graph Neural Networks are powerful enough to solve $\mathcal{NP}$-Complete problems which combine symbolic and numeric data.

Multitask Learning on Graph Neural Networks - Learning Multiple Graph Centrality Measures with a Unified Network

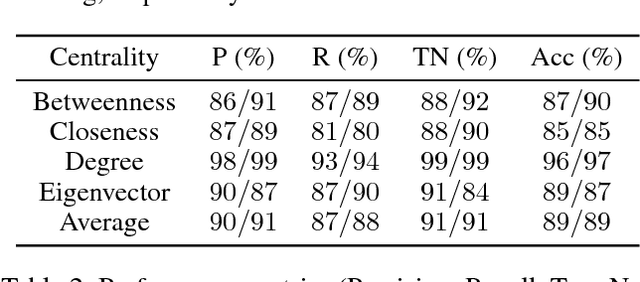
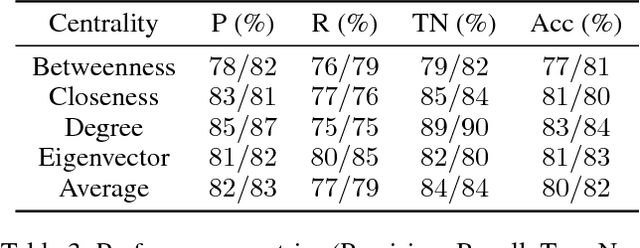
The application of deep learning to symbolic domains remains an active research endeavour. Graph neural networks (GNN), consisting of trained neural modules which can be arranged in different topologies at run time, are sound alternatives to tackle relational problems which lend themselves to graph representations. In this paper, we show that GNNs are capable of multitask learning, which can be naturally enforced by training the model to refine a single set of multidimensional embeddings $\in \mathbb{R}^d$ and decode them into multiple outputs by connecting MLPs at the end of the pipeline. We demonstrate the multitask learning capability of the model in the relevant relational problem of estimating network centrality measures, i.e. is vertex $v_1$ more central than vertex $v_2$ given centrality $c$?. We then show that a GNN can be trained to develop a $lingua$ $franca$ of vertex embeddings from which all relevant information about any of the trained centrality measures can be decoded. The proposed model achieves $89\%$ accuracy on a test dataset of random instances with up to 128 vertices and is shown to generalise to larger problem sizes. The model is also shown to obtain reasonable accuracy on a dataset of real world instances with up to 4k vertices, vastly surpassing the sizes of the largest instances with which the model was trained ($n=128$). Finally, we believe that our contributions attest to the potential of GNNs in symbolic domains in general and in relational learning in particular.