Pedro Avelar
On the Evolution of A.I. and Machine Learning: Towards Measuring and Understanding Impact, Influence, and Leadership at Premier A.I. Conferences
May 26, 2022

Abstract:Artificial Intelligence is now recognized as a general-purpose technology with ample impact on human life. In this work, we aim to understand the evolution of AI and Machine learning over the years by analyzing researchers' impact, influence, and leadership over the last decades. This work also intends to shed new light on the history and evolution of AI by exploring the dynamics involved in the field's evolution through the lenses of the papers published on AI conferences since the first International Joint Conference on Artificial Intelligence (IJCAI) in 1969. AI development and evolution have led to increasing research output, reflected in the number of articles published over the last sixty years. We construct comprehensive citation-collaboration and paper-author datasets and compute corresponding centrality measures to carry out our analyses. These analyses allow a better understanding of how AI has reached its current state of affairs in research. Throughout the process, we correlate these datasets with the work of the ACM Turing Award winners and the so-called two AI winters the field has gone through. We also look at self-citation trends and new authors' behaviors. Finally, we present a novel way to infer the country of affiliation of a paper from its organization. Therefore, this work provides a deep analysis of Artificial Intelligence history from information gathered and analyzed from large technical venues datasets and suggests novel insights that can contribute to understanding and measuring AI's evolution.
Understanding Boolean Function Learnability on Deep Neural Networks
Sep 13, 2020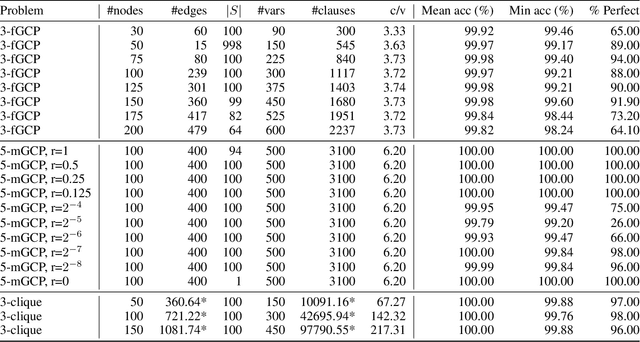
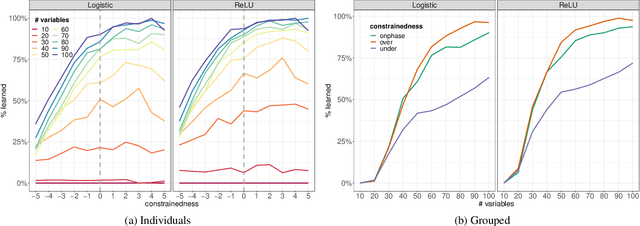
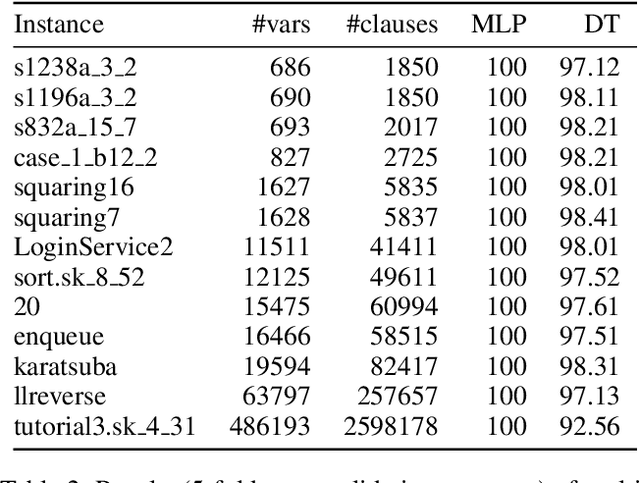
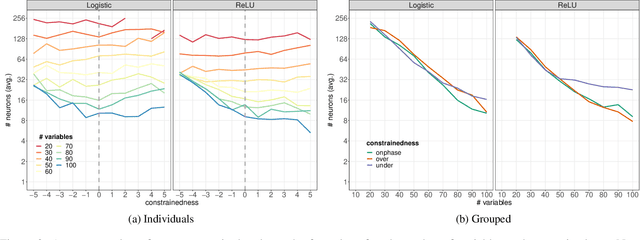
Abstract:Computational learning theory states that many classes of boolean formulas are learnable in polynomial time. This paper addresses the understudied subject of how, in practice, such formulas can be learned by deep neural networks. Specifically, we analyse boolean formulas associated with the decision version of combinatorial optimisation problems, model sampling benchmarks, and random 3-CNFs with varying degrees of constrainedness. Our extensive experiments indicate that: (i) regardless of the combinatorial optimisation problem, relatively small and shallow neural networks are very good approximators of the associated formulas; (ii) smaller formulas seem harder to learn, possibly due to the fewer positive (satisfying) examples available; and (iii) interestingly, underconstrained 3-CNF formulas are more challenging to learn than overconstrained ones. Source code and relevant datasets are publicly available (https://github.com/machine-reasoning-ufrgs/mlbf).
Neural-Symbolic Relational Reasoning on Graph Models: Effective Link Inference and Computation from Knowledge Bases
May 05, 2020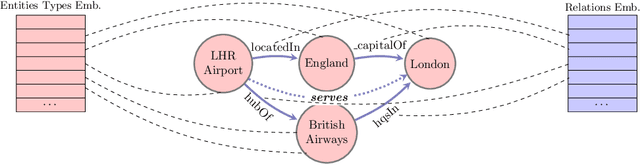

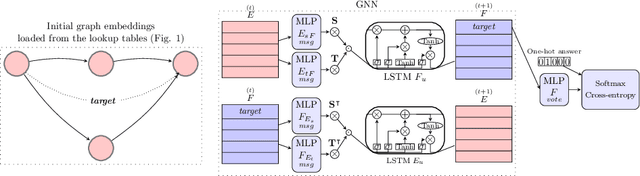
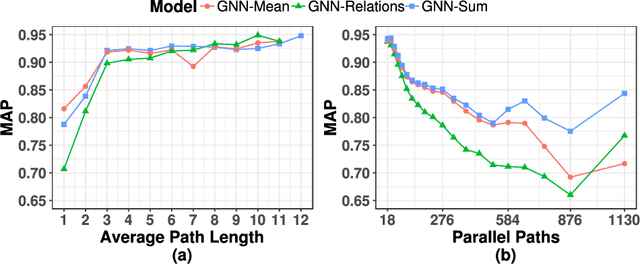
Abstract:The recent developments and growing interest in neural-symbolic models has shown that hybrid approaches can offer richer models for Artificial Intelligence. The integration of effective relational learning and reasoning methods is one of the key challenges in this direction, as neural learning and symbolic reasoning offer complementary characteristics that can benefit the development of AI systems. Relational labelling or link prediction on knowledge graphs has become one of the main problems in deep learning-based natural language processing research. Moreover, other fields which make use of neural-symbolic techniques may also benefit from such research endeavours. There have been several efforts towards the identification of missing facts from existing ones in knowledge graphs. Two lines of research try and predict knowledge relations between two entities by considering all known facts connecting them or several paths of facts connecting them. We propose a neural-symbolic graph neural network which applies learning over all the paths by feeding the model with the embedding of the minimal subset of the knowledge graph containing such paths. By learning to produce representations for entities and facts corresponding to word embeddings, we show how the model can be trained end-to-end to decode these representations and infer relations between entities in a multitask approach. Our contribution is two-fold: a neural-symbolic methodology leverages the resolution of relational inference in large graphs, and we also demonstrate that such neural-symbolic model is shown more effective than path-based approaches
Graph Neural Networks Meet Neural-Symbolic Computing: A Survey and Perspective
Mar 11, 2020
Abstract:Neural-symbolic computing has now become the subject of interest of both academic and industry research laboratories. Graph Neural Networks (GNN) have been widely used in relational and symbolic domains, with widespread application of GNNs in combinatorial optimization, constraint satisfaction, relational reasoning and other scientific domains. The need for improved explainability, interpretability and trust of AI systems in general demands principled methodologies, as suggested by neural-symbolic computing. In this paper, we review the state-of-the-art on the use of GNNs as a model of neural-symbolic computing. This includes the application of GNNs in several domains as well as its relationship to current developments in neural-symbolic computing.
Graph Colouring Meets Deep Learning: Effective Graph Neural Network Models for Combinatorial Problems
Mar 11, 2019
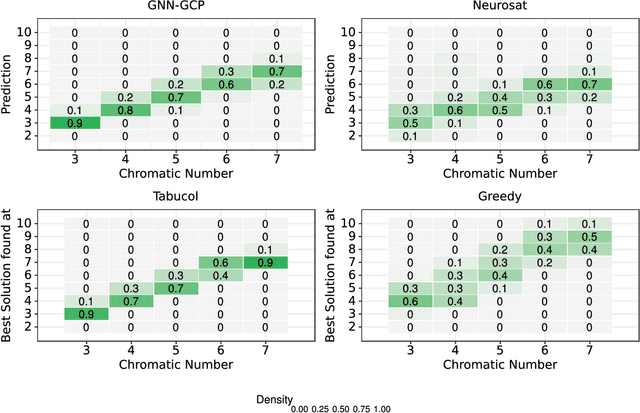
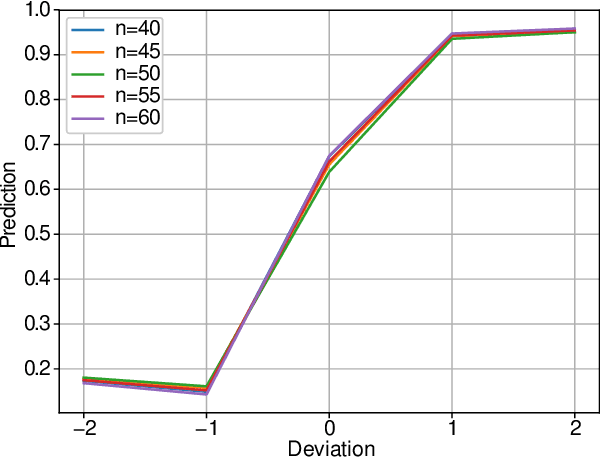
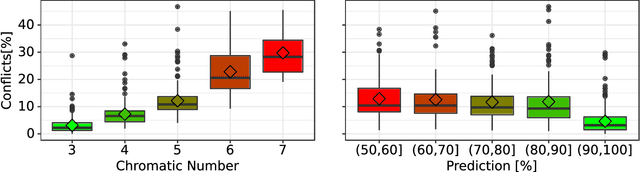
Abstract:Deep learning has consistently defied state-of-the-art techniques in many fields over the last decade. However, we are just beginning to understand the capabilities of neural learning in symbolic domains. Deep learning architectures that employ parameter sharing over graphs can produce models which can be trained on complex properties of relational data. These include highly relevant NP-Complete problems, such as SAT and TSP. In this work, we showcase how Graph Neural Networks (GNN) can be engineered -- with a very simple architecture -- to solve the fundamental combinatorial problem of graph colouring. Our results show that the model, which achieves high accuracy upon training on random instances, is able to generalise to graph distributions different from those seen at training time. Further, it performs better than the Tabucol and greedy baselines for some distributions. In addition, we show how vertex embeddings can be clustered in multidimensional spaces to yield constructive solutions even though our model is only trained as a binary classifier. In summary, our results contribute to shorten the gap in our understanding of the algorithms learned by GNNs, as well as hoarding empirical evidence for their capability on hard combinatorial problems. Our results thus contribute to the standing challenge of integrating robust learning and symbolic reasoning in Deep Learning systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge