Understanding Boolean Function Learnability on Deep Neural Networks
Paper and Code
Sep 13, 2020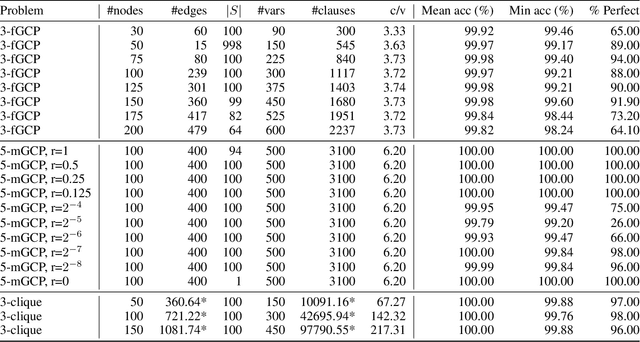
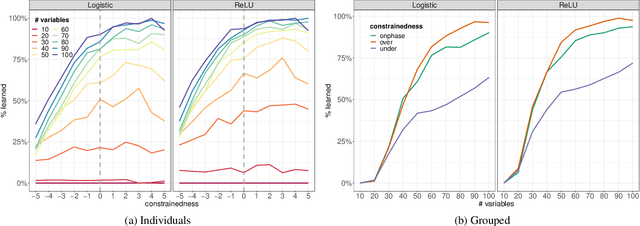
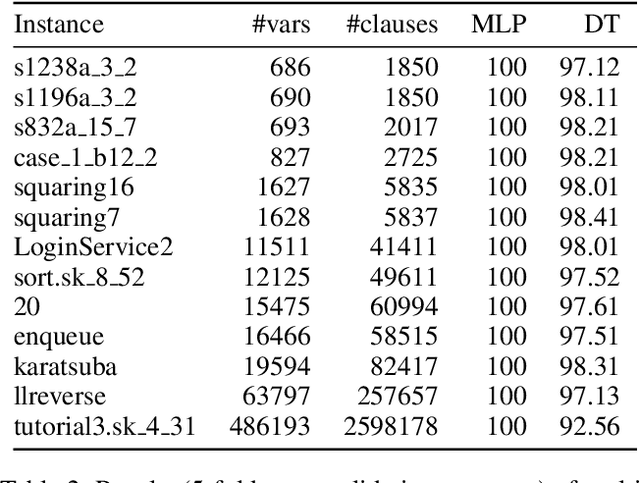
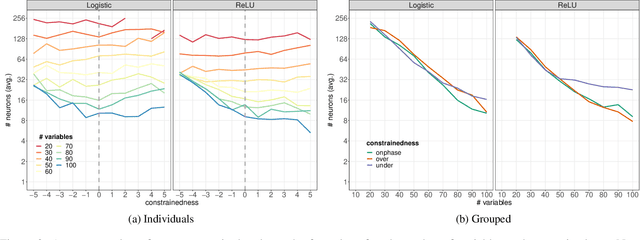
Computational learning theory states that many classes of boolean formulas are learnable in polynomial time. This paper addresses the understudied subject of how, in practice, such formulas can be learned by deep neural networks. Specifically, we analyse boolean formulas associated with the decision version of combinatorial optimisation problems, model sampling benchmarks, and random 3-CNFs with varying degrees of constrainedness. Our extensive experiments indicate that: (i) regardless of the combinatorial optimisation problem, relatively small and shallow neural networks are very good approximators of the associated formulas; (ii) smaller formulas seem harder to learn, possibly due to the fewer positive (satisfying) examples available; and (iii) interestingly, underconstrained 3-CNF formulas are more challenging to learn than overconstrained ones. Source code and relevant datasets are publicly available (https://github.com/machine-reasoning-ufrgs/mlbf).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge