Solving the Kidney-Exchange Problem via Graph Neural Networks with No Supervision

This paper introduces a new learning-based approach for approximately solving the Kidney-Exchange Problem (KEP), an NP-hard problem on graphs. The problem consists of, given a pool of kidney donors and patients waiting for kidney donations, optimally selecting a set of donations to optimize the quantity and quality of transplants performed while respecting a set of constraints about the arrangement of these donations. The proposed technique consists of two main steps: the first is a Graph Neural Network (GNN) trained without supervision; the second is a deterministic non-learned search heuristic that uses the output of the GNN to find paths and cycles. To allow for comparisons, we also implemented and tested an exact solution method using integer programming, two greedy search heuristics without the machine learning module, and the GNN alone without a heuristic. We analyze and compare the methods and conclude that the learning-based two-stage approach is the best solution quality, outputting approximate solutions on average 1.1 times more valuable than the ones from the deterministic heuristic alone.

A Neural Lambda Calculus: Neurosymbolic AI meets the foundations of computing and functional programming

Over the last decades, deep neural networks based-models became the dominant paradigm in machine learning. Further, the use of artificial neural networks in symbolic learning has been seen as increasingly relevant recently. To study the capabilities of neural networks in the symbolic AI domain, researchers have explored the ability of deep neural networks to learn mathematical constructions, such as addition and multiplication, logic inference, such as theorem provers, and even the execution of computer programs. The latter is known to be too complex a task for neural networks. Therefore, the results were not always successful, and often required the introduction of biased elements in the learning process, in addition to restricting the scope of possible programs to be executed. In this work, we will analyze the ability of neural networks to learn how to execute programs as a whole. To do so, we propose a different approach. Instead of using an imperative programming language, with complex structures, we use the Lambda Calculus ({\lambda}-Calculus), a simple, but Turing-Complete mathematical formalism, which serves as the basis for modern functional programming languages and is at the heart of computability theory. We will introduce the use of integrated neural learning and lambda calculi formalization. Finally, we explore execution of a program in {\lambda}-Calculus is based on reductions, we will show that it is enough to learn how to perform these reductions so that we can execute any program. Keywords: Machine Learning, Lambda Calculus, Neurosymbolic AI, Neural Networks, Transformer Model, Sequence-to-Sequence Models, Computational Models

Graph-based Neural Modules to Inspect Attention-based Architectures: A Position Paper

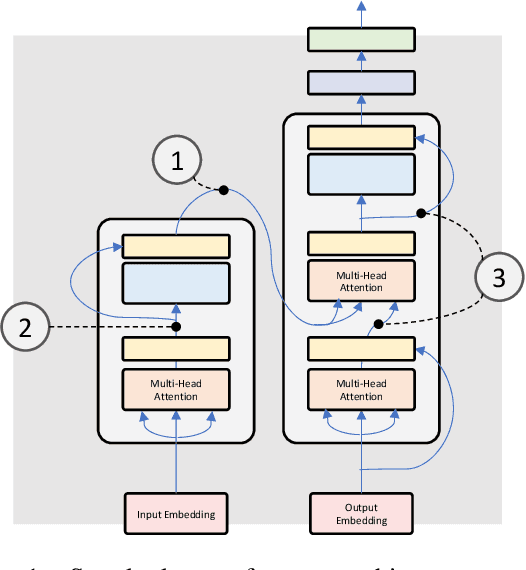
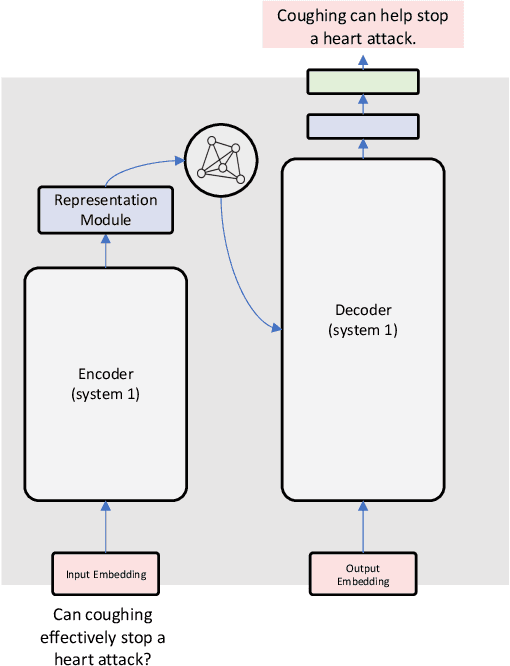
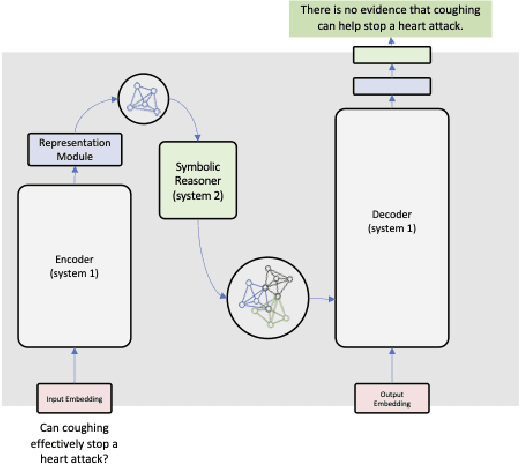
Encoder-decoder architectures are prominent building blocks of state-of-the-art solutions for tasks across multiple fields where deep learning (DL) or foundation models play a key role. Although there is a growing community working on the provision of interpretation for DL models as well as considerable work in the neuro-symbolic community seeking to integrate symbolic representations and DL, many open questions remain around the need for better tools for visualization of the inner workings of DL architectures. In particular, encoder-decoder models offer an exciting opportunity for visualization and editing by humans of the knowledge implicitly represented in model weights. In this work, we explore ways to create an abstraction for segments of the network as a two-way graph-based representation. Changes to this graph structure should be reflected directly in the underlying tensor representations. Such two-way graph representation enables new neuro-symbolic systems by leveraging the pattern recognition capabilities of the encoder-decoder along with symbolic reasoning carried out on the graphs. The approach is expected to produce new ways of interacting with DL models but also to improve performance as a result of the combination of learning and reasoning capabilities.

Neurosymbolic AI: The 3rd Wave

Current advances in Artificial Intelligence (AI) and Machine Learning (ML) have achieved unprecedented impact across research communities and industry. Nevertheless, concerns about trust, safety, interpretability and accountability of AI were raised by influential thinkers. Many have identified the need for well-founded knowledge representation and reasoning to be integrated with deep learning and for sound explainability. Neural-symbolic computing has been an active area of research for many years seeking to bring together robust learning in neural networks with reasoning and explainability via symbolic representations for network models. In this paper, we relate recent and early research results in neurosymbolic AI with the objective of identifying the key ingredients of the next wave of AI systems. We focus on research that integrates in a principled way neural network-based learning with symbolic knowledge representation and logical reasoning. The insights provided by 20 years of neural-symbolic computing are shown to shed new light onto the increasingly prominent role of trust, safety, interpretability and accountability of AI. We also identify promising directions and challenges for the next decade of AI research from the perspective of neural-symbolic systems.

Understanding Boolean Function Learnability on Deep Neural Networks

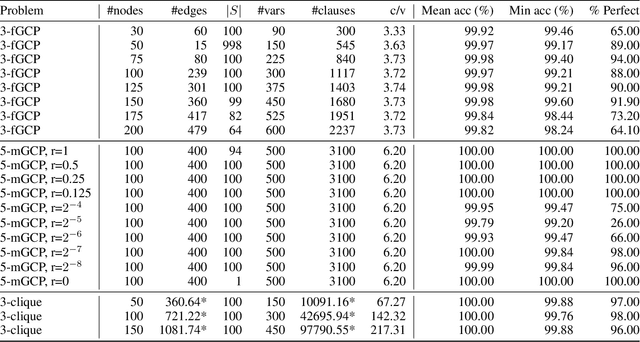
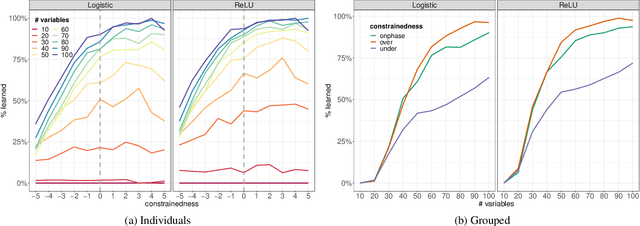
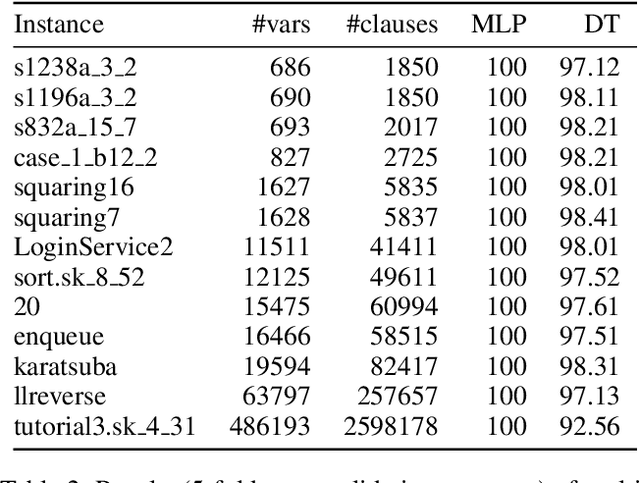
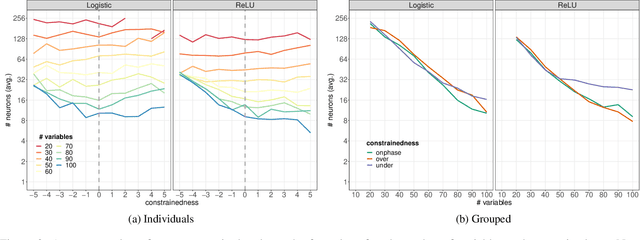
Computational learning theory states that many classes of boolean formulas are learnable in polynomial time. This paper addresses the understudied subject of how, in practice, such formulas can be learned by deep neural networks. Specifically, we analyse boolean formulas associated with the decision version of combinatorial optimisation problems, model sampling benchmarks, and random 3-CNFs with varying degrees of constrainedness. Our extensive experiments indicate that: (i) regardless of the combinatorial optimisation problem, relatively small and shallow neural networks are very good approximators of the associated formulas; (ii) smaller formulas seem harder to learn, possibly due to the fewer positive (satisfying) examples available; and (iii) interestingly, underconstrained 3-CNF formulas are more challenging to learn than overconstrained ones. Source code and relevant datasets are publicly available (https://github.com/machine-reasoning-ufrgs/mlbf).

Discrete and Continuous Deep Residual Learning Over Graphs

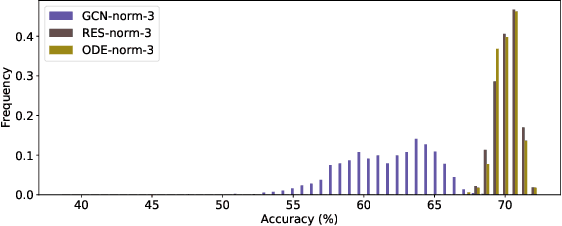
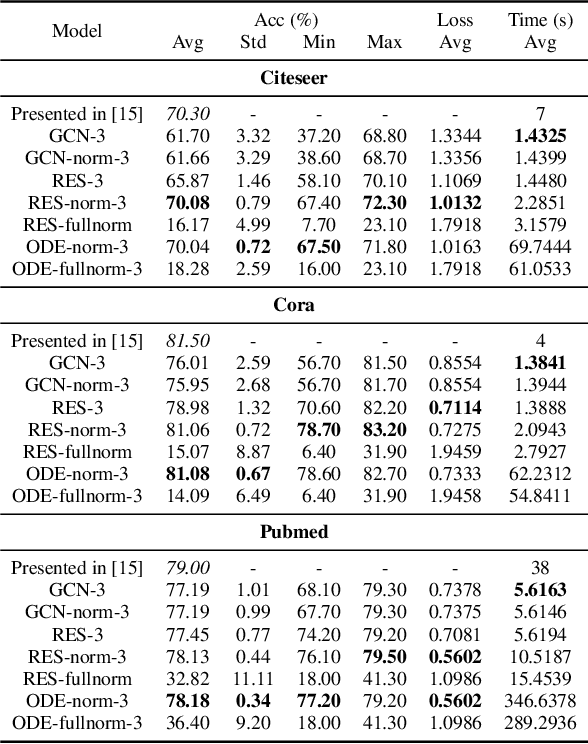
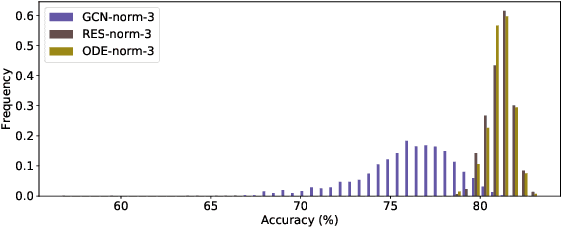
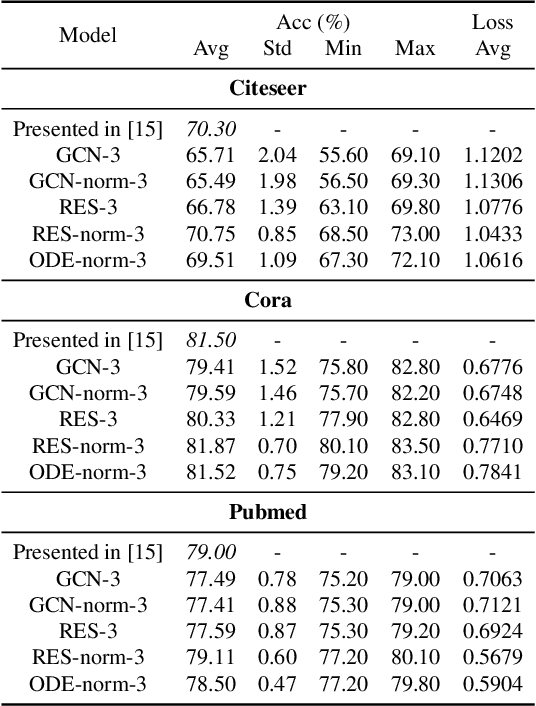
In this paper we propose the use of continuous residual modules for graph kernels in Graph Neural Networks. We show how both discrete and continuous residual layers allow for more robust training, being that continuous residual layers are those which are applied by integrating through an Ordinary Differential Equation (ODE) solver to produce their output. We experimentally show that these residuals achieve better results than the ones with non-residual modules when multiple layers are used, mitigating the low-pass filtering effect of GCN-based models. Finally, we apply and analyse the behaviour of these techniques and give pointers to how this technique can be useful in other domains by allowing more predictable behaviour under dynamic times of computation.

Neural-Symbolic Computing: An Effective Methodology for Principled Integration of Machine Learning and Reasoning

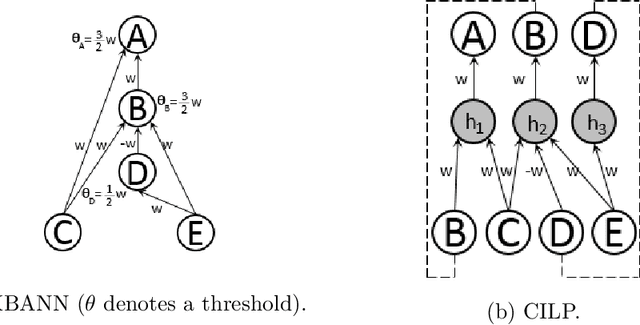
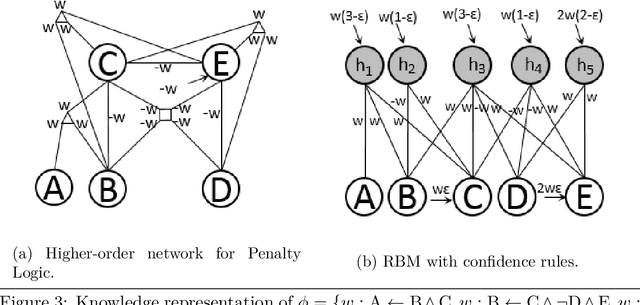
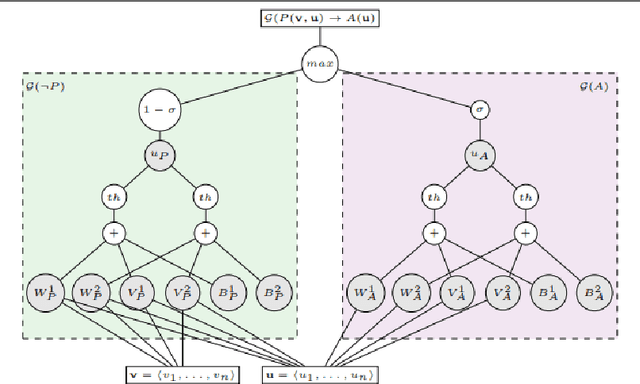
Current advances in Artificial Intelligence and machine learning in general, and deep learning in particular have reached unprecedented impact not only across research communities, but also over popular media channels. However, concerns about interpretability and accountability of AI have been raised by influential thinkers. In spite of the recent impact of AI, several works have identified the need for principled knowledge representation and reasoning mechanisms integrated with deep learning-based systems to provide sound and explainable models for such systems. Neural-symbolic computing aims at integrating, as foreseen by Valiant, two most fundamental cognitive abilities: the ability to learn from the environment, and the ability to reason from what has been learned. Neural-symbolic computing has been an active topic of research for many years, reconciling the advantages of robust learning in neural networks and reasoning and interpretability of symbolic representation. In this paper, we survey recent accomplishments of neural-symbolic computing as a principled methodology for integrated machine learning and reasoning. We illustrate the effectiveness of the approach by outlining the main characteristics of the methodology: principled integration of neural learning with symbolic knowledge representation and reasoning allowing for the construction of explainable AI systems. The insights provided by neural-symbolic computing shed new light on the increasingly prominent need for interpretable and accountable AI systems.

Machine Learning in Network Centrality Measures: Tutorial and Outlook

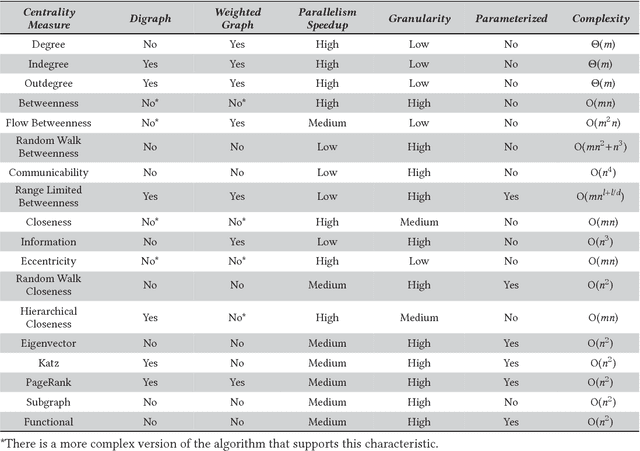
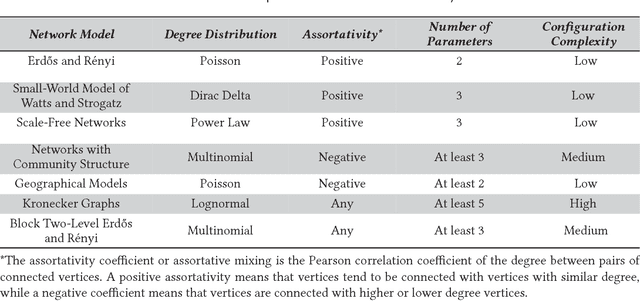
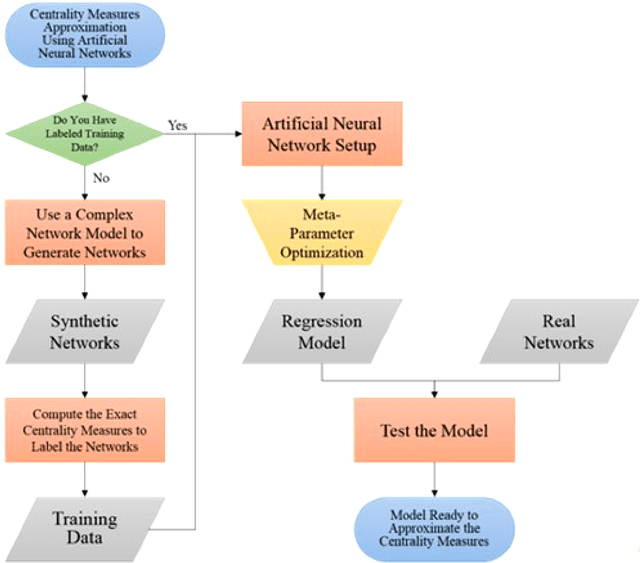
Complex networks are ubiquitous to several Computer Science domains. Centrality measures are an important analysis mechanism to uncover vital elements of complex networks. However, these metrics have high computational costs and requirements that hinder their applications in large real-world networks. In this tutorial, we explain how the use of neural network learning algorithms can render the application of the metrics in complex networks of arbitrary size. Moreover, the tutorial describes how to identify the best configuration for neural network training and learning such for tasks, besides presenting an easy way to generate and acquire training data. We do so by means of a general methodology, using complex network models adaptable to any application. We show that a regression model generated by the neural network successfully approximates the metric values and therefore are a robust, effective alternative in real-world applications. The methodology and proposed machine learning model use only a fraction of time with respect to other approximation algorithms, which is crucial in complex network applications.

Neural-Symbolic Learning and Reasoning: A Survey and Interpretation

The study and understanding of human behaviour is relevant to computer science, artificial intelligence, neural computation, cognitive science, philosophy, psychology, and several other areas. Presupposing cognition as basis of behaviour, among the most prominent tools in the modelling of behaviour are computational-logic systems, connectionist models of cognition, and models of uncertainty. Recent studies in cognitive science, artificial intelligence, and psychology have produced a number of cognitive models of reasoning, learning, and language that are underpinned by computation. In addition, efforts in computer science research have led to the development of cognitive computational systems integrating machine learning and automated reasoning. Such systems have shown promise in a range of applications, including computational biology, fault diagnosis, training and assessment in simulators, and software verification. This joint survey reviews the personal ideas and views of several researchers on neural-symbolic learning and reasoning. The article is organised in three parts: Firstly, we frame the scope and goals of neural-symbolic computation and have a look at the theoretical foundations. We then proceed to describe the realisations of neural-symbolic computation, systems, and applications. Finally we present the challenges facing the area and avenues for further research.