Aligning Generalisation Between Humans and Machines

Recent advances in AI -- including generative approaches -- have resulted in technology that can support humans in scientific discovery and decision support but may also disrupt democracies and target individuals. The responsible use of AI increasingly shows the need for human-AI teaming, necessitating effective interaction between humans and machines. A crucial yet often overlooked aspect of these interactions is the different ways in which humans and machines generalise. In cognitive science, human generalisation commonly involves abstraction and concept learning. In contrast, AI generalisation encompasses out-of-domain generalisation in machine learning, rule-based reasoning in symbolic AI, and abstraction in neuro-symbolic AI. In this perspective paper, we combine insights from AI and cognitive science to identify key commonalities and differences across three dimensions: notions of generalisation, methods for generalisation, and evaluation of generalisation. We map the different conceptualisations of generalisation in AI and cognitive science along these three dimensions and consider their role in human-AI teaming. This results in interdisciplinary challenges across AI and cognitive science that must be tackled to provide a foundation for effective and cognitively supported alignment in human-AI teaming scenarios.

LTNtorch: PyTorch Implementation of Logic Tensor Networks

Logic Tensor Networks (LTN) is a Neuro-Symbolic framework that effectively incorporates deep learning and logical reasoning. In particular, LTN allows defining a logical knowledge base and using it as the objective of a neural model. This makes learning by logical reasoning possible as the parameters of the model are optimized by minimizing a loss function composed of a set of logical formulas expressing facts about the learning task. The framework learns via gradient-descent optimization. Fuzzy logic, a relaxation of classical logic permitting continuous truth values in the interval [0,1], makes this learning possible. Specifically, the training of an LTN consists of three steps. Firstly, (1) the training data is used to ground the formulas. Then, (2) the formulas are evaluated, and the loss function is computed. Lastly, (3) the gradients are back-propagated through the logical computational graph, and the weights of the neural model are changed so the knowledge base is maximally satisfied. LTNtorch is the fully documented and tested PyTorch implementation of Logic Tensor Networks. This paper presents the formalization of LTN and how LTNtorch implements it. Moreover, it provides a basic binary classification example.

IFH: a Diffusion Framework for Flexible Design of Graph Generative Models

Graph generative models can be classified into two prominent families: one-shot models, which generate a graph in one go, and sequential models, which generate a graph by successive additions of nodes and edges. Ideally, between these two extreme models lies a continuous range of models that adopt different levels of sequentiality. This paper proposes a graph generative model, called Insert-Fill-Halt (IFH), that supports the specification of a sequentiality degree. IFH is based upon the theory of Denoising Diffusion Probabilistic Models (DDPM), designing a node removal process that gradually destroys a graph. An insertion process learns to reverse this removal process by inserting arcs and nodes according to the specified sequentiality degree. We evaluate the performance of IFH in terms of quality, run time, and memory, depending on different sequentiality degrees. We also show that using DiGress, a diffusion-based one-shot model, as a generative step in IFH leads to improvement to the model itself, and is competitive with the current state-of-the-art.

Simple and Effective Transfer Learning for Neuro-Symbolic Integration

Deep Learning (DL) techniques have achieved remarkable successes in recent years. However, their ability to generalize and execute reasoning tasks remains a challenge. A potential solution to this issue is Neuro-Symbolic Integration (NeSy), where neural approaches are combined with symbolic reasoning. Most of these methods exploit a neural network to map perceptions to symbols and a logical reasoner to predict the output of the downstream task. These methods exhibit superior generalization capacity compared to fully neural architectures. However, they suffer from several issues, including slow convergence, learning difficulties with complex perception tasks, and convergence to local minima. This paper proposes a simple yet effective method to ameliorate these problems. The key idea involves pretraining a neural model on the downstream task. Then, a NeSy model is trained on the same task via transfer learning, where the weights of the perceptual part are injected from the pretrained network. The key observation of our work is that the neural network fails to generalize only at the level of the symbolic part while being perfectly capable of learning the mapping from perceptions to symbols. We have tested our training strategy on various SOTA NeSy methods and datasets, demonstrating consistent improvements in the aforementioned problems.

Lifted Inference beyond First-Order Logic

Weighted First Order Model Counting (WFOMC) is fundamental to probabilistic inference in statistical relational learning models. As WFOMC is known to be intractable in general ($\#$P-complete), logical fragments that admit polynomial time WFOMC are of significant interest. Such fragments are called domain liftable. Recent works have shown that the two-variable fragment of first order logic extended with counting quantifiers ($\mathrm{C^2}$) is domain-liftable. However, many properties of real-world data, like acyclicity in citation networks and connectivity in social networks, cannot be modeled in $\mathrm{C^2}$, or first order logic in general. In this work, we expand the domain liftability of $\mathrm{C^2}$ with multiple such properties. We show that any $\mathrm{C^2}$ sentence remains domain liftable when one of its relations is restricted to represent a directed acyclic graph, a connected graph, a tree (resp. a directed tree) or a forest (resp. a directed forest). All our results rely on a novel and general methodology of "counting by splitting". Besides their application to probabilistic inference, our results provide a general framework for counting combinatorial structures. We expand a vast array of previous results in discrete mathematics literature on directed acyclic graphs, phylogenetic networks, etc.

logLTN: Differentiable Fuzzy Logic in the Logarithm Space

The AI community is increasingly focused on merging logic with deep learning to create Neuro-Symbolic (NeSy) paradigms and assist neural approaches with symbolic knowledge. A significant trend in the literature involves integrating axioms and facts in loss functions by grounding logical symbols with neural networks and operators with fuzzy semantics. Logic Tensor Networks (LTN) is one of the main representatives in this category, known for its simplicity, efficiency, and versatility. However, it has been previously shown that not all fuzzy operators perform equally when applied in a differentiable setting. Researchers have proposed several configurations of operators, trading off between effectiveness, numerical stability, and generalization to different formulas. This paper presents a configuration of fuzzy operators for grounding formulas end-to-end in the logarithm space. Our goal is to develop a configuration that is more effective than previous proposals, able to handle any formula, and numerically stable. To achieve this, we propose semantics that are best suited for the logarithm space and introduce novel simplifications and improvements that are crucial for optimization via gradient-descent. We use LTN as the framework for our experiments, but the conclusions of our work apply to any similar NeSy framework. Our findings, both formal and empirical, show that the proposed configuration outperforms the state-of-the-art and that each of our modifications is essential in achieving these results.

Weakly-Supervised Visual-Textual Grounding with Semantic Prior Refinement

Using only image-sentence pairs, weakly-supervised visual-textual grounding aims to learn region-phrase correspondences of the respective entity mentions. Compared to the supervised approach, learning is more difficult since bounding boxes and textual phrases correspondences are unavailable. In light of this, we propose the Semantic Prior Refinement Model (SPRM), whose predictions are obtained by combining the output of two main modules. The first untrained module aims to return a rough alignment between textual phrases and bounding boxes. The second trained module is composed of two sub-components that refine the rough alignment to improve the accuracy of the final phrase-bounding box alignments. The model is trained to maximize the multimodal similarity between an image and a sentence, while minimizing the multimodal similarity of the same sentence and a new unrelated image, carefully selected to help the most during training. Our approach shows state-of-the-art results on two popular datasets, Flickr30k Entities and ReferIt, shining especially on ReferIt with a 9.6% absolute improvement. Moreover, thanks to the untrained component, it reaches competitive performances just using a small fraction of training examples.

Interval Logic Tensor Networks

In this paper, we introduce Interval Real Logic (IRL), a two-sorted logic that interprets knowledge such as sequential properties (traces) and event properties using sequences of real-featured data. We interpret connectives using fuzzy logic, event durations using trapezoidal fuzzy intervals, and fuzzy temporal relations using relationships between the intervals' areas. We propose Interval Logic Tensor Networks (ILTN), a neuro-symbolic system that learns by propagating gradients through IRL. In order to support effective learning, ILTN defines smoothened versions of the fuzzy intervals and temporal relations of IRL using softplus activations. We show that ILTN can successfully leverage knowledge expressed in IRL in synthetic tasks that require reasoning about events to predict their fuzzy durations. Our results show that the system is capable of making events compliant with background temporal knowledge.

Weighted First Order Model Counting with Directed Acyclic Graph Axioms

Weighted First Order Model Counting (WFOMC) is the task of computing the weighted sum of the models of a first-order logic sentence. Probabilistic inference problems in many statistical relational learning frameworks can be cast as a WFOMC problem. However, in general, WFOMC is known to be intractable (#P_1- complete). Hence, logical fragments that admit polynomial time WFOMC are of significant interest. Such fragments are called domain liftable. Recent works have identified the two-variable fragment of first-order logic, extended with counting quantifiers, to be domain liftable. In this paper, we extend this fragment with a Directed Acyclic Graph axiom, i.e., a relation is interpreted as a Directed Acyclic Graph.

Planning for Learning Object Properties

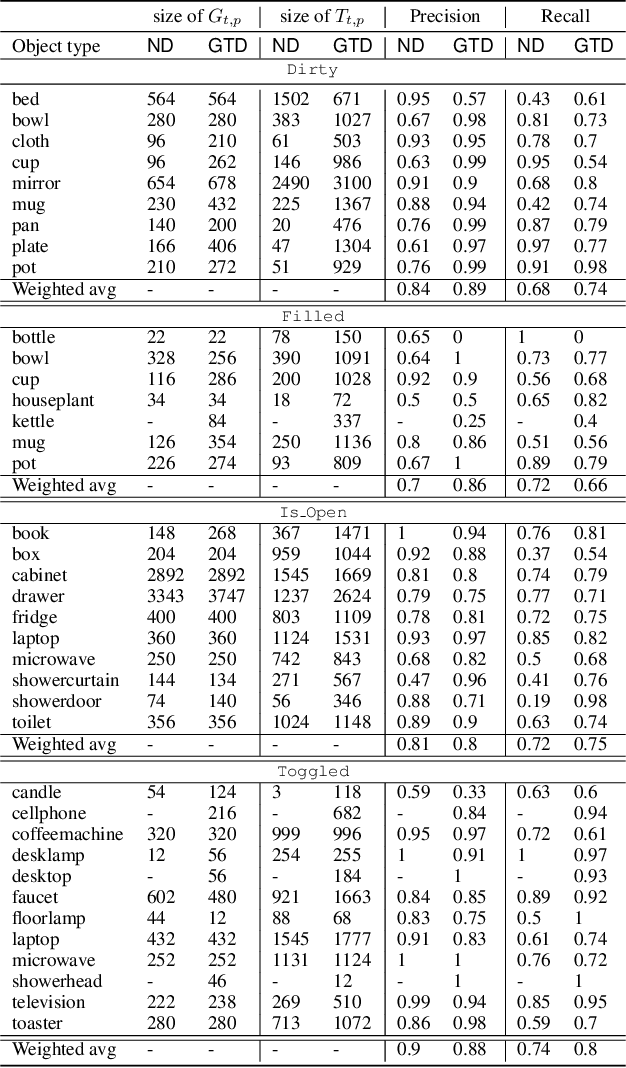
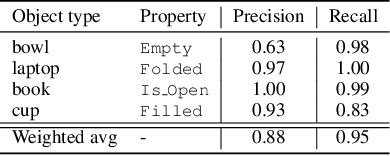
Autonomous agents embedded in a physical environment need the ability to recognize objects and their properties from sensory data. Such a perceptual ability is often implemented by supervised machine learning models, which are pre-trained using a set of labelled data. In real-world, open-ended deployments, however, it is unrealistic to assume to have a pre-trained model for all possible environments. Therefore, agents need to dynamically learn/adapt/extend their perceptual abilities online, in an autonomous way, by exploring and interacting with the environment where they operate. This paper describes a way to do so, by exploiting symbolic planning. Specifically, we formalize the problem of automatically training a neural network to recognize object properties as a symbolic planning problem (using PDDL). We use planning techniques to produce a strategy for automating the training dataset creation and the learning process. Finally, we provide an experimental evaluation in both a simulated and a real environment, which shows that the proposed approach is able to successfully learn how to recognize new object properties.