ULLER: A Unified Language for Learning and Reasoning

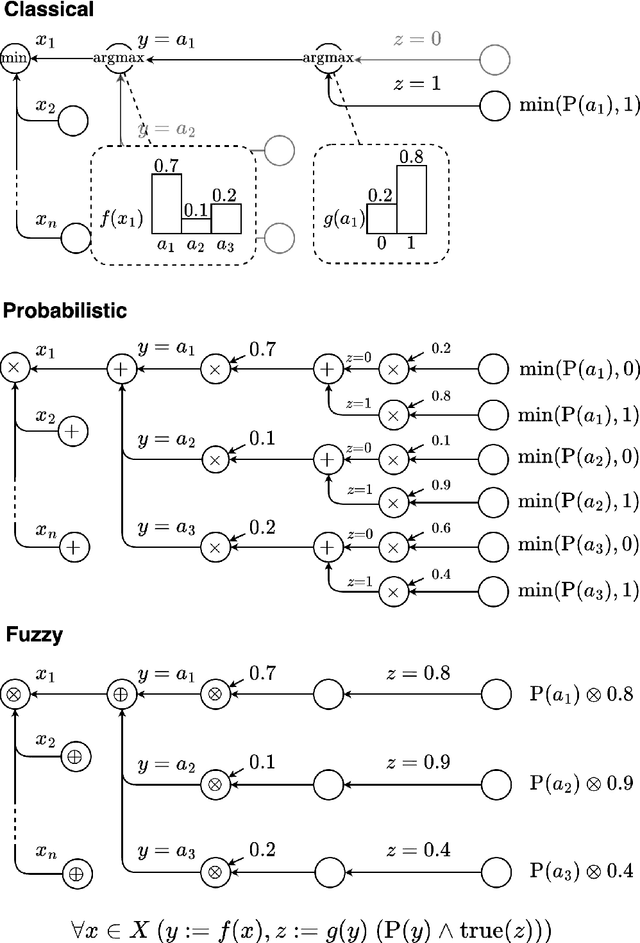
The field of neuro-symbolic artificial intelligence (NeSy), which combines learning and reasoning, has recently experienced significant growth. There now are a wide variety of NeSy frameworks, each with its own specific language for expressing background knowledge and how to relate it to neural networks. This heterogeneity hinders accessibility for newcomers and makes comparing different NeSy frameworks challenging. We propose a unified language for NeSy, which we call ULLER, a Unified Language for LEarning and Reasoning. ULLER encompasses a wide variety of settings, while ensuring that knowledge described in it can be used in existing NeSy systems. ULLER has a neuro-symbolic first-order syntax for which we provide example semantics including classical, fuzzy, and probabilistic logics. We believe ULLER is a first step towards making NeSy research more accessible and comparable, paving the way for libraries that streamline training and evaluation across a multitude of semantics, knowledge bases, and NeSy systems.

logLTN: Differentiable Fuzzy Logic in the Logarithm Space

The AI community is increasingly focused on merging logic with deep learning to create Neuro-Symbolic (NeSy) paradigms and assist neural approaches with symbolic knowledge. A significant trend in the literature involves integrating axioms and facts in loss functions by grounding logical symbols with neural networks and operators with fuzzy semantics. Logic Tensor Networks (LTN) is one of the main representatives in this category, known for its simplicity, efficiency, and versatility. However, it has been previously shown that not all fuzzy operators perform equally when applied in a differentiable setting. Researchers have proposed several configurations of operators, trading off between effectiveness, numerical stability, and generalization to different formulas. This paper presents a configuration of fuzzy operators for grounding formulas end-to-end in the logarithm space. Our goal is to develop a configuration that is more effective than previous proposals, able to handle any formula, and numerically stable. To achieve this, we propose semantics that are best suited for the logarithm space and introduce novel simplifications and improvements that are crucial for optimization via gradient-descent. We use LTN as the framework for our experiments, but the conclusions of our work apply to any similar NeSy framework. Our findings, both formal and empirical, show that the proposed configuration outperforms the state-of-the-art and that each of our modifications is essential in achieving these results.

KitchenScale: Learning to predict ingredient quantities from recipe contexts

Determining proper quantities for ingredients is an essential part of cooking practice from the perspective of enriching tastiness and promoting healthiness. We introduce KitchenScale, a fine-tuned Pre-trained Language Model (PLM) that predicts a target ingredient's quantity and measurement unit given its recipe context. To effectively train our KitchenScale model, we formulate an ingredient quantity prediction task that consists of three sub-tasks which are ingredient measurement type classification, unit classification, and quantity regression task. Furthermore, we utilized transfer learning of cooking knowledge from recipe texts to PLMs. We adopted the Discrete Latent Exponent (DExp) method to cope with high variance of numerical scales in recipe corpora. Experiments with our newly constructed dataset and recommendation examples demonstrate KitchenScale's understanding of various recipe contexts and generalizability in predicting ingredient quantities. We implemented a web application for KitchenScale to demonstrate its functionality in recommending ingredient quantities expressed in numerals (e.g., 2) with units (e.g., ounce).

Interval Logic Tensor Networks

In this paper, we introduce Interval Real Logic (IRL), a two-sorted logic that interprets knowledge such as sequential properties (traces) and event properties using sequences of real-featured data. We interpret connectives using fuzzy logic, event durations using trapezoidal fuzzy intervals, and fuzzy temporal relations using relationships between the intervals' areas. We propose Interval Logic Tensor Networks (ILTN), a neuro-symbolic system that learns by propagating gradients through IRL. In order to support effective learning, ILTN defines smoothened versions of the fuzzy intervals and temporal relations of IRL using softplus activations. We show that ILTN can successfully leverage knowledge expressed in IRL in synthetic tasks that require reasoning about events to predict their fuzzy durations. Our results show that the system is capable of making events compliant with background temporal knowledge.

Logic Tensor Networks

Artificial Intelligence agents are required to learn from their surroundings and to reason about the knowledge that has been learned in order to make decisions. While state-of-the-art learning from data typically uses sub-symbolic distributed representations, reasoning is normally useful at a higher level of abstraction with the use of a first-order logic language for knowledge representation. As a result, attempts at combining symbolic AI and neural computation into neural-symbolic systems have been on the increase. In this paper, we present Logic Tensor Networks (LTN), a neurosymbolic formalism and computational model that supports learning and reasoning through the introduction of a many-valued, end-to-end differentiable first-order logic called Real Logic as a representation language for deep learning. We show that LTN provides a uniform language for the specification and the computation of several AI tasks such as data clustering, multi-label classification, relational learning, query answering, semi-supervised learning, regression and embedding learning. We implement and illustrate each of the above tasks with a number of simple explanatory examples using TensorFlow 2. Keywords: Neurosymbolic AI, Deep Learning and Reasoning, Many-valued Logic.

Injecting Prior Knowledge for Transfer Learning into Reinforcement Learning Algorithms using Logic Tensor Networks

Human ability at solving complex tasks is helped by priors on object and event semantics of their environment. This paper investigates the use of similar prior knowledge for transfer learning in Reinforcement Learning agents. In particular, the paper proposes to use a first-order-logic language grounded in deep neural networks to represent facts about objects and their semantics in the real world. Facts are provided as background knowledge a priori to learning a policy for how to act in the world. The priors are injected with the conventional input in a single agent architecture. As proof-of-concept, the paper tests the system in simple experiments that show the importance of symbolic abstraction and flexible fact derivation. The paper shows that the proposed system can learn to take advantage of both the symbolic layer and the image layer in a single decision selection module.