Robin Manhaeve
ProbLog4Fairness: A Neurosymbolic Approach to Modeling and Mitigating Bias
Nov 12, 2025

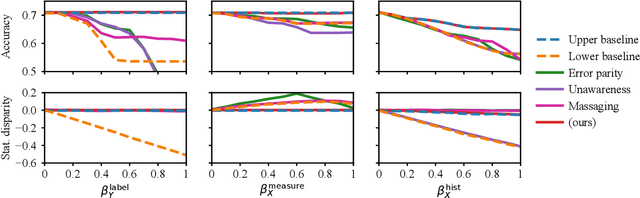

Abstract:Operationalizing definitions of fairness is difficult in practice, as multiple definitions can be incompatible while each being arguably desirable. Instead, it may be easier to directly describe algorithmic bias through ad-hoc assumptions specific to a particular real-world task, e.g., based on background information on systemic biases in its context. Such assumptions can, in turn, be used to mitigate this bias during training. Yet, a framework for incorporating such assumptions that is simultaneously principled, flexible, and interpretable is currently lacking. Our approach is to formalize bias assumptions as programs in ProbLog, a probabilistic logic programming language that allows for the description of probabilistic causal relationships through logic. Neurosymbolic extensions of ProbLog then allow for easy integration of these assumptions in a neural network's training process. We propose a set of templates to express different types of bias and show the versatility of our approach on synthetic tabular datasets with known biases. Using estimates of the bias distortions present, we also succeed in mitigating algorithmic bias in real-world tabular and image data. We conclude that ProbLog4Fairness outperforms baselines due to its ability to flexibly model the relevant bias assumptions, where other methods typically uphold a fixed bias type or notion of fairness.
DeepGraphLog for Layered Neurosymbolic AI
Sep 09, 2025Abstract:Neurosymbolic AI (NeSy) aims to integrate the statistical strengths of neural networks with the interpretability and structure of symbolic reasoning. However, current NeSy frameworks like DeepProbLog enforce a fixed flow where symbolic reasoning always follows neural processing. This restricts their ability to model complex dependencies, especially in irregular data structures such as graphs. In this work, we introduce DeepGraphLog, a novel NeSy framework that extends ProbLog with Graph Neural Predicates. DeepGraphLog enables multi-layer neural-symbolic reasoning, allowing neural and symbolic components to be layered in arbitrary order. In contrast to DeepProbLog, which cannot handle symbolic reasoning via neural methods, DeepGraphLog treats symbolic representations as graphs, enabling them to be processed by Graph Neural Networks (GNNs). We showcase the capabilities of DeepGraphLog on tasks in planning, knowledge graph completion with distant supervision, and GNN expressivity. Our results demonstrate that DeepGraphLog effectively captures complex relational dependencies, overcoming key limitations of existing NeSy systems. By broadening the applicability of neurosymbolic AI to graph-structured domains, DeepGraphLog offers a more expressive and flexible framework for neural-symbolic integration.
Towards a fully declarative neuro-symbolic language
May 15, 2024

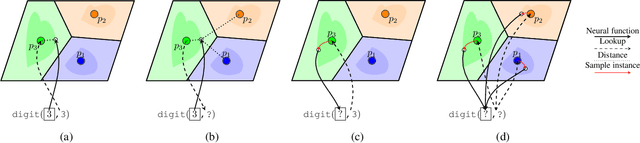
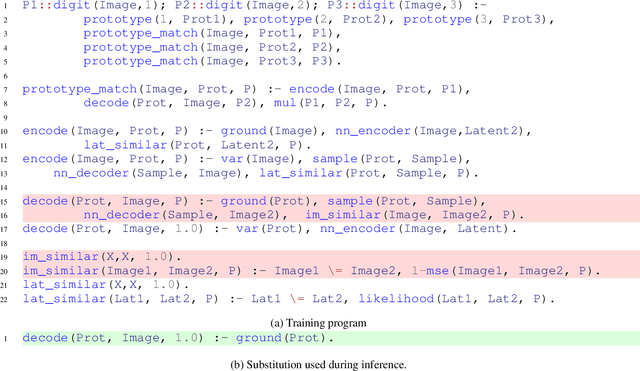
Abstract:Neuro-symbolic systems (NeSy), which claim to combine the best of both learning and reasoning capabilities of artificial intelligence, are missing a core property of reasoning systems: Declarativeness. The lack of declarativeness is caused by the functional nature of neural predicates inherited from neural networks. We propose and implement a general framework for fully declarative neural predicates, which hence extends to fully declarative NeSy frameworks. We first show that the declarative extension preserves the learning and reasoning capabilities while being able to answer arbitrary queries while only being trained on a single query type.
ULLER: A Unified Language for Learning and Reasoning
May 01, 2024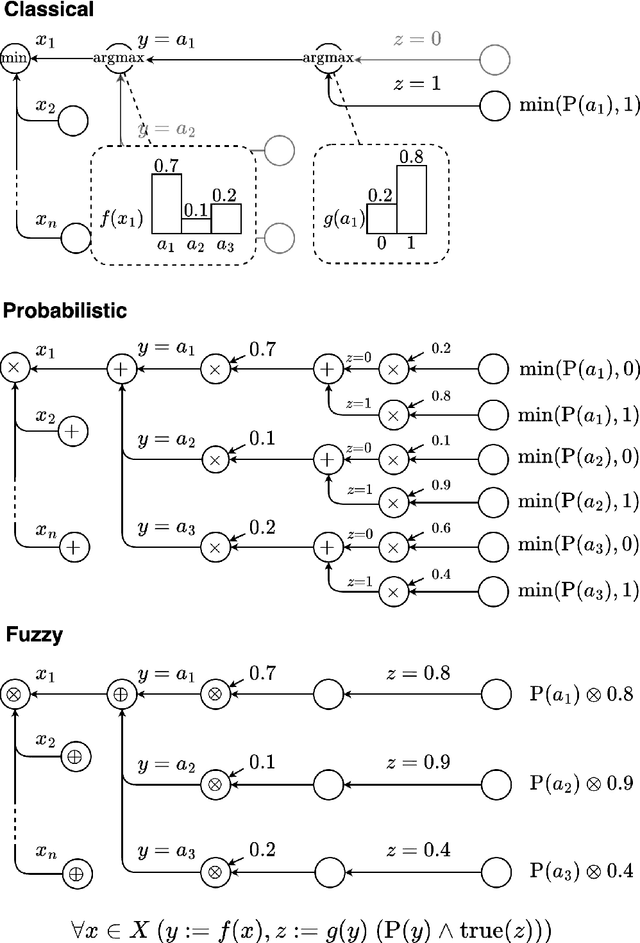
Abstract:The field of neuro-symbolic artificial intelligence (NeSy), which combines learning and reasoning, has recently experienced significant growth. There now are a wide variety of NeSy frameworks, each with its own specific language for expressing background knowledge and how to relate it to neural networks. This heterogeneity hinders accessibility for newcomers and makes comparing different NeSy frameworks challenging. We propose a unified language for NeSy, which we call ULLER, a Unified Language for LEarning and Reasoning. ULLER encompasses a wide variety of settings, while ensuring that knowledge described in it can be used in existing NeSy systems. ULLER has a neuro-symbolic first-order syntax for which we provide example semantics including classical, fuzzy, and probabilistic logics. We believe ULLER is a first step towards making NeSy research more accessible and comparable, paving the way for libraries that streamline training and evaluation across a multitude of semantics, knowledge bases, and NeSy systems.
Semirings for Probabilistic and Neuro-Symbolic Logic Programming
Feb 21, 2024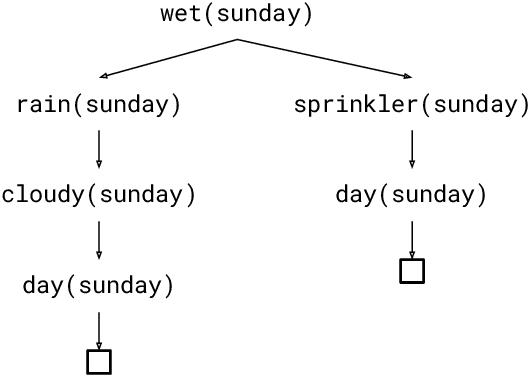

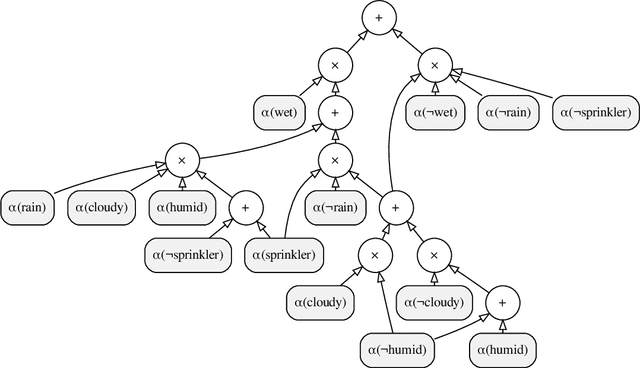
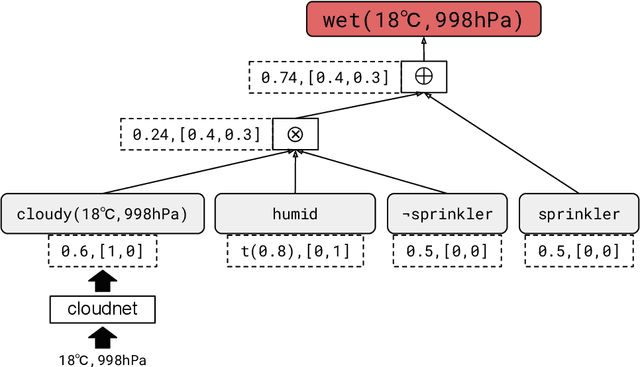
Abstract:The field of probabilistic logic programming (PLP) focuses on integrating probabilistic models into programming languages based on logic. Over the past 30 years, numerous languages and frameworks have been developed for modeling, inference and learning in probabilistic logic programs. While originally PLP focused on discrete probability, more recent approaches have incorporated continuous distributions as well as neural networks, effectively yielding neural-symbolic methods. We provide a unified algebraic perspective on PLP, showing that many if not most of the extensions of PLP can be cast within a common algebraic logic programming framework, in which facts are labeled with elements of a semiring and disjunction and conjunction are replaced by addition and multiplication. This does not only hold for the PLP variations itself but also for the underlying execution mechanism that is based on (algebraic) model counting.
A Bayesian Unification of Self-Supervised Clustering and Energy-Based Models
Dec 30, 2023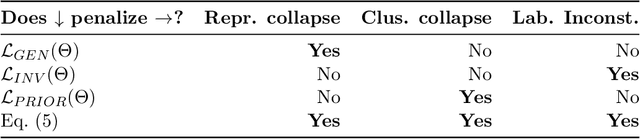
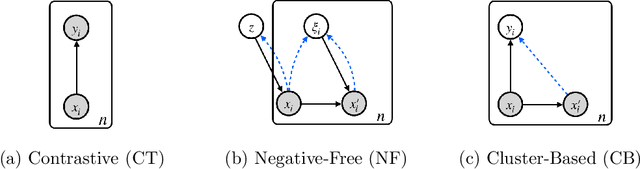
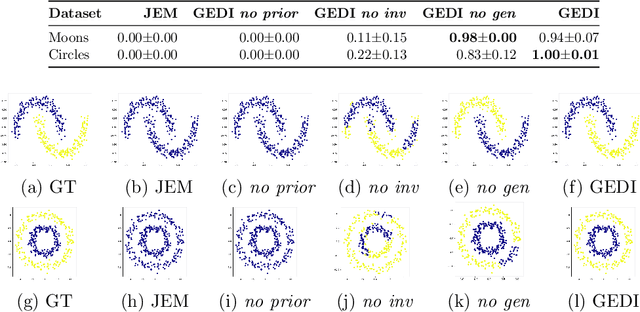
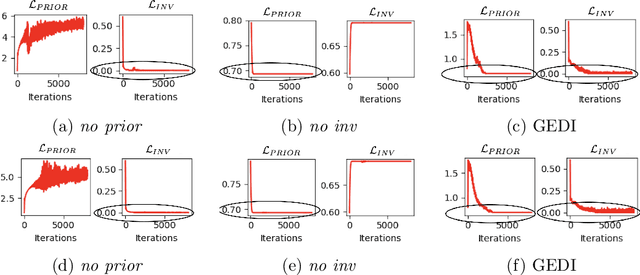
Abstract:Self-supervised learning is a popular and powerful method for utilizing large amounts of unlabeled data, for which a wide variety of training objectives have been proposed in the literature. In this study, we perform a Bayesian analysis of state-of-the-art self-supervised learning objectives, elucidating the underlying probabilistic graphical models in each class and presenting a standardized methodology for their derivation from first principles. The analysis also indicates a natural means of integrating self-supervised learning with likelihood-based generative models. We instantiate this concept within the realm of cluster-based self-supervised learning and energy models, introducing a novel lower bound which is proven to reliably penalize the most important failure modes. Furthermore, this newly proposed lower bound enables the training of a standard backbone architecture without the necessity for asymmetric elements such as stop gradients, momentum encoders, or specialized clustering layers - typically introduced to avoid learning trivial solutions. Our theoretical findings are substantiated through experiments on synthetic and real-world data, including SVHN, CIFAR10, and CIFAR100, thus showing that our objective function allows to outperform existing self-supervised learning strategies in terms of clustering, generation and out-of-distribution detection performance by a wide margin. We also demonstrate that GEDI can be integrated into a neural-symbolic framework to mitigate the reasoning shortcut problem and to learn higher quality symbolic representations thanks to the enhanced classification performance.
Learning Symbolic Representations Through Joint GEnerative and DIscriminative Training
Apr 22, 2023



Abstract:We introduce GEDI, a Bayesian framework that combines existing self-supervised learning objectives with likelihood-based generative models. This framework leverages the benefits of both GEnerative and DIscriminative approaches, resulting in improved symbolic representations over standalone solutions. Additionally, GEDI can be easily integrated and trained jointly with existing neuro-symbolic frameworks without the need for additional supervision or costly pre-training steps. We demonstrate through experiments on real-world data, including SVHN, CIFAR10, and CIFAR100, that GEDI outperforms existing self-supervised learning strategies in terms of clustering performance by a significant margin. The symbolic component further allows it to leverage knowledge in the form of logical constraints to improve performance in the small data regime.
* ICLR 2023 Workshop NeSy-GeMs. arXiv admin note: substantial text overlap with arXiv:2212.13425
Neural Probabilistic Logic Programming in Discrete-Continuous Domains
Mar 14, 2023Abstract:Neural-symbolic AI (NeSy) allows neural networks to exploit symbolic background knowledge in the form of logic. It has been shown to aid learning in the limited data regime and to facilitate inference on out-of-distribution data. Probabilistic NeSy focuses on integrating neural networks with both logic and probability theory, which additionally allows learning under uncertainty. A major limitation of current probabilistic NeSy systems, such as DeepProbLog, is their restriction to finite probability distributions, i.e., discrete random variables. In contrast, deep probabilistic programming (DPP) excels in modelling and optimising continuous probability distributions. Hence, we introduce DeepSeaProbLog, a neural probabilistic logic programming language that incorporates DPP techniques into NeSy. Doing so results in the support of inference and learning of both discrete and continuous probability distributions under logical constraints. Our main contributions are 1) the semantics of DeepSeaProbLog and its corresponding inference algorithm, 2) a proven asymptotically unbiased learning algorithm, and 3) a series of experiments that illustrate the versatility of our approach.
GEDI: GEnerative and DIscriminative Training for Self-Supervised Learning
Dec 29, 2022Abstract:Self-supervised learning is a popular and powerful method for utilizing large amounts of unlabeled data, for which a wide variety of training objectives have been proposed in the literature. In this study, we perform a Bayesian analysis of state-of-the-art self-supervised learning objectives and propose a unified formulation based on likelihood learning. Our analysis suggests a simple method for integrating self-supervised learning with generative models, allowing for the joint training of these two seemingly distinct approaches. We refer to this combined framework as GEDI, which stands for GEnerative and DIscriminative training. Additionally, we demonstrate an instantiation of the GEDI framework by integrating an energy-based model with a cluster-based self-supervised learning model. Through experiments on synthetic and real-world data, including SVHN, CIFAR10, and CIFAR100, we show that GEDI outperforms existing self-supervised learning strategies in terms of clustering performance by a wide margin. We also demonstrate that GEDI can be integrated into a neural-symbolic framework to address tasks in the small data regime, where it can use logical constraints to further improve clustering and classification performance.
From Statistical Relational to Neural Symbolic Artificial Intelligence: a Survey
Aug 25, 2021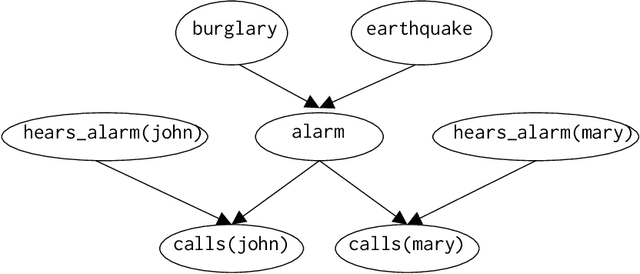
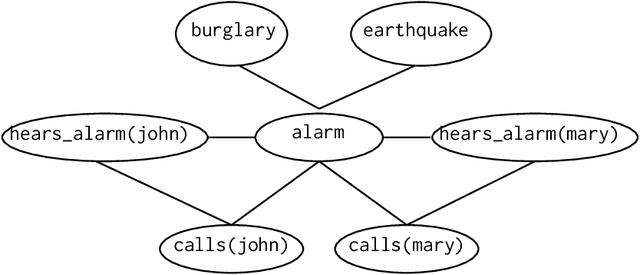
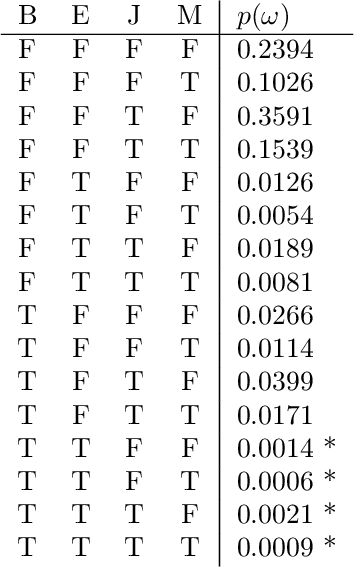
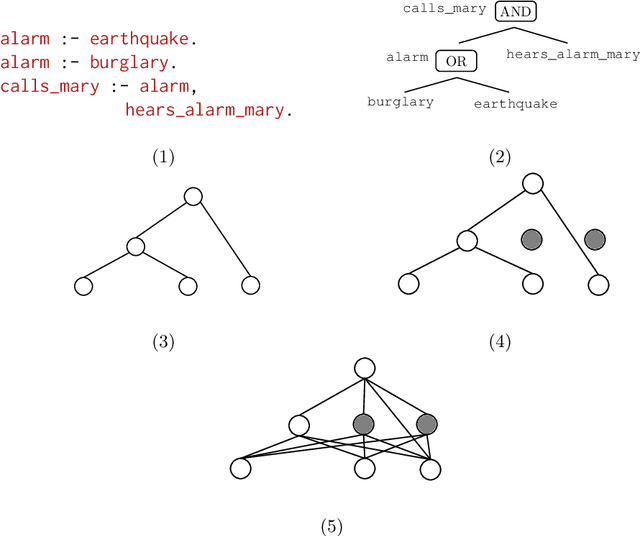
Abstract:Neural-symbolic and statistical relational artificial intelligence both integrate frameworks for learning with logical reasoning. This survey identifies several parallels across seven different dimensions between these two fields. These cannot only be used to characterize and position neural-symbolic artificial intelligence approaches but also to identify a number of directions for further research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge