Semirings for Probabilistic and Neuro-Symbolic Logic Programming
Paper and Code
Feb 21, 2024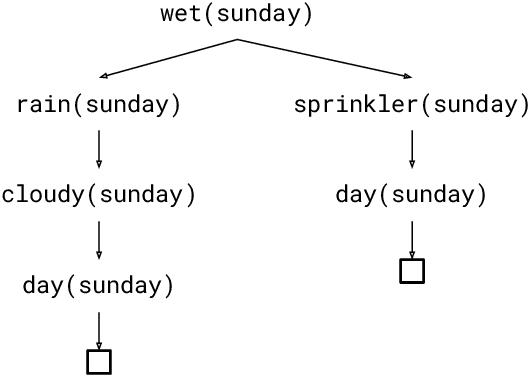

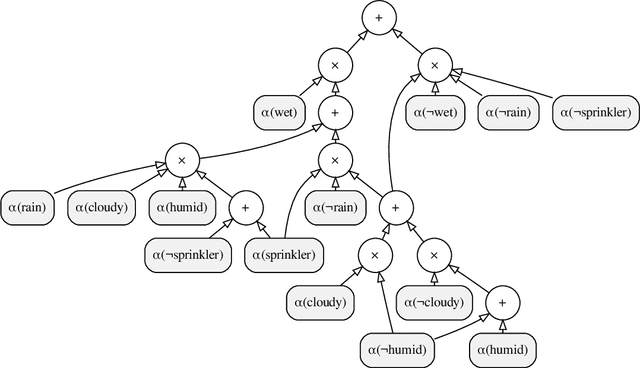
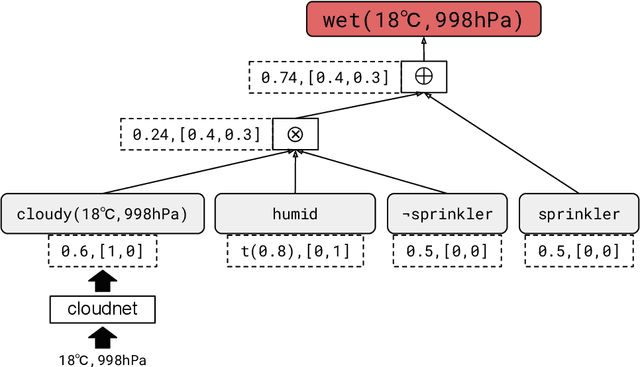
The field of probabilistic logic programming (PLP) focuses on integrating probabilistic models into programming languages based on logic. Over the past 30 years, numerous languages and frameworks have been developed for modeling, inference and learning in probabilistic logic programs. While originally PLP focused on discrete probability, more recent approaches have incorporated continuous distributions as well as neural networks, effectively yielding neural-symbolic methods. We provide a unified algebraic perspective on PLP, showing that many if not most of the extensions of PLP can be cast within a common algebraic logic programming framework, in which facts are labeled with elements of a semiring and disjunction and conjunction are replaced by addition and multiplication. This does not only hold for the PLP variations itself but also for the underlying execution mechanism that is based on (algebraic) model counting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge