KLay: Accelerating Neurosymbolic AI

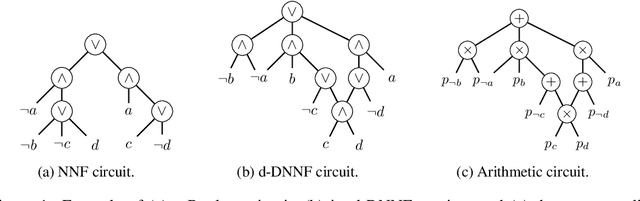
A popular approach to neurosymbolic AI involves mapping logic formulas to arithmetic circuits (computation graphs consisting of sums and products) and passing the outputs of a neural network through these circuits. This approach enforces symbolic constraints onto a neural network in a principled and end-to-end differentiable way. Unfortunately, arithmetic circuits are challenging to run on modern AI accelerators as they exhibit a high degree of irregular sparsity. To address this limitation, we introduce knowledge layers (KLay), a new data structure to represent arithmetic circuits that can be efficiently parallelized on GPUs. Moreover, we contribute two algorithms used in the translation of traditional circuit representations to KLay and a further algorithm that exploits parallelization opportunities during circuit evaluations. We empirically show that KLay achieves speedups of multiple orders of magnitude over the state of the art, thereby paving the way towards scaling neurosymbolic AI to larger real-world applications.

Pruning Boolean d-DNNF Circuits Through Tseitin-Awareness

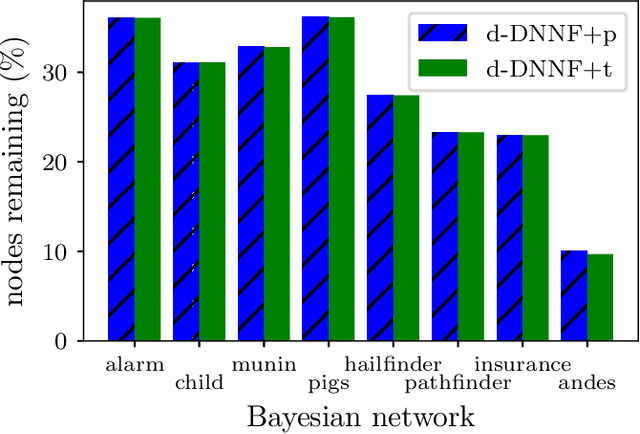
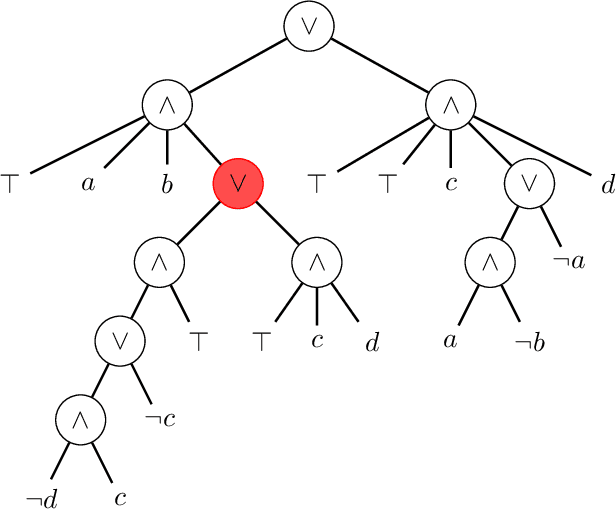
Boolean circuits in d-DNNF form enable tractable probabilistic inference. However, as a key insight of this work, we show that commonly used d-DNNF compilation approaches introduce irrelevant subcircuits. We call these subcircuits Tseitin artifacts, as they are introduced due to the Tseitin transformation step -- a well-established procedure to transform any circuit into the CNF format required by several d-DNNF knowledge compilers. We discuss how to detect and remove both Tseitin variables and Tseitin artifacts, leading to more succinct circuits. We empirically observe an average size reduction of 77.5% when removing both Tseitin variables and artifacts. The additional pruning of Tseitin artifacts reduces the size by 22.2% on average. This significantly improves downstream tasks that benefit from a more succinct circuit, e.g., probabilistic inference tasks.

On the Hardness of Probabilistic Neurosymbolic Learning

The limitations of purely neural learning have sparked an interest in probabilistic neurosymbolic models, which combine neural networks with probabilistic logical reasoning. As these neurosymbolic models are trained with gradient descent, we study the complexity of differentiating probabilistic reasoning. We prove that although approximating these gradients is intractable in general, it becomes tractable during training. Furthermore, we introduce WeightME, an unbiased gradient estimator based on model sampling. Under mild assumptions, WeightME approximates the gradient with probabilistic guarantees using a logarithmic number of calls to a SAT solver. Lastly, we evaluate the necessity of these guarantees on the gradient. Our experiments indicate that the existing biased approximations indeed struggle to optimize even when exact solving is still feasible.

Semirings for Probabilistic and Neuro-Symbolic Logic Programming

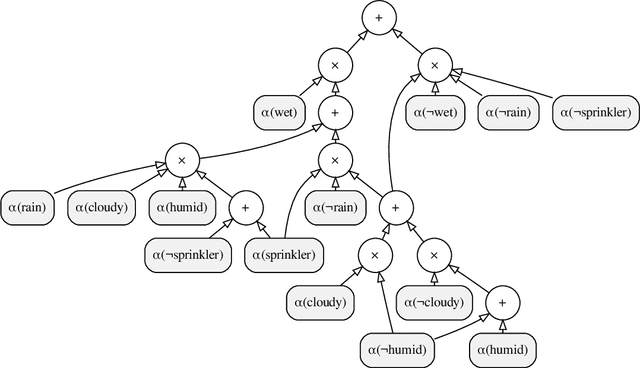
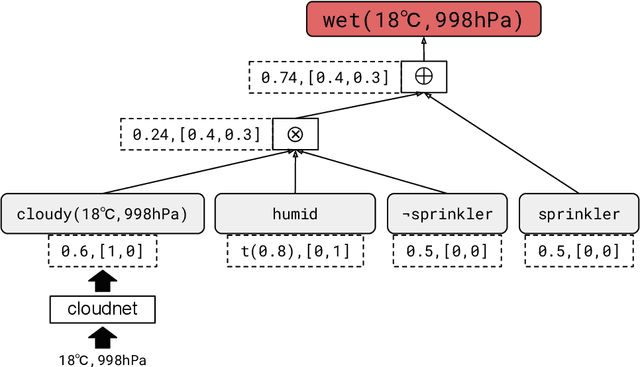
The field of probabilistic logic programming (PLP) focuses on integrating probabilistic models into programming languages based on logic. Over the past 30 years, numerous languages and frameworks have been developed for modeling, inference and learning in probabilistic logic programs. While originally PLP focused on discrete probability, more recent approaches have incorporated continuous distributions as well as neural networks, effectively yielding neural-symbolic methods. We provide a unified algebraic perspective on PLP, showing that many if not most of the extensions of PLP can be cast within a common algebraic logic programming framework, in which facts are labeled with elements of a semiring and disjunction and conjunction are replaced by addition and multiplication. This does not only hold for the PLP variations itself but also for the underlying execution mechanism that is based on (algebraic) model counting.

Top-Down Knowledge Compilation for Counting Modulo Theories

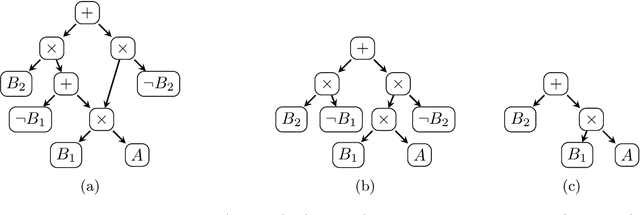
Propositional model counting (#SAT) can be solved efficiently when the input formula is in deterministic decomposable negation normal form (d-DNNF). Translating an arbitrary formula into a representation that allows inference tasks, such as counting, to be performed efficiently, is called knowledge compilation. Top-down knowledge compilation is a state-of-the-art technique for solving #SAT problems that leverages the traces of exhaustive DPLL search to obtain d-DNNF representations. While knowledge compilation is well studied for propositional approaches, knowledge compilation for the (quantifier free) counting modulo theory setting (#SMT) has been studied to a much lesser degree. In this paper, we discuss compilation strategies for #SMT. We specifically advocate for a top-down compiler based on the traces of exhaustive DPLL(T) search.