The Gradient of Algebraic Model Counting

Algebraic model counting unifies many inference tasks on logic formulas by exploiting semirings. Rather than focusing on inference, we consider learning, especially in statistical-relational and neurosymbolic AI, which combine logical, probabilistic and neural representations. Concretely, we show that the very same semiring perspective of algebraic model counting also applies to learning. This allows us to unify various learning algorithms by generalizing gradients and backpropagation to different semirings. Furthermore, we show how cancellation and ordering properties of a semiring can be exploited for more memory-efficient backpropagation. This allows us to obtain some interesting variations of state-of-the-art gradient-based optimisation methods for probabilistic logical models. We also discuss why algebraic model counting on tractable circuits does not lead to more efficient second-order optimization. Empirically, our algebraic backpropagation exhibits considerable speed-ups as compared to existing approaches.

KLay: Accelerating Neurosymbolic AI

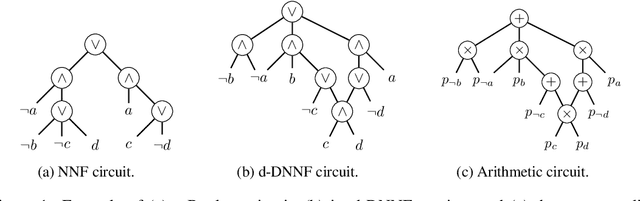
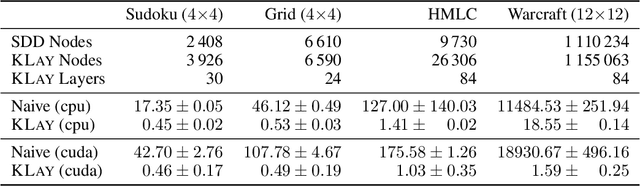
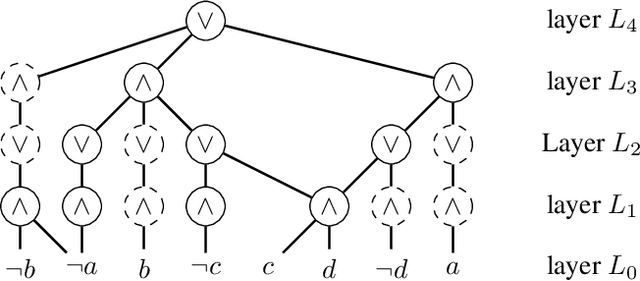
A popular approach to neurosymbolic AI involves mapping logic formulas to arithmetic circuits (computation graphs consisting of sums and products) and passing the outputs of a neural network through these circuits. This approach enforces symbolic constraints onto a neural network in a principled and end-to-end differentiable way. Unfortunately, arithmetic circuits are challenging to run on modern AI accelerators as they exhibit a high degree of irregular sparsity. To address this limitation, we introduce knowledge layers (KLay), a new data structure to represent arithmetic circuits that can be efficiently parallelized on GPUs. Moreover, we contribute two algorithms used in the translation of traditional circuit representations to KLay and a further algorithm that exploits parallelization opportunities during circuit evaluations. We empirically show that KLay achieves speedups of multiple orders of magnitude over the state of the art, thereby paving the way towards scaling neurosymbolic AI to larger real-world applications.

Extracting Finite State Machines from Transformers

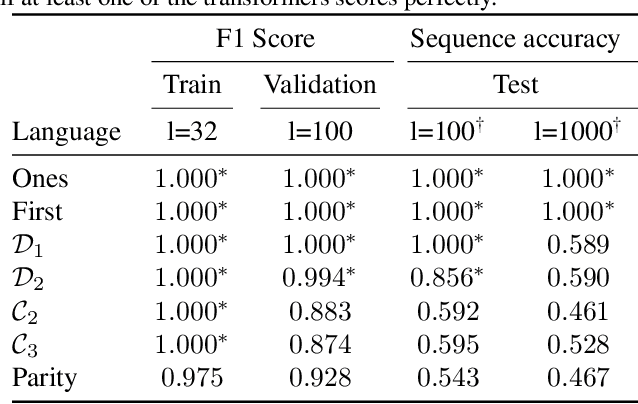
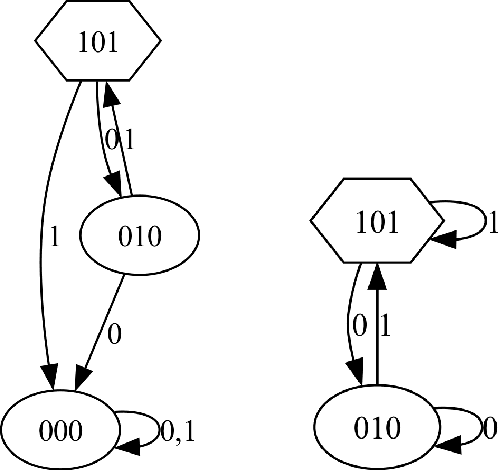
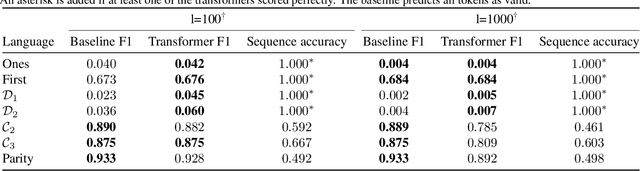
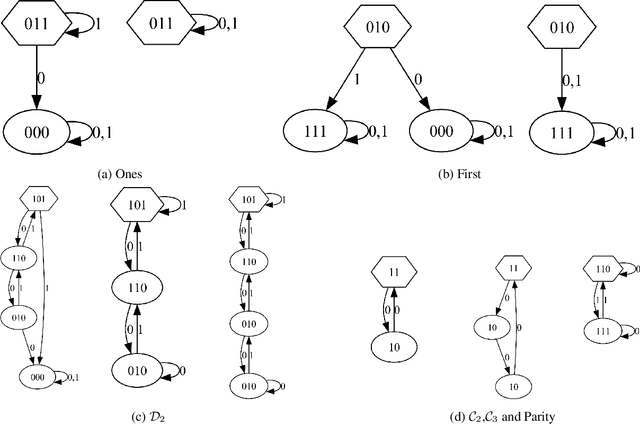
Fueled by the popularity of the transformer architecture in deep learning, several works have investigated what formal languages a transformer can learn. Nonetheless, existing results remain hard to compare and a fine-grained understanding of the trainability of transformers on regular languages is still lacking. We investigate transformers trained on regular languages from a mechanistic interpretability perspective. Using an extension of the $L^*$ algorithm, we extract Moore machines from transformers. We empirically find tighter lower bounds on the trainability of transformers, when a finite number of symbols determine the state. Additionally, our mechanistic insight allows us to characterise the regular languages a one-layer transformer can learn with good length generalisation. However, we also identify failure cases where the determining symbols get misrecognised due to saturation of the attention mechanism.

On the Hardness of Probabilistic Neurosymbolic Learning

The limitations of purely neural learning have sparked an interest in probabilistic neurosymbolic models, which combine neural networks with probabilistic logical reasoning. As these neurosymbolic models are trained with gradient descent, we study the complexity of differentiating probabilistic reasoning. We prove that although approximating these gradients is intractable in general, it becomes tractable during training. Furthermore, we introduce WeightME, an unbiased gradient estimator based on model sampling. Under mild assumptions, WeightME approximates the gradient with probabilistic guarantees using a logarithmic number of calls to a SAT solver. Lastly, we evaluate the necessity of these guarantees on the gradient. Our experiments indicate that the existing biased approximations indeed struggle to optimize even when exact solving is still feasible.

Towards Understanding Iterative Magnitude Pruning: Why Lottery Tickets Win

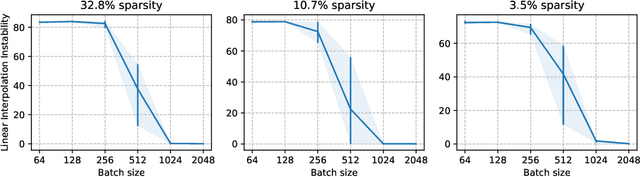
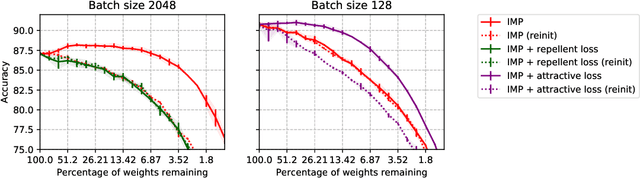
The lottery ticket hypothesis states that sparse subnetworks exist in randomly initialized dense networks that can be trained to the same accuracy as the dense network they reside in. However, the subsequent work has failed to replicate this on large-scale models and required rewinding to an early stable state instead of initialization. We show that by using a training method that is stable with respect to linear mode connectivity, large networks can also be entirely rewound to initialization. Our subsequent experiments on common vision tasks give strong credence to the hypothesis in Evci et al. (2020b) that lottery tickets simply retrain to the same regions (although not necessarily to the same basin). These results imply that existing lottery tickets could not have been found without the preceding dense training by iterative magnitude pruning, raising doubts about the use of the lottery ticket hypothesis.

NeurIPS 2020 NLC2CMD Competition: Translating Natural Language to Bash Commands

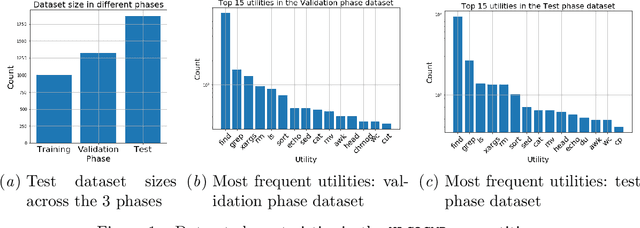
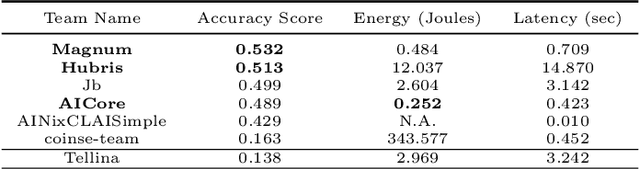
The NLC2CMD Competition hosted at NeurIPS 2020 aimed to bring the power of natural language processing to the command line. Participants were tasked with building models that can transform descriptions of command line tasks in English to their Bash syntax. This is a report on the competition with details of the task, metrics, data, attempted solutions, and lessons learned.