Towards Understanding Iterative Magnitude Pruning: Why Lottery Tickets Win

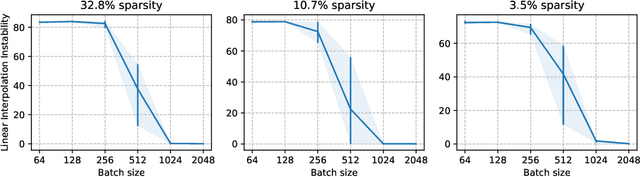
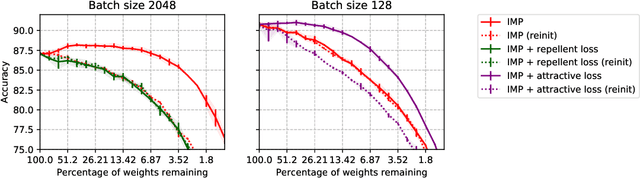
The lottery ticket hypothesis states that sparse subnetworks exist in randomly initialized dense networks that can be trained to the same accuracy as the dense network they reside in. However, the subsequent work has failed to replicate this on large-scale models and required rewinding to an early stable state instead of initialization. We show that by using a training method that is stable with respect to linear mode connectivity, large networks can also be entirely rewound to initialization. Our subsequent experiments on common vision tasks give strong credence to the hypothesis in Evci et al. (2020b) that lottery tickets simply retrain to the same regions (although not necessarily to the same basin). These results imply that existing lottery tickets could not have been found without the preceding dense training by iterative magnitude pruning, raising doubts about the use of the lottery ticket hypothesis.