ProbLog4Fairness: A Neurosymbolic Approach to Modeling and Mitigating Bias

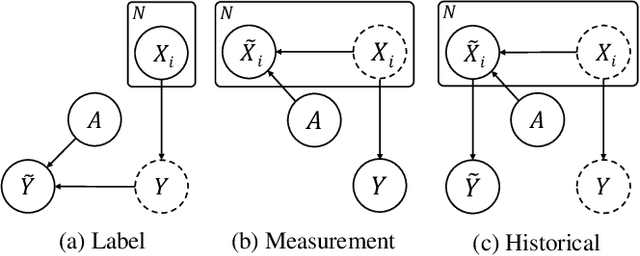
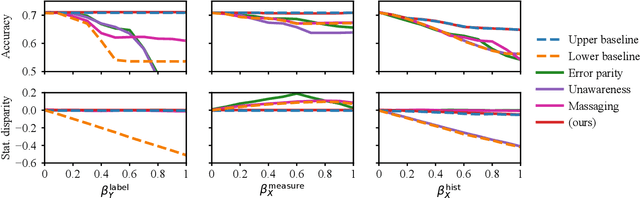
Operationalizing definitions of fairness is difficult in practice, as multiple definitions can be incompatible while each being arguably desirable. Instead, it may be easier to directly describe algorithmic bias through ad-hoc assumptions specific to a particular real-world task, e.g., based on background information on systemic biases in its context. Such assumptions can, in turn, be used to mitigate this bias during training. Yet, a framework for incorporating such assumptions that is simultaneously principled, flexible, and interpretable is currently lacking. Our approach is to formalize bias assumptions as programs in ProbLog, a probabilistic logic programming language that allows for the description of probabilistic causal relationships through logic. Neurosymbolic extensions of ProbLog then allow for easy integration of these assumptions in a neural network's training process. We propose a set of templates to express different types of bias and show the versatility of our approach on synthetic tabular datasets with known biases. Using estimates of the bias distortions present, we also succeed in mitigating algorithmic bias in real-world tabular and image data. We conclude that ProbLog4Fairness outperforms baselines due to its ability to flexibly model the relevant bias assumptions, where other methods typically uphold a fixed bias type or notion of fairness.

Extracting Finite State Machines from Transformers

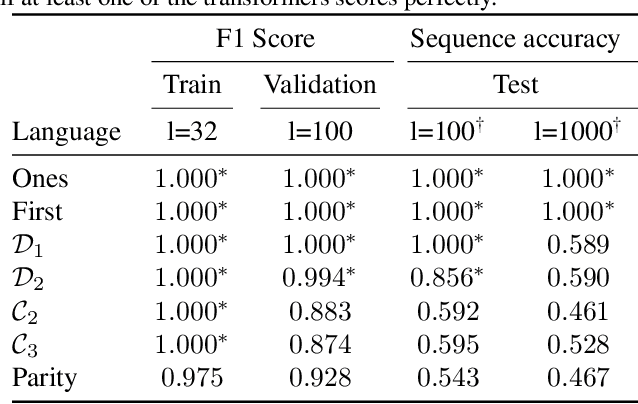
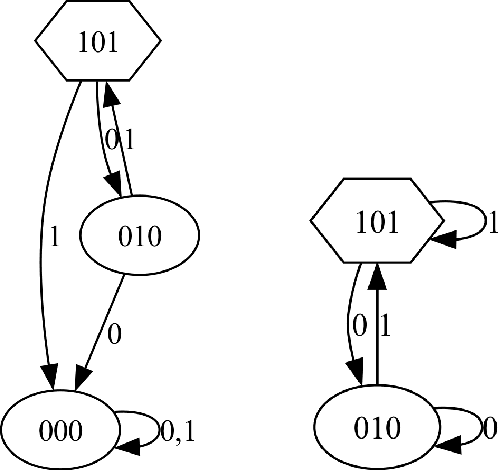
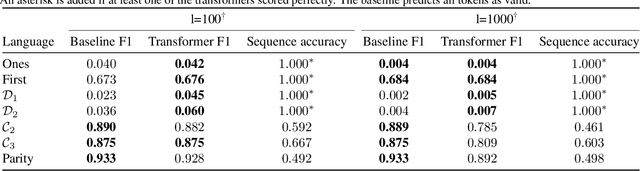
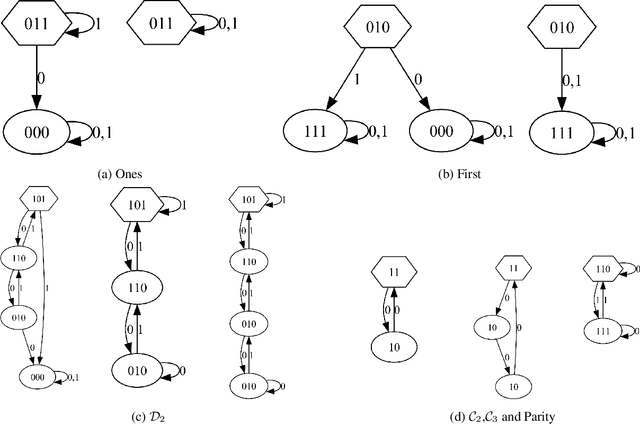
Fueled by the popularity of the transformer architecture in deep learning, several works have investigated what formal languages a transformer can learn. Nonetheless, existing results remain hard to compare and a fine-grained understanding of the trainability of transformers on regular languages is still lacking. We investigate transformers trained on regular languages from a mechanistic interpretability perspective. Using an extension of the $L^*$ algorithm, we extract Moore machines from transformers. We empirically find tighter lower bounds on the trainability of transformers, when a finite number of symbols determine the state. Additionally, our mechanistic insight allows us to characterise the regular languages a one-layer transformer can learn with good length generalisation. However, we also identify failure cases where the determining symbols get misrecognised due to saturation of the attention mechanism.