Paolo Morettin
Symbol Grounding in Neuro-Symbolic AI: A Gentle Introduction to Reasoning Shortcuts
Oct 16, 2025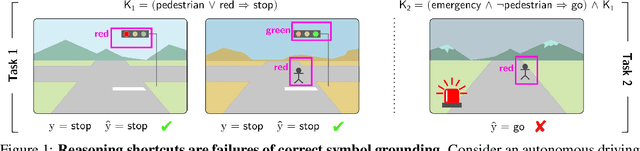

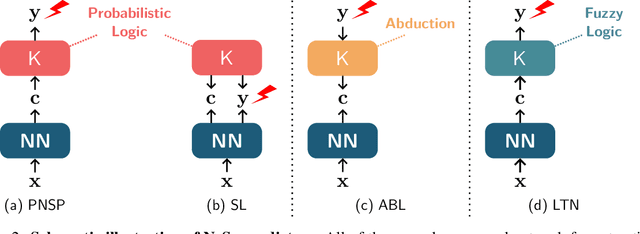
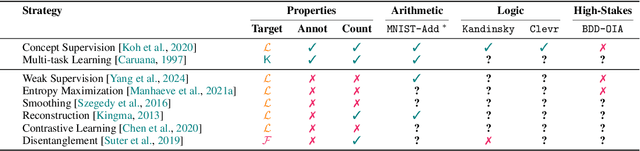
Abstract:Neuro-symbolic (NeSy) AI aims to develop deep neural networks whose predictions comply with prior knowledge encoding, e.g. safety or structural constraints. As such, it represents one of the most promising avenues for reliable and trustworthy AI. The core idea behind NeSy AI is to combine neural and symbolic steps: neural networks are typically responsible for mapping low-level inputs into high-level symbolic concepts, while symbolic reasoning infers predictions compatible with the extracted concepts and the prior knowledge. Despite their promise, it was recently shown that - whenever the concepts are not supervised directly - NeSy models can be affected by Reasoning Shortcuts (RSs). That is, they can achieve high label accuracy by grounding the concepts incorrectly. RSs can compromise the interpretability of the model's explanations, performance in out-of-distribution scenarios, and therefore reliability. At the same time, RSs are difficult to detect and prevent unless concept supervision is available, which is typically not the case. However, the literature on RSs is scattered, making it difficult for researchers and practitioners to understand and tackle this challenging problem. This overview addresses this issue by providing a gentle introduction to RSs, discussing their causes and consequences in intuitive terms. It also reviews and elucidates existing theoretical characterizations of this phenomenon. Finally, it details methods for dealing with RSs, including mitigation and awareness strategies, and maps their benefits and limitations. By reformulating advanced material in a digestible form, this overview aims to provide a unifying perspective on RSs to lower the bar to entry for tackling them. Ultimately, we hope this overview contributes to the development of reliable NeSy and trustworthy AI models.
A Probabilistic Neuro-symbolic Layer for Algebraic Constraint Satisfaction
Mar 25, 2025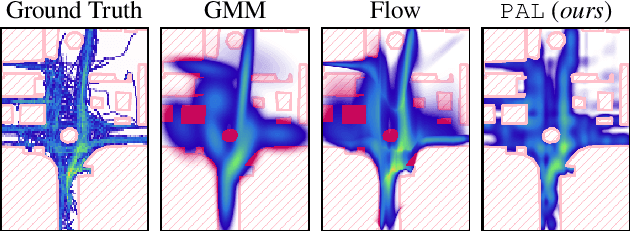
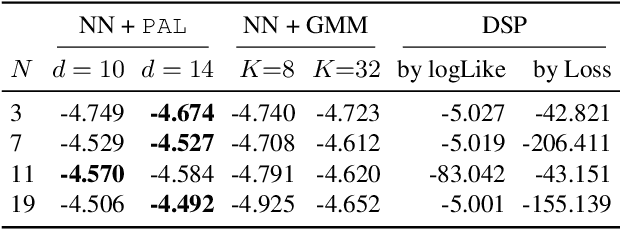
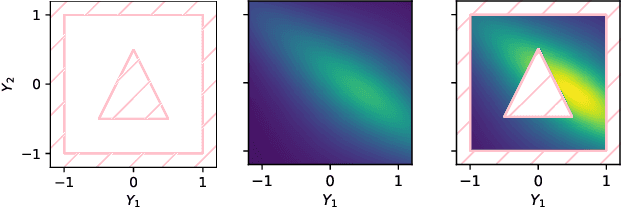
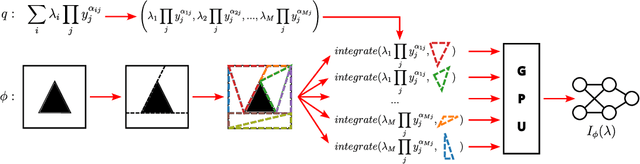
Abstract:In safety-critical applications, guaranteeing the satisfaction of constraints over continuous environments is crucial, e.g., an autonomous agent should never crash into obstacles or go off-road. Neural models struggle in the presence of these constraints, especially when they involve intricate algebraic relationships. To address this, we introduce a differentiable probabilistic layer that guarantees the satisfaction of non-convex algebraic constraints over continuous variables. This probabilistic algebraic layer (PAL) can be seamlessly plugged into any neural architecture and trained via maximum likelihood without requiring approximations. PAL defines a distribution over conjunctions and disjunctions of linear inequalities, parameterized by polynomials. This formulation enables efficient and exact renormalization via symbolic integration, which can be amortized across different data points and easily parallelized on a GPU. We showcase PAL and our integration scheme on a number of benchmarks for algebraic constraint integration and on real-world trajectory data.
A Benchmark Suite for Systematically Evaluating Reasoning Shortcuts
Jun 14, 2024



Abstract:The advent of powerful neural classifiers has increased interest in problems that require both learning and reasoning. These problems are critical for understanding important properties of models, such as trustworthiness, generalization, interpretability, and compliance to safety and structural constraints. However, recent research observed that tasks requiring both learning and reasoning on background knowledge often suffer from reasoning shortcuts (RSs): predictors can solve the downstream reasoning task without associating the correct concepts to the high-dimensional data. To address this issue, we introduce rsbench, a comprehensive benchmark suite designed to systematically evaluate the impact of RSs on models by providing easy access to highly customizable tasks affected by RSs. Furthermore, rsbench implements common metrics for evaluating concept quality and introduces novel formal verification procedures for assessing the presence of RSs in learning tasks. Using rsbench, we highlight that obtaining high quality concepts in both purely neural and neuro-symbolic models is a far-from-solved problem. rsbench is available at: https://unitn-sml.github.io/rsbench.
Semantic Loss Functions for Neuro-Symbolic Structured Prediction
May 12, 2024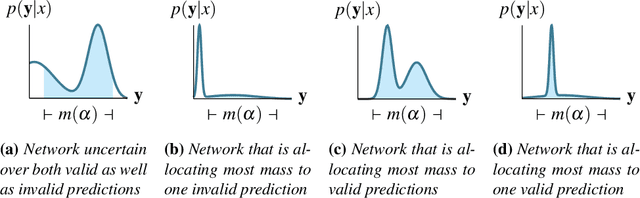
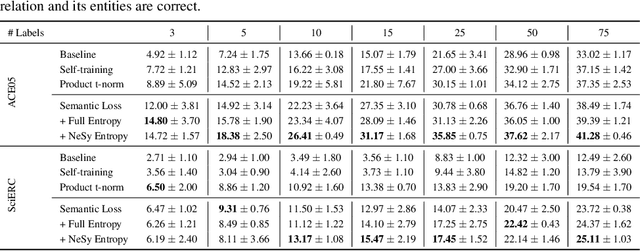
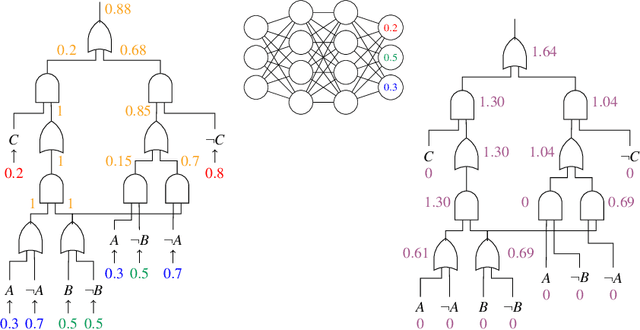
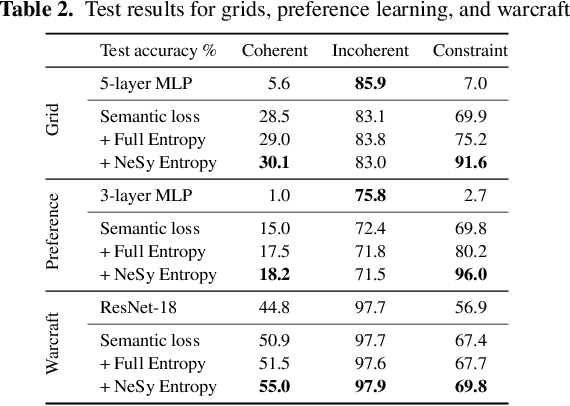
Abstract:Structured output prediction problems are ubiquitous in machine learning. The prominent approach leverages neural networks as powerful feature extractors, otherwise assuming the independence of the outputs. These outputs, however, jointly encode an object, e.g. a path in a graph, and are therefore related through the structure underlying the output space. We discuss the semantic loss, which injects knowledge about such structure, defined symbolically, into training by minimizing the network's violation of such dependencies, steering the network towards predicting distributions satisfying the underlying structure. At the same time, it is agnostic to the arrangement of the symbols, and depends only on the semantics expressed thereby, while also enabling efficient end-to-end training and inference. We also discuss key improvements and applications of the semantic loss. One limitations of the semantic loss is that it does not exploit the association of every data point with certain features certifying its membership in a target class. We should therefore prefer minimum-entropy distributions over valid structures, which we obtain by additionally minimizing the neuro-symbolic entropy. We empirically demonstrate the benefits of this more refined formulation. Moreover, the semantic loss is designed to be modular and can be combined with both discriminative and generative neural models. This is illustrated by integrating it into generative adversarial networks, yielding constrained adversarial networks, a novel class of deep generative models able to efficiently synthesize complex objects obeying the structure of the underlying domain.
A Unified Framework for Probabilistic Verification of AI Systems via Weighted Model Integration
Feb 07, 2024

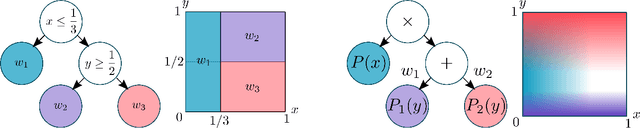
Abstract:The probabilistic formal verification (PFV) of AI systems is in its infancy. So far, approaches have been limited to ad-hoc algorithms for specific classes of models and/or properties. We propose a unifying framework for the PFV of AI systems based onWeighted Model Integration (WMI), which allows to frame the problem in very general terms. Crucially, this reduction enables the verification of many properties of interest, like fairness, robustness or monotonicity, over a wide range of machine learning models, without making strong distributional assumptions. We support the generality of the approach by solving multiple verification tasks with a single, off-the-shelf WMI solver, then discuss the scalability challenges and research directions related to this promising framework.
Top-Down Knowledge Compilation for Counting Modulo Theories
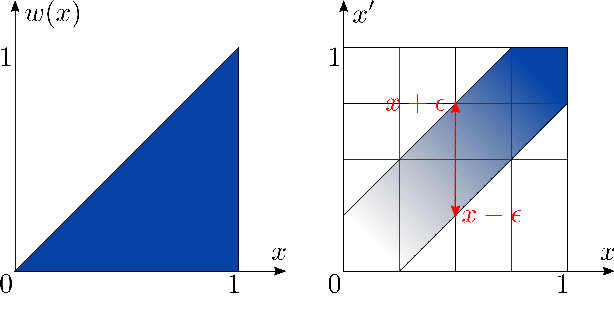
Jun 07, 2023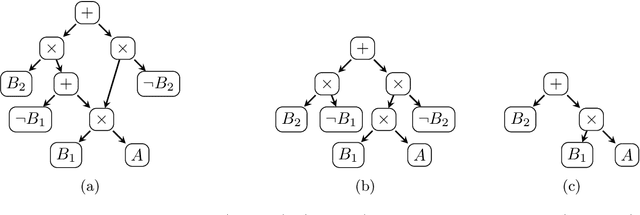
Abstract:Propositional model counting (#SAT) can be solved efficiently when the input formula is in deterministic decomposable negation normal form (d-DNNF). Translating an arbitrary formula into a representation that allows inference tasks, such as counting, to be performed efficiently, is called knowledge compilation. Top-down knowledge compilation is a state-of-the-art technique for solving #SAT problems that leverages the traces of exhaustive DPLL search to obtain d-DNNF representations. While knowledge compilation is well studied for propositional approaches, knowledge compilation for the (quantifier free) counting modulo theory setting (#SMT) has been studied to a much lesser degree. In this paper, we discuss compilation strategies for #SMT. We specifically advocate for a top-down compiler based on the traces of exhaustive DPLL(T) search.
Enhancing SMT-based Weighted Model Integration by Structure Awareness
Feb 13, 2023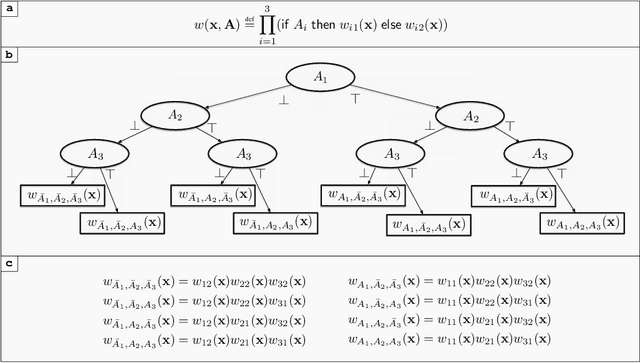

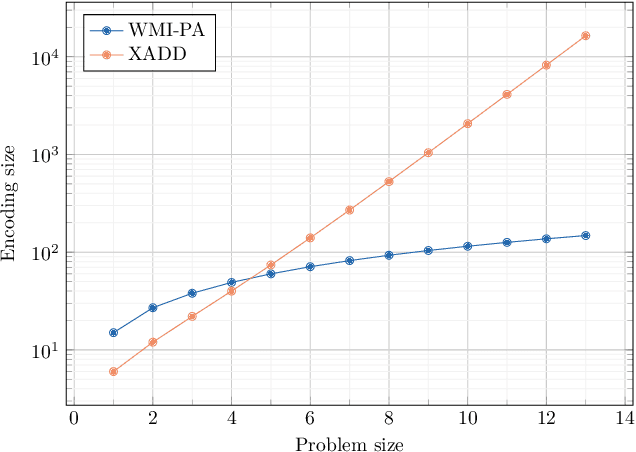
Abstract:The development of efficient exact and approximate algorithms for probabilistic inference is a long-standing goal of artificial intelligence research. Whereas substantial progress has been made in dealing with purely discrete or purely continuous domains, adapting the developed solutions to tackle hybrid domains, characterised by discrete and continuous variables and their relationships, is highly non-trivial. Weighted Model Integration (WMI) recently emerged as a unifying formalism for probabilistic inference in hybrid domains. Despite a considerable amount of recent work, allowing WMI algorithms to scale with the complexity of the hybrid problem is still a challenge. In this paper we highlight some substantial limitations of existing state-of-the-art solutions, and develop an algorithm that combines SMT-based enumeration, an efficient technique in formal verification, with an effective encoding of the problem structure. This allows our algorithm to avoid generating redundant models, resulting in drastic computational savings. Additionally, we show how SMT-based approaches can seamlessly deal with different integration techniques, both exact and approximate, significantly expanding the set of problems that can be tackled by WMI technology. An extensive experimental evaluation on both synthetic and real-world datasets confirms the substantial advantage of the proposed solution over existing alternatives. The application potential of this technology is further showcased on a prototypical task aimed at verifying the fairness of probabilistic programs.
SMT-based Weighted Model Integration with Structure Awareness
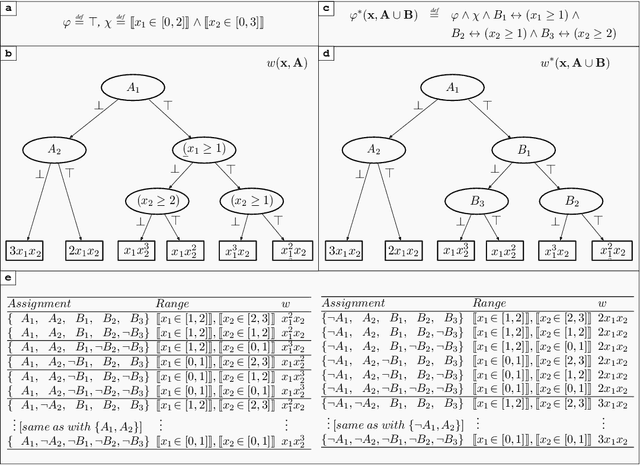
Jun 28, 2022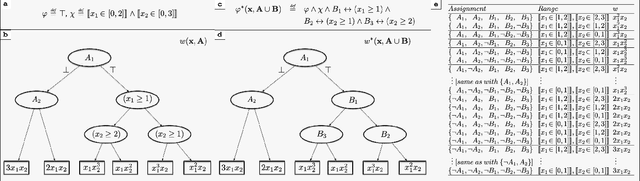
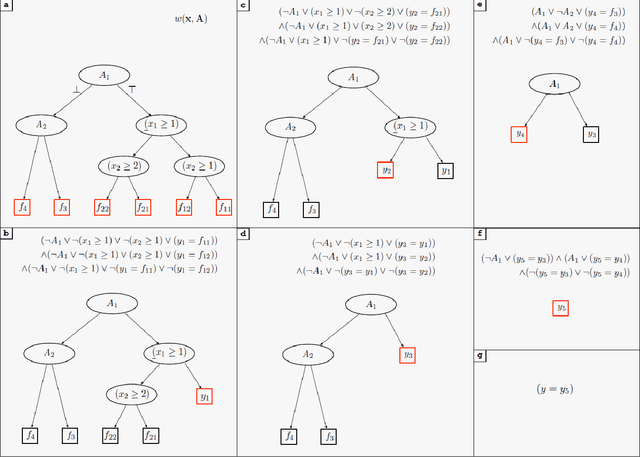


Abstract:Weighted Model Integration (WMI) is a popular formalism aimed at unifying approaches for probabilistic inference in hybrid domains, involving logical and algebraic constraints. Despite a considerable amount of recent work, allowing WMI algorithms to scale with the complexity of the hybrid problem is still a challenge. In this paper we highlight some substantial limitations of existing state-of-the-art solutions, and develop an algorithm that combines SMT-based enumeration, an efficient technique in formal verification, with an effective encoding of the problem structure. This allows our algorithm to avoid generating redundant models, resulting in substantial computational savings. An extensive experimental evaluation on both synthetic and real-world datasets confirms the advantage of the proposed solution over existing alternatives.
Efficient Generation of Structured Objects with Constrained Adversarial Networks
Jul 26, 2020


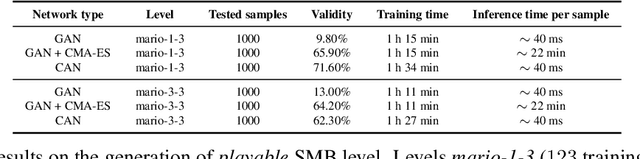
Abstract:Generative Adversarial Networks (GANs) struggle to generate structured objects like molecules and game maps. The issue is that structured objects must satisfy hard requirements (e.g., molecules must be chemically valid) that are difficult to acquire from examples alone. As a remedy, we propose Constrained Adversarial Networks (CANs), an extension of GANs in which the constraints are embedded into the model during training. This is achieved by penalizing the generator proportionally to the mass it allocates to invalid structures. In contrast to other generative models, CANs support efficient inference of valid structures (with high probability) and allows to turn on and off the learned constraints at inference time. CANs handle arbitrary logical constraints and leverage knowledge compilation techniques to efficiently evaluate the disagreement between the model and the constraints. Our setup is further extended to hybrid logical-neural constraints for capturing very complex constraints, like graph reachability. An extensive empirical analysis shows that CANs efficiently generate valid structures that are both high-quality and novel.
Scaling up Hybrid Probabilistic Inference with Logical and Arithmetic Constraints via Message Passing
Feb 28, 2020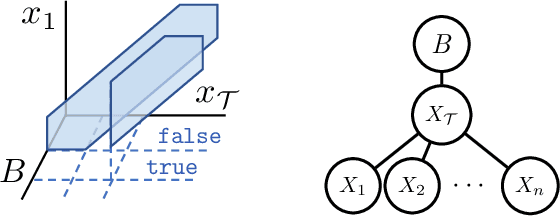
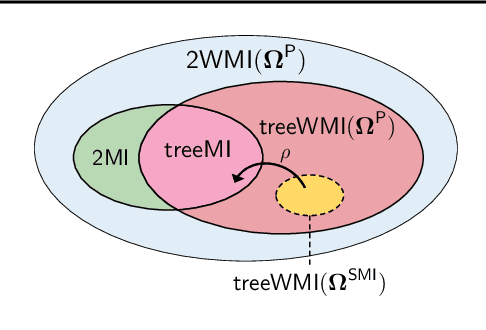
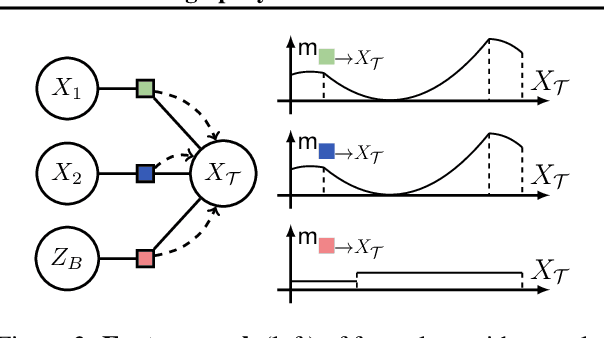
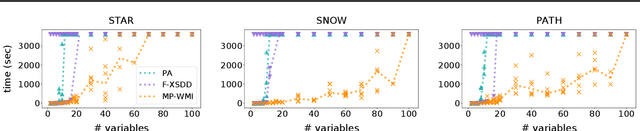
Abstract:Weighted model integration (WMI) is a very appealing framework for probabilistic inference: it allows to express the complex dependencies of real-world problems where variables are both continuous and discrete, via the language of Satisfiability Modulo Theories (SMT), as well as to compute probabilistic queries with complex logical and arithmetic constraints. Yet, existing WMI solvers are not ready to scale to these problems. They either ignore the intrinsic dependency structure of the problem at all, or they are limited to too restrictive structures. To narrow this gap, we derive a factorized formalism of WMI enabling us to devise a scalable WMI solver based on message passing, MP-WMI. Namely, MP-WMI is the first WMI solver which allows to: 1) perform exact inference on the full class of tree-structured WMI problems; 2) compute all marginal densities in linear time; 3) amortize inference inter query. Experimental results show that our solver dramatically outperforms the existing WMI solvers on a large set of benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge